14

Please help me to solve the following integral: $$\int_{-\pi/2}^{\pi/2} \frac{\sin^{2014}x}{\sin^{2014}x+\cos^{2014}x} dx$$ I have tried a lot, but no results. I only transformed this integral to the following also not easy integral: $$\int \frac{1}{(1+t^2)(1+t^{2014})} dt.$$

bahad
  • 141
  • 3
    Use the fact that $\sin(\frac{\pi}2-x)=\cos x$. – Macavity May 30 '15 at 16:59
  • 2
    ... or split the last integral over $[0,1]$ and $[1,+\infty)$, then apply the change of variable $t\to\frac{1}{s}$ in the second integral. – Jack D'Aurizio May 30 '15 at 17:04
  • Macavity, I don't understand what to do with $\sin(\pi/2-x)$? write in details please. – bahad May 30 '15 at 17:11
  • 1
    Jack D'Aurizio, I tried your change, it didn't help – bahad May 30 '15 at 17:11
  • 1
    Just a remark: I have used Mathematica to show that the function $F(a) = \int^{\pi/2}_{-\pi/2} \frac{\sin^a{x}}{\sin^a{x} + \cos^a{x}} , \mathrm{d}x$ has the following values: $F(0)=F(2)=F(4)=F(6)=F(8) = \pi/2$ and $F(1), \ F(3), , F(5)$ and $F(7)$ are not convergent in $(-\pi/2,\pi/2)$. Maybe you can compute easily what $F(2k)$ is. – Dmoreno May 30 '15 at 17:11
  • 1
    This boils down to this general integral: http://math.stackexchange.com/questions/605673/integrate-int-0-pi-2-frac11-tan-alphax-mathrmdx/605713#605713 – Ron Gordon May 30 '15 at 19:34

4 Answers4

15

Consider the integral \begin{align} I = \int_{-\pi/2}^{\pi/2} \frac{\sin^{2a}x}{\sin^{2a}x + \cos^{2a}x} \, dx. \end{align} This may also be seen as \begin{align} I &= \int_{0}^{\pi/2} \frac{\sin^{2a}x}{\sin^{2a}x + \cos^{2a}x} \, dx + \int_{-\pi/2}^{0} \frac{\sin^{2a}x}{\sin^{2a}x + \cos^{2a}x} \, dx \\ &= \int_{0}^{\pi/2} \frac{\sin^{2a}x}{\sin^{2a}x + \cos^{2a}x} \, dx - \int_{\pi/2}^{0} \frac{\sin^{2a}x}{\sin^{2a}x + \cos^{2a}x} \, dx \\ &= 2 \, \int_{0}^{\pi/2} \frac{\sin^{2a}x}{\sin^{2a}x + \cos^{2a}x} \, dx \end{align} where $x \to -x$ was made in the second integral. Now make the substitution $x = t-\pi/2$ to obtain \begin{align} I = 2 \, \int_{-\pi/2}^{0} \frac{\cos^{2a}t}{\sin^{2a}t + \cos^{2a}t} \, dt. \end{align} Now let $t \to -x$ to obtain \begin{align} I = 2 \, \int_{0}^{\pi/2} \frac{\cos^{2a}x}{\sin^{2a}x + \cos^{2a}x} \, dx. \end{align} Adding the two integral expressions leads to \begin{align} 2 I &= 2 \, \int_{0}^{\pi/2} \frac{\sin^{2a}x + \cos^{2a}x}{\sin^{2a}x + \cos^{2a}x} \, dx = 2 \, \int_{0}^{\pi/2} dx = \pi. \end{align} It can now be stated that \begin{align} \int_{-\pi/2}^{\pi/2} \frac{\sin^{2a}x}{\sin^{2a}x + \cos^{2a}x} \, dx = \frac{\pi}{2}. \end{align}

Leucippus
  • 26,329
  • You were way faster than me! Very nice, by the way. – Dmoreno May 30 '15 at 17:32
  • why $sin^{2a}(-x)=sin^{2a}(x)$, why is even function? – Lucas May 30 '15 at 17:52
  • 1
    $\sin^{2a}(-x) = (-1)^{2a} , \sin^{2a}(x) = \sin^{2a}(x)$ since $(-1)^{2m} = ((-1)^{2})^{m} = (1)^{m} = 1$ – Leucippus May 30 '15 at 17:58
  • what did you led to use this method? is a general method or just an inspiration? – Lucas May 30 '15 at 18:01
  • @Lucas Problems of this type sometimes show up in the Putnam exam, IMO, USAMO, and other exam competitions. Calculus books from the late 1800's to 1930's sometimes use problems of this type as examples. Outside of that it is just experience that often finds nice solutions. – Leucippus May 30 '15 at 18:31
  • Very nice answer. BTW, the several times that you did the substitution $;x\to -x;$ could have been saved since all the functions there are even, since cosine always, whereas sine is odd but it is squared , so ... +1 – Timbuc May 30 '15 at 19:05
  • @Leucippus I would really like to understand how, in your 3rd math line, you got that $\int_{-\pi/2}^0 = -\int_{\pi/2}^0$. – KeyC0de Feb 12 '17 at 20:54
5

Notice the following properties of limits, $$\color{blue}{\int_{-a}^{a}f(x)dx =2\int_{0}^{a}f(x)dx\quad \text{if} \quad f(-x)=f(x)}$$ $$\color{blue}{\int_{0}^{a}f(x)dx =\int_{0}^{a}f(a-x)dx}$$

Now, let $$I=\int_{-\pi/2}^{\pi/2}\frac{\sin^{2014}x}{\sin^{2014}x+\cos^{2014}x}dx$$ $$\implies I=2\int_{0}^{\pi/2}\frac{\sin^{2014}x}{\sin^{2014}x+\cos^{2014}x}dx\tag 1$$ Using secong property, we get $$I=2\int_{0}^{\pi/2}\frac{\sin^{2014}\left(\frac{\pi}{2}-x\right)}{\sin^{2014}\left(\frac{\pi}{2}-x\right)+\cos^{2014}\left(\frac{\pi}{2}-x\right)}dx$$

$$\implies I=2\int_{0}^{\pi/2}\frac{\cos^{2014}x}{\sin^{2014}x+\cos^{2014}x}dx\tag 2$$ Now, adding eq(1) & (2), we get $$2I=2\int_{0}^{\pi/2}\left(\frac{\sin^{2014}x}{\sin^{2014}x+\cos^{2014}x}+\frac{\cos^{2014}x}{\sin^{2014}x+\cos^{2014}x}\right)dx$$ $$\implies I=\int_{0}^{\pi/2}\left(\frac{\sin^{2014}x+\cos^{2014}x}{\sin^{2014}x+\cos^{2014}x}\right)dx$$ $$=\int_{0}^{\pi/2}1. dx=[x]_{0}^{\pi/2}=\left[\frac{\pi}{2}-0\right]=\color{blue}{\frac{\pi}{2}}$$

Harish Chandra Rajpoot
  • 37,450
3

Another point of view, just to point out what's going on with the integral:

Consider the integral written in the form:

$$I(2k) = \int^{\pi/2}_{-\pi/2} \frac{1}{1+\cot^{2k}{x}} \, \mathrm{d} x, $$ and look at what happens with the integrand as $k$ goes to $\infty$ (in your case, $k = 512$):

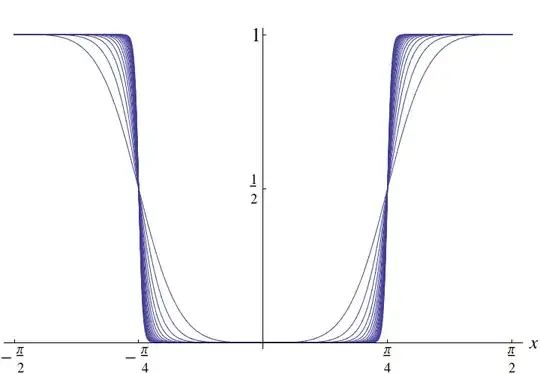
enter image description here

where I have ranged $k$ from $2$ to $20$. Can you infer an asymptotic behavior of $I(2k)$ as $k \to \infty$?

Cheers!

Edit: I was fascinated by the fact pointed out by @enzotib. In fact, this may suggest that $\partial I/\partial k = 0$. Let's compute the derivative of the integrand w.r.t. $k$:

$$ \frac{\partial}{\partial k} \frac{1}{1+\cot^{2k}{x}} = -\frac{2 \cot ^{2 k}(x) \log (\cot (x))}{\left(\cot ^{2 k}(x)+1\right)^2} =:f.$$ We observe that $f$ is only defined for $x > 0$ and, as a matter of fact, it's an odd function with respect the line $x = \pi/4$ for all $k$. Therefore, $F= \int^{\pi/2}_{-\pi/2} f \, \mathrm{d} x= 0$ for every $k$, meaning that $I$ does not depend on $k$. Since $F = \partial I / \partial k$, on integrating $F$ with respect to $k$, we can see that $I = c$, for some constant $c$. To determine the value of $c$, we plug any value of $k$ in $I$ to have that $I = I(0) = \int^{\pi/2}_{-\pi/2} \mathrm{d}x /2 = \pi/2$.

Dmoreno
  • 7,517
2

For $$ \int_a^{\pm(\pi/2-a)} \frac{\sin^{2a}x}{\sin^{2a}x + \cos^{2a}x} \, dx$$

I will use $$I=\int_p^q f(x)\ dx=\int_p^q f(p+q-x)\ dx$$

$$\implies I+I=\int_p^q [f(x)+ f(p+q-x)]\ dx$$

lab bhattacharjee
  • 274,582