10

If I were given $\lim_{n\to \infty}(1 + \frac{1}{n})^n$, and asked to solve, I would do so as follows:

$$\lim_{n\to \infty}(1 + \frac{1}{n})^n$$ $$=(1 + \frac{1}{\infty})^\infty$$ $$=(1 + 0)^\infty$$ $$=1^\infty$$ $$=1$$

I'm aware that this limit is meant to equal to $e$, and so I ask:

why don't I get $e$ when I solve $\lim_{n\to \infty}(1 + \frac{1}{n})^n$?

Martin Sleziak
  • 53,687
Cisplatin
  • 4,675
  • 7
  • 33
  • 58
  • 18
    To say it briefly: $1^\infty\neq 1$ – Yurii Savchuk Nov 03 '13 at 18:57
  • 15
    You can't just replace $n$ by $\infty$ and call it solving a limit. – Christoph Nov 03 '13 at 18:58
  • Presumably you meant to write $\lim_{n \to \infty}$, not $\lim_{x \to \infty}$. – Mike F Nov 03 '13 at 19:03
  • 12
    @OliverBel I find this a good question on the beginner's level. Lots of students find this type of limit calculations confusing/valid. The up votes perhaps reflect the fact that OP is not the only one finding this situation confusing. – Ittay Weiss Nov 03 '13 at 19:41
  • 5
    @OliverBel : maybe becaue the OP took the time to type his efforts in the question. – Stefan Smith Nov 03 '13 at 20:23
  • 2
    @OliverBel: I agree with Stefan Smith. Limits may be obvious to you, but they aren't to Sim, and his/her question makes it clear what he/she's tried and why he/she's confused. – Kevin Nov 03 '13 at 23:24
  • Euler defined the number $\large{\rm e}$ such that $\displaystyle{\large{{\rm d}{\rm e}^{x} \over {\rm d}x} = {\rm e}^{x},\ \forall\ x}$. Use this definition to find the limit. – Felix Marin Nov 04 '13 at 01:31

11 Answers11

20

The main problem here is that you use $\infty $ as if it were a number, and then you just substitute $\infty $ for $n$ and 'compute'. But, since infinity is not a number, you can't just substitute it and the computation you make is meaningless.

I'm assuming from the way you ask the question that you already know how to derive the correct value and that you are just wondering what is wrong with your approach. So, you don't get $e$ when you compute the limit they way you did precisely because your computation is invalid since you treat infinity as a number.

This may be extra confusing since sometimes substituting $\infty $ does lead to the correct answer, but this should be regarded as a fluke. For instance, the limit $\lim _{n\to \infty }\frac {1}{n}$ is $0$, which is what you would get by substituting $\infty $. But this is just coincidence that a completely faulty line of argument using entirely wrong 'computations' leads to the correct answer. Unfortunately, often when teaching calculus such substitutions and manipulations with $\infty $ are glossed over, or worse even encouraged. It is good practice to never ever substitute $\infty $ and compute with it.

Ittay Weiss
  • 79,840
  • 7
  • 141
  • 236
15

Consider $$\lim_{n\rightarrow \infty}(1+{1\over n})^n.$$ This limit has the indeterminate form $1^\infty$. Let $y=(1+{1\over n})^n$. Taking the natural logarithm of both sides of the equation and simplifying using the rules of logarithms we obtain $\ln(y)=n\ln(1+{1\over n})$. The $$\lim_{n\rightarrow \infty} \ln(y)=\lim_{n\rightarrow \infty}n\ln(1+{1\over n})$$ which has the indeterminate form $\infty\cdot 0$. We can rewrite the right-hand side limit as $$\lim_{n\rightarrow \infty}\ln(y)={\lim_{n\rightarrow \infty}={\ln(1+{1\over n})\over {1\over n}}}$$ which has the indeterminate form ${0\over 0}$. Using L'Hospital's Rule we see that $$\lim_{n\rightarrow \infty}\ln(y)=\lim_{n\rightarrow \infty}{{1\over (1+{1\over n})}\cdot {-1\over n^2}\over {-1\over n^2}}.$$ This simplifies to $$\lim_{n\rightarrow \infty} \ln(y)=\lim_{n\rightarrow \infty}(1+{1\over n})=1.$$ So far we have computed the limit of $\ln(y)$, what we really want is the limit of $y$. We know that $y=e^{\ln(y)}$. So $$\lim_{n\rightarrow \infty}(1+{1\over n})^n=\lim_{n\rightarrow \infty} y=\lim_{n\rightarrow \infty} e^{\ln(y)}=e^1=e.$$ Thus $$\lim_{n\rightarrow \infty} (1+{1\over n})^n=e.$$

1233dfv
  • 5,625
11

Hint : $1^\infty=(a^0)^\infty=a^{0\cdot\infty}=a^\text{Indeterminate}=\text{Indeterminate}$.

A more comprehensive list of such undetermined expressions can be found here.

Lucian
  • 48,334
  • 2
  • 83
  • 154
  • 1
    I would say that $1^\infty $ should be interpreted as $\lim _{n\to \infty }1^n$ (which is $1$) rather then as the indeterminate expression you came up with. – Ittay Weiss Nov 03 '13 at 19:33
  • $\lim_{n\to\infty}1^n=1$ . And $\lim_{n\to\infty}0\cdot n=0$ . But obviously this is not the case here, since $1+\frac1n\neq1\iff$ $\frac1n\neq0$ . – Lucian Nov 03 '13 at 19:44
  • 6
    The point is that the problem with OP's approach is not that $1^\infty $ is or is not $1$ (and I say, it is $1$). The problem is in the steps leading to the wrong conclusion that the limit OP is interested in is the same as $1^\infty$. The problem stems from substituting $\infty $ for $n$, a practice that should never be done. – Ittay Weiss Nov 03 '13 at 19:55
  • 2
    But it isn't... Pretty much for the same reason for which $0\cdot\infty$ cannot be reduced to the above mentioned case either, but is considered indeterminate. For instance, $1^\infty$ can also be viewed as $\lim_{n\to1}n^\infty$ , which can be either $0$ or $\infty$ , depending on how $n$ approaches the value $1$ . – Lucian Nov 03 '13 at 20:02
  • 2
    things like $\lim _{n\to \infty }n^\infty $ have no meaning at all. You seem to interpret the expression $1^\infty $ as the limit of something that tends to $1$ raised to the power of something that tends to $\infty $, and that of course is not uniquely defined. But a much more natural interpretation for $1^\infty $ is as the limit of $1$ raised to the power of something that tends to $\infty $, and that is simply $1$. Anyway, this is besides the point of OP's question, and is just a matter of how does one interpret $1^\infty $. – Ittay Weiss Nov 03 '13 at 20:05
  • But that's the whole point: the limit only exists if its value is unique, and beyond one's subjective interpretation. – Lucian Nov 03 '13 at 20:33
  • I've encountered this ‘unnatural’ interpretation when faced, for instance, with computing the value of the improper definite integral $\lim_{n\to\infty}\int_0^\infty e^{-x^n}dx$ , so it's not quite so abstract as you might be inclined to think. – Lucian Nov 03 '13 at 20:41
  • 1
    The point is that the interpretation and/or value of $1^\infty $ is only one fragment of where OP erred. The initial reduction of the limit OP was computing to the expression $1^\infty $ is where the problems start. Substituting $\infty $ and playing with it as if it were a number is a practice that should never be done. – Ittay Weiss Nov 03 '13 at 21:36
  • So you keep on saying, but generally speaking, that's not true. Take for instance $\lim_{n\to\infty}\sqrt[n]2=$$=\lim_{n\to\infty}2^\frac1n=2^\frac1\infty=2^0=1$. See here for further details. – Lucian Nov 03 '13 at 21:46
  • @Lucian: Yes, sometimes playing with $\infty$ and pretending it's a number will result in a correct answer, okay, sure. But getting the right answer most of the time does not make your steps mathematically valid. The symbol $\infty$ is not a real number, period. (Also, improper integrals $\int_0^\infty$ and infinite sums $\sum_{n=1}^\infty$ are defined by limits: $\int_0^\infty = \lim_{n\to\infty}\int_0^n$ and $\sum_1^\infty = \lim_{N\to\infty}\sum_1^N$.) – Jesse Madnick Nov 03 '13 at 21:51
  • Just because something is ‘not a number’ does not mean that all its operations are undefined. I'm sorry. – Lucian Nov 03 '13 at 21:56
  • You are free to extend any number system you want to include infinity, and then it's up to you to tell us exactly how your new number system behaves. In analysis it is convenient to sometime speak of the extended real numbers, that includes $\infty $, but never as a number system. The bottom line is that $\infty $ is not a number. It is not a real number, nor a complex number, nor any kind of number. Treating it as if it were a number is unjustified. The fact that sometimes when you do that you get correct results does not justify anything. – Ittay Weiss Nov 03 '13 at 22:10
  • Look, Mr. Weiss, with all due respect, I didn't make these rules. If I'm wrong, then so are all math teachers I've ever known, and all math books I've ever read. Nor did I or anyone else ever imply that ‘infinity is a number’. A matrix or a set isn't exactly a number either, but that doesn't stop us from ‘multiplying’ them, for instance. Nor are all operations which contain infinity undefined, but only some of them, and this for very logical reasons. – Lucian Nov 03 '13 at 22:21
  • @Lucian it is possible the books you encountered and/or the teachers who taught you are/were wrong. I don't know unless you point me to a book or teacher and then I can form a better opinion about the book or teacher. Aside, not everything that can be multiplied qualifies as a number system. Numbers are different than matrices or sets. Now, you say you 'didn't make these rules' and this is precisely the problem. Which rules are you referring to? How are you to manipulate this $\infty$ (be it a number or not)? which laws does it obey? – Ittay Weiss Nov 03 '13 at 22:34
  • Yes. It is, of course, “possible”.. :-) It's just not very likely, that's all.. :-) The undefined operations are the “negative” ones (- , $\div$ , log , $\sqrt{\ }$) that involve infinity on both sides, and the ones that can be reduced to them. This comes from the fact that $\infty\oplus(x>0)=\infty$ for all “positive” operations (+ , $\times$ , $\uparrow$, etc). For instance, $\frac00$ and $0\cdot\infty$ can both be shown to be equivalent with each other and with $\frac\infty\infty$ ; $1^\infty$ implies the former ; $\infty^0$ is the same as $\sqrt[\infty]\infty$ , and $0^0$ is its inverse. – Lucian Nov 03 '13 at 22:57
  • 1
    I've found an easier way to remember it as $\log(1^\infty) = \infty\log(1) = \infty 0$ (if it were determinate, then taking the log would preserve this). – asmeurer Nov 04 '13 at 01:20
  • @lucian notice that you just specified more cases where manipulations with $\infty$ are meaningless (you even claimed two such meaningless things are equivalent, whatever that may mean) than cases where such manipulations are meaningful. This only serves to show why we don't regard $\infty $ as a number. When you find yourself introducing something but then immediately giving a whole list of exceptions, one must wonder if it's useful at all. Most mathematician's seem to agree (and I certainly do) that $\infty$ should not be computed with as a number (but rather as the top element in a lattice) – Ittay Weiss Nov 04 '13 at 01:49
  • You lost me at lattice... :-) I also fail to understand your objection: the cases where operating with infinity is (quote/unquote) meaningful are infinite in number (e.g., $\pm\infty\pm x=\pm\infty$ , $\forall x\in\mathbb{R}$ or $\mathbb{C}$, and there are an infinity of real or complex numbers, of course. The same goes for $\frac x{\pm\infty}=0$, etc). You are the first and only person I've ever heard say such things. (Are these your own original / personal opinions, or perhaps that of a [sizeable] minority? Or is it the accepted / official / orthodox teaching in your country or insitution ?) – Lucian Nov 04 '13 at 04:05
  • The reference to lattices, without getting technical, is basically saying that you can add $\infty$ as a symbol to the real numbers and define it as the largest element. The only operations then that make sense are $x+\infty=\infty$ for all $x\in \mathbb R$, $x\cdot \infty=\infty$ for all $x>0$, and a few more. This is very rigorous and accepted and whoever uses it knows that this is a lattice theoretic concept, not a number theoretic one. What I'm objecting to is the practice, prevalent in many countries, of computing limits by substituting infinity. OP's question shows it is confusing. – Ittay Weiss Nov 04 '13 at 05:41
  • as for whether or not I'm in the minority, certainly among practicing mathematicians I am in the majority (I challenge you to show me a research article or advanced textbook that has in it expressions like $1^\infty$ or the like). When it comes to teaching, most analysis courses will do a proper job but most calculus courses probably resort to the sloppy $\frac{1}{\infty}=0$ business. When I teach calculus I tell all my students that any such computation will give them zero points immediately, they are not allowed to use $\infty$ that way in my classes, which may be more or less appreciated. – Ittay Weiss Nov 04 '13 at 05:48
  • Yes, that's what I had in mind. (My father knows these things better than me). But aren't these two identities equivalent to saying $\infty-\infty=x$ and $\frac\infty\infty=x$ , and therefore undetermined, since that x can be anything ? This seems to be the logical conclusion. Then, by abstract or symbolic manipulation, the rest of undefined / undecided / undetermined relations follow. And then, with these logically-deduced exceptions in place, the ‘sloppy’ system becomes coherent, self-consistent, and self-contained. In other words, rigorous. – Lucian Nov 04 '13 at 05:53
  • 1
    Such use of symbol $\infty$ only adds to more confusion. I have to agree with the viewpoint of Ittay Weiss. – Paramanand Singh Nov 04 '13 at 09:04
  • Perhaps the following sums up my objection. The computation of, e.g., $\lim_{x\to 2}\frac{1}{x}=\frac{1}{2}$ by substituting $x=2$ is an application of the theorem: if $f:\mathbb R\to \mathbb R$ is continuous, then $\lim {x\to a}f(x)=f(a)$. However, the computation $\lim{x\to \infty}\frac{1}{x}=0$ by substituting $x=\infty$ is not an application of said theorem, nor of any theorem in fact. It is a mnemonic for the theorem: if $f:\mathbb R\to \mathbb R$ is bounded, then $\lim_{x\to \infty }\frac{f(x)}{x}=0$. But, it is a bad mnemonic since it resembles something it is not, and so is confusing – Ittay Weiss Nov 04 '13 at 10:20
  • @IttayWeiss: The slogan that $1^\infty$ is indeterminate is widely used in calculus textbooks. I use it myself when teaching calculus. It is short for the statement that $\lim_{x\to c} f(x)^{g(x)}$ is indeterminate if $\lim_{x\to c}f(x)=1$ and $\lim_{x\to c}g(x)=\infty$. – Cheerful Parsnip Oct 23 '14 at 01:24
  • @GrumpyParsnip this long discussion is evidence for the confusion that using certain mnemonics can create. Treating the symbol $1$ for anything other than the number $1$ (in this context of real analysis) is confusing. $1$ does not stand for "any function whose limit is $1$". Using the mnemonic "$1^\infty $ is indeterminate", while widely used, created confusion. Particularly in calculus courses, where often students substitute an understanding of what limits are in favor of a long list of tricks of how to compute limits, it is dangerous to reinforce this behavior. – Ittay Weiss Oct 23 '14 at 03:36
5

$1^{\infty}$ is an indeterminate form: the base is going to 1 which is trying to bring the expression to 1, but the exponent is going to $\infty$ which is trying to pull the expression off to $\infty$ as well. That there are these opposing forces is how I try to explain why some forms of limits are indeterminate but other forms (like $0^{\infty}=0$) aren't.

Francis Adams
  • 2,808
  • 3
    In the expression $1^\infty $, the base is fixed. – Ittay Weiss Nov 03 '13 at 19:34
  • @IttayWeiss But then how do you interpret $0^0$? Shouldn't both also be fixed? – N. S. Nov 03 '13 at 21:15
  • $0^0$ is simply undefined. And the expression $1^\infty $ is something that is open for interpretation since the use of $\infty$ implies a limit. But in $0^0$ there is no limit implied and the answer is not uniquely determined by either the rules of algebra or the rules of common sense and applicability. – Ittay Weiss Nov 03 '13 at 21:38
  • 1
    @IttayWeiss In most Calculus textbooks in North America, the convention is that any expression of the type $ \lim (f(x))^{g(x)} =a^b$ simply means that $\lim f(x)=a$ and $\lim g(x)=b$. Now, if $a^b$ makes sense as a number, the continuity of $x^y$ implies that this expression, understood in this conventional sense, is the same as the number $a^b$...... Note that $1^\infty$ makes sense with this convention, but it doesn't make sense in the standard sense..... Of course people not familiar with this convention might find other meanings for it, whcih could look or be more natural..... – N. S. Nov 03 '13 at 22:17
  • @IttayWeiss ... but IMO it is improbable for a student to start using notations like $1^\infty$ without seeing this convention, which is pretty standard in some places, before.... – N. S. Nov 03 '13 at 22:19
  • 2
    Since $\infty $ is not a number, expressions such as $1^\infty $ are vague expressions at best and should be avoided. I am aware of the practice, especially in calculus classes, to pretend that $\infty$ is a number and use all sorts of half-baked conventions. This is a bad practice. – Ittay Weiss Nov 03 '13 at 22:25
  • @IttayWeiss: Remembering that $1^\infty$ is indeterminate is much easier than remembering that $\lim_{x\to c} f(x)^{g(x)}$ is indeterminate if $\lim_{x\to x}f(x)=1$ and $\lim_{x\to c} g(x)=\infty$. It's a mnemonic for remembering not an algebraic expression. It's similar to how we say $\infty/\infty$ is indeterminate. It reminds us that if the numerator and denominator both limit to infinity, the the limit needs to be evaluated by some other means. – Cheerful Parsnip Oct 23 '14 at 01:29
  • @GrumpyParsnip if you like we can continue this in chat. We certainly don't need to run the discussion in two different answer threads... – Ittay Weiss Oct 23 '14 at 03:37
4

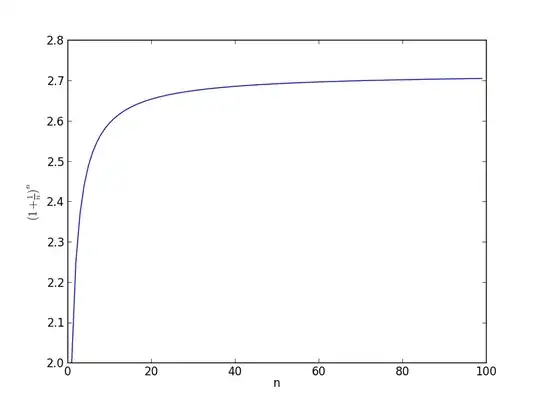
I think it's instructive to look at what happens as n grows. At the bottom of my answer I've attached a plot showing $(1 + \frac{1}{n})^n$ as a function of n from 1 to 100.

Hopefully this plot makes a little intuitive sense. Although as $n\to\infty$, $(1 + \frac{1}{n})$ gets very small, you are raising it to a higher and higher power.

For example, when $n = 10$:

$$1 + \frac{1}{10} = 1.1$$

which is pretty close to $1$, but!

$$1.1^{10} \approx 2.6$$

e as a limit

To answer your question: You cannot substitute the limiting value in the expression and get the proper limit. As an example, consider

$$f(x) = \frac{(x^2 - 1)}{x-1}$$

If we try to take the limit as $x \to 1$ by simply substituting $x = 1$, we get

$$\lim_{x \to 1}f(x) = \frac{1^2 - 1}{1 - 1} = \frac{0}{0}$$

whereas the true limit can be found by factoring the numerator:

$$f(x) = \frac{(x-1)(x+1)}{x-1} = x + 1$$

so:

$$\lim_{x \to 1}f(x) = 2$$

See the Wikipedia page on limits.

user545424
  • 160
  • 4
  • 2
  • you probably meant to say that $1+\frac{1}{n}$ gets very close to $1$, rather than say that it gets very small. 2) The example you give later is a bit problematic for the purposes of the question. The substitution you give fails because of the term $0/0$. But then you show the correct computation, where you can eventually substitute and get the right answer. The issue is that substitution to compute limits is a good technique, but while it may work (under the suitable conditions), it never applies to substituting $\infty$. $\infty $ is not a number.
    • – Ittay Weiss Nov 03 '13 at 21:42
  • @IttayWeiss, 1) Yes you are right; I just noticed that. 2) You raise a good point. I initially thought the major mistake was the substitution, but in fact it is a combination of the substitution and $\infty$. I guess the second example, although it doesn't clearly illuminate the poster's mistake, still goes to show that simple substitution does not always work. I think the method of plotting the result for increasing n is a very good way to visualize what is happening during the limiting process. – user545424 Nov 03 '13 at 21:53