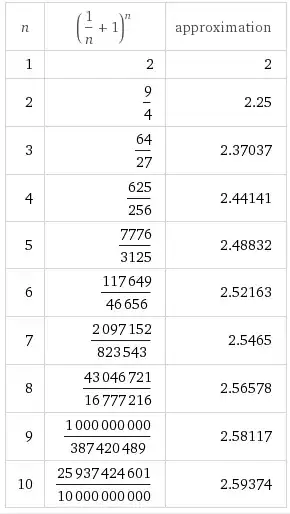
The number $e$ is characterized in calculus as:
$$e:=\lim_{n\to\infty}\left(1+\frac1n\right)^n$$
My question is this: As $n$ heads to infinity, $1/n$ gets closer and closer to zero. So what we're really doing is to add $1$ to a number that's getting closer and closer to zero and then raising that expression to an increasingly large number.
So, the limit as $n$ moves towards infinity is $1$. Why is it $e$?