Is there any equation for triangle?

Question

Like there's an equation of a circle, is there any equation of a triangle?

---

I've been trying to build one and the closest thing I've managed to do is to create an equation of 2 lines and use the $x$ axis as the 3rd side of the triangle.

Here's how I built the two lines equation:

Let $m$ be the slope of the first line, $-m$ is the slope of the second line, and $a$ is the x-value of their intersection point.

The first thing we need to do is to find the y-intercept of the second line. Let's call it $p$. The first line equation is $y=mx$ and the second line equation is $y=-mx+p$

$ma=-ma+p$

$p=2ma$

So we need to build an equation that equals to $y=mx+n$ when $x<a$ and to $y=-mx+2ma$ when $x>a$. First lets handle the slope. It should be $m$ when $x<a$ and $-m$ when $x>a$.

This can be achieved by:

$\dfrac {a-x} {|a-x|} m$

The y-intercept of the final equation should be $0$ when $x<a$ and $2ma$ when $x>a$.

This can be achieved by:

$(\dfrac {x-a} {|a-x|} + 1)*2ma$

So our equation looks like:

$y=\dfrac {a-x} {|a-x|} mx+(\dfrac {x-a} {|a-x|} + 1)*2ma$

Simplified:

$y=\dfrac {-m(x-a)^2} {|a-x|} + ma$

Or:

$y=m(x-a)sgn(a-x)+ma$

Plot $m=2, a=5$:

---

So is there any way to build an equation for triangle without using the $x$ axis as the 3rd side of the triangle?

Answer 1

If you really, really want a single equation that defines a triangle, you could make one by a trick such as

$$ \big(|x-a|+|x-b|-|a-b|\big) \big(|x-b|+|x-c|-|b-c|\big) \big(|x-c|+|x-a|-|c-a|\big)=0 $$

where $x$ is the unknown and $a, b, c$ are the corners of the triangle, all being vectors.

However, such an equation won't in particular help you understand the triangle, nor will it be very helpful for reasoning about it or calculating things about it. In just about every conceivable application, a different representation of the triangle than an equation will be more useful.

Answer 2

Some "closed" expressions for the triangle are quite useful, as is obvious from the following web page: Efficient 2-D & 3-D Point Probes.

The gist of the method is the so-called isoparametric ("same parameters") transformation, where "isoparametric" is a terminology which is quite common in Finite Element contexts. An elaborate explanation of it has been given, as an answer to the following MSE question: Converting triangles to isosceles, equilateral or right???

The formulas which express the local coordinates $\xi$ and $\eta$ into the global coordinates $x$ and $y$ are repeated here for convenience: $$ \begin{array}{ll} \xi = [ (y_3 - y_1).(x - x_1) - (x_3 - x_1).(y - y_1) ]/\Delta \\ \eta = [ (x_2 - x_1).(y - y_1) - (y_2 - y_1).(x - x_1) ]/\Delta \end{array} $$ Here $\Delta$ is the determinant of the inverse transformation.
With the above, the "closed" triangle equation $T(x,y) = 0$ is simply given with: $$ T(x,y) = \min( \xi , \eta , 1 - \xi - \eta )$$
The maximum of the function $T$ is reached for $\xi = \eta = 1 - \xi - \eta = 1/3$ , hence at the midpoint (barycenter) of the triangle. If we draw straight lines from the midpoint towards the vertices, and further, then the whole plane is subdivided into three regions, one where $T(x,y) = \xi$ , one where $T(x,y) = \eta$ and one where $ T(x,y) = 1 - \xi - \eta$ . Our "inside/outside" function $T$ is zero at the triangle sides, positive inside and negative outside. It's shaped like a mountain with top $1/3$ at the midpoint and three sharply edged slopes downhill. The contour lines of this function are triangles, where the contour line with height $0$ is the original triangle itself. ( Quite the same is the case with the equation of e.g. a circle: $C(x,y) = 0$ with $C(x,y) = R^2 - (x-a)^2 - (y-b)^2$. )

A generalization of the linear triangle in 2-D to a linear tetrahedron in 3-D is given in the following answer : Computing a three-dimensional Lebesgue measure of a bounded set .

Answer 3

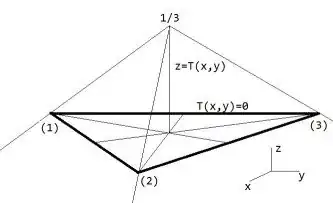
Okay, so I have an answer.

It's a very cheeky answer, which relies on a lot of technicalities, but to make a long story short, we're going to glue together a bunch of functions into a three-sided shape.

Before we get into what that's going to look like, I think you should see the glue. It relies on a few properties of zero. Namely:

• No two positive real nonzero numbers can be added to produce zero.
• Zero multiplied by any value results in zero.
• No two nonzero real numbers can be multiplied together to produce zero.

This gives us a pair of formulas which can in turn be evaluated almost like Boolean logic statements: $$ a*b = 0$$

This bakes a logical OR into our formula; you'll only get zero as the result if $a$ is zero or $b$ is zero. If both of them are real numbers with nonzero values, the result you get will also be nonzero. $$ |a|+|b| = 0$$

This bakes in a logical AND; you'll only get zero as the result if $a$ and $b$ are both zero. Note the use of absolute values; this ensures that $a$ and $b$ both have to be evaluated as positive numbers, and this formula wouldn't work without them, since it's entirely possible to have $a = -b$.

Finally, take note of the fact that standard formulas are either defined in terms of zero or are easily re-framed into terms of zero, which gives us some nice plug-and-play capabilities.

Overall, our formula will basically be this: $$AB*AC*BC=0$$

Or, in plain speak: "The point $(x,y)$ is a solution for triangle $ABC$ if it's a solution for line segment $AB$, line segment $AC$, or line segment $BC$."

The problem is, we don't have a standard equation for a line segment. We could conceivably make one if we pointed two rays at each other (such that all colinear points between their two points of origin are encompassed in a solution set), but we don't have a standard equation for rays either.

What we do have is some black magic:

$$ my (|x-2x_0|+x)/2 - mx (y + y_0 - x_0) = 0$$ $$ mx (|y-2y_0|+x)/2 - my (x + x_0 - y_0) = 0$$

Each of these equations produces a solution set which encompasses both a ray, originating from the point $(x_0, y_0)$ and travelling in the direction $(mx, my)$, and a second ray originating from the same point and travelling parallel to one of the axes (x-axis for the first formula, y-axis for the second). If you AND these two formulas together, you'll therefore get a ray. However, if you AND them together coming from opposite directions, you'll get a line segment instead, which means that while we could point two rays at each other by defining them individually, we can halve the size of our final formula by defining the line segments directly.

So then, for each segment, we get the following formulas: $$ AB : |((y_b - y_a) (|x-2x_a|+x)/2 - (x_b - x_a)(y + y_a - x_a))|+|((x_a - x_b) (|y-2y_b|+x)/2 - (y_a - y_b)(x + x_b - y_b))| = 0$$ $$ AC : |((y_c - y_a) (|x-2x_a|+x)/2 - (x_c - x_a)(y + y_a - x_a))|+|((x_a - x_c) (|y-2y_c|+x)/2 - (y_a - y_c)(x + x_c - y_c))| = 0$$ $$ BC : |((y_b - y_c) (|x-2x_c|+x)/2 - (x_b - x_a)(y + y_c - x_c))|+|((x_c - x_b) (|y-2y_b|+x)/2 - (y_c - y_b)(x + x_b - y_b))| = 0$$

Which gives us our final longform equation of (*inhales*):

$$ (|((y_b - y_a) (|x-2x_a|+x)/2 - (x_b - x_a)(y + y_a - x_a))|+|((x_a - x_b) (|y-2y_b|+x)/2 - (y_a - y_b)(x + x_b - y_b))|)*(|((y_c - y_a) (|x-2x_a|+x)/2 - (x_c - x_a)(y + y_a - x_a))|+|((x_a - x_c) (|y-2y_c|+x)/2 - (y_a - y_c)(x + x_c - y_c))|)*(|((y_b - y_c) (|x-2x_c|+x)/2 - (x_b - x_a)(y + y_c - x_c))|+|((x_c - x_b) (|y-2y_b|+x)/2 - (y_c - y_b)(x + x_b - y_b))|) = 0 $$

Now you have not only a means of condensing down any triangle into a singular equation, but also the method for putting together any polygon into such an equation, as well as any random collection of line segments, rays, or any other items for which you have a standard equation, so hopefully this was a useful answer, despite all the voodoo going on with the numbers.

However, as you can probably tell just by looking, this equation is horribly impractical for most applications, especially compared to most other methods. About the most use you'll get out of this is scaring the crap out of your classmates when you copy/paste a gigantic equation into Desmos and it spits out a pentagram with "HAIL SATAN" written under it.

Answer 4

The equation can be constructed as follows.

Suppose three linear equations define the sides of the triangle:

• $f_1(x,y)=0$
• $f_2(x,y)=0$
• $f_3(x,y)=0$

The functions can be written in two ways, differing by their signs. Example $x-y=0$ and $y-x=0$ both define the same line. For $f_1$, $f_2$ and $f_3$ we select the variant such that the center point (actually any point inside the triangle) is negative, i.e. $f_i(c_x, c_y)<0$.

The triangle equation is then: $$max(f1(x, y), f2(x, y), f3(x, y))=0$$

Because all $f_i$ are negative (by construction) inside, at least one $f_i$ has to be positive on the outside. The $max$ returns a positive number outside, a negative number inside, and therefore must be $0$ on the triangle itself.

Example:

The triangle with corners at $A=[-2,3]$, $B=[-4,-4]$ $C=[5,2]$ is bounded by the lines:

• $f1(x,y) = -19/7+x/7+y=0$
• $f2(x,y) = 2/3x-4/3-y=0$
• $f3(x,y) = -7/2x-10+y=0$

The triangle equation is: $$max(-19/7+x/7+y, 2/3x-4/3-y, -7/2x-10+y)=0$$

Plot:

https://www.desmos.com/calculator/wjdyovcwci

Answer 5

I see a lot of people overcomplicating this so I thought I'd offer something simpler.

If we imagine a triangle as a function using only the absolute value of $x$ and $y$, a simple triangle can be graphed with the equation:

$$ 1=\left\|y+\left|x\right|\right|+\left|x\right| $$

This equation produces a triangle that is symmetrical along the $y$ axis, and the maximum values of |$x$| and |$y$| are the same. However, we can adjust the position and parameter's of the triangle by modifying the first equation to:

$$ 1=\left|\frac{y}{a}-n+\left|\frac{x}{b}-m\right|\right|+\left|\frac{x}{b}-m\right| $$

Where $m$ and $n$ adjust the $x$ and $y$ position of the tringle, respectively. And $a$ and $b$ adjust the length and width of the triangle, respectively.

Here are both equations on Desmos

Note that a particular limitation of these equations is that they can only create symmetrical tringles.

Answer 6

There is no standard equation for a triangle, like there is for a circle, parabola or ellipse. The reason is that the circle for example has a clear classic geometric definition: A locus of points. It would be something like "The collection of points that have a fixed distance to a given point". From such a definition one would use the distance formula to arrive at an algebraic equation. The circle, ellipse, parabola and hyperbola all have such classic definitions (they are conic sections) and hence a set of standard equations. A triangle does not fall in that category at all. There is no classic definition for a "collection of points" that uniquely describes a triangle.

Answer 7

Triangle $A$ with points $x, y, z \in \Bbb{R}^2$ is the boundary of the convex set containing the points or the set of all $w = ax + by + cz, \ \ a + b + c = 1, \ a,b,c \geq 0$. Leting $S$ be that convex set, then $A = \partial S$, the boundary of $S$.

Answer 8

Building off of Alon Gubkin's formula, you can simply:

$am+m(-a+t)\text{sgn}(a-t) = m(a-\left|a-t\right|)$

assuming $a > 0$ and $m > 0$ and $t > 0$.

Answer 9

Dear friend If you want to make an triangle with vertices P1(x1, y1), P2(x2, y2) and P3(x3,y3) then the equation is given by,

0=max((y2-y3)(x-x3)/(x2-x3)+y3-y,y-(y2-y1)(x-x1)/(x2-x1)-y1,y-(y3-y1)(x-x1)/(x3-x1)-y1)

Provided x1≠x2 and x1≠x3 but x3 can be equal to x2.

Since I am not an expert in math.stackexchange.com I can't type it so effectively.

My first try. $$ 0 = \max \left( \frac{y2 - y3}{x2 - x3} (x - x3) + y3 - y , y - \frac{y2 - y1}{x2 - x1}(x - x1) - y1, y - \frac{y3 - y1}{x3 - x1}(x - x1) - y1 \right) $$ The only fault of this equation is that it cannot plot right angled triangles in which angle(P2)=90 or angle(P1)=90.

If you use x axis as the base and x1=x2/2, then x3=x2=0.

The equation is given by, $$ y= \frac{2y(-\frac{m(x-a)^2}{|x-a|} + ma )}{y+|y|} $$

Where $$ m = \frac{y3 - y1}{x3 - x1} $$ And a = x1.

The graph plots are given below:

https://www.desmos.com/calculator/d2ocynyzus

https://www.desmos.com/calculator/bfw2ufcq6e

For equilateral triangle : https://www.desmos.com/calculator/mjgqc6pigz

Thank you.