AfterMath. By "exclusively using integrals" has been done by Christian Blatter, so here comes the "like this in general" part, as formulated in the question too. Hope it is appreciated by the OP.
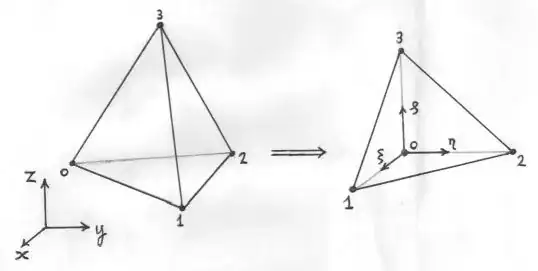
Linear Tetrahedron
Let's consider the simplest non-trivial finite element shape in 3-D, which is
a
linear tetrahedron. Function behaviour is approximated inside such a
tetrahedron by a
linear interpolation between the function values at the
vertices, also called nodal points. Let $T$ be such a function, and $x,y,z$
coordinates, then:
$$
T = A.x + B.y + C.z + D
$$
Where the constants A, B, C, D are yet to be determined.
Substitute $ x=x_k $ , $ y=y_k $ , $ z=z_k $ with $ k=0,1,2,3 $.
Start with:
$$
T_0 = A.x_0 + B.y_0 + C.z_0 + D
$$
Clearly, the first of these equations can already be used to eliminate the
constant $D$, once and forever:
$$
T - T_0 = A.(x - x_0) + B.(y - y_0) + C.(z - z_0)
$$
Then the constants $A$ , $B$ , $C$ are determined by:
$$ \begin{array}{ll}
T_1 - T_0 = A.(x_1 - x_0) + B.(y_1 - y_0) + C.(z_1 - z_0) \\
T_2 - T_0 = A.(x_2 - x_0) + B.(y_2 - y_0) + C.(z_2 - z_0) \\
T_3 - T_0 = A.(x_3 - x_0) + B.(y_3 - y_0) + C.(z_3 - z_0)
\end{array} $$
Three equations with three unknowns. A solution can be found:
$$
\left[ \begin{array}{c} A \\ B \\ C \end{array} \right] =
\left[ \begin{array}{ccc} x_1-x_0 & y_1-y_0 & z_1-z_0 \\
x_2-x_0 & y_2-y_0 & z_2-z_0 \\
x_3-x_0 & y_3-y_0 & z_3-z_0 \end{array} \right]^{-1}
\left[ \begin{array}{c} T_1-T_0 \\ T_2-T_0 \\ T_3-T_0 \end{array} \right]
$$
It is concluded that $A,B,C$ and hence $(T-T_0)$ must be a linear expression
in the $(T_k-T_0)$:
$$
T - T_0 = \xi.(T_1 - T_0) + \eta.(T_2 - T_0) + \zeta.(T_3 - T_0)
$$ $$ =
\left[ \begin{array}{ccc} \xi & \eta & \zeta \end{array} \right]
\left[ \begin{array}{c} T_1-T_0 \\ T_2-T_0 \\ T_3-T_0 \end{array} \right]
$$
See above:
$$ =
\left[ \begin{array}{ccc} \xi & \eta & \zeta \end{array} \right]
\left[ \begin{array}{ccc} x_1-x_0 & y_1-y_0 & z_1-z_0 \\
x_2-x_0 & y_2-y_0 & z_2-z_0 \\
x_3-x_0 & y_3-y_0 & z_3-z_0 \end{array} \right]
\left[ \begin{array}{c} A \\ B \\ C \end{array} \right]
$$
See above:
$$ = T - T_0 =
\left[ \begin{array}{ccc} x-x_0 & y-y_0 & z-z_0 \end{array} \right]
\left[ \begin{array}{c} A \\ B \\ C \end{array} \right]
$$
Hence:
$$ \begin{array}{ll}
x - x_0 = \xi .(x_1 - x_0) + \eta.(x_2 - x_0) + \zeta.(x_3 - x_0) \\
y - y_0 = \xi .(y_1 - y_0) + \eta.(y_2 - y_0) + \zeta.(y_3 - y_0) \\
z - z_0 = \xi .(z_1 - z_0) + \eta.(z_2 - z_0) + \zeta.(z_3 - z_0)
\end{array} $$
But also:
$$
T - T_0 = \xi.(T_1 - T_0) + \eta.(T_2 - T_0) + \zeta.(T_3 - T_0)
$$
Therefore the
same expression holds for the function $T$ as well as for
the coordinates $x,y,z$. This is called an
isoparametric transformation.
It is remarked without proof that the
local coordinates $\xi,\eta,\zeta$
within a tetrahedron can be interpreted as sub-volumes, spanned by the vectors
$ \vec{r}_k-\vec{r}_0 $ and $\vec{r}-\vec{r}_0 $ where $\vec{r}=(x,y,z) $ and
$k=1,2,3$. The general tetrahedron is thus mapped upon a special tetrahedron. This special tetrahedron is commonly called the
parent tetrahedron. It rests in $(\xi,\eta,\zeta)$ space and it has (unit) vertices $(0,0,0)$ , $(1,0,0)$ , $(0,1,0)$ , $(0,0,1)$ . The
inside ($\to$ volume) of both tetrahedrons is defined by:
$$
\xi > 0 \quad ; \quad \eta > 0 \quad ; \quad \zeta > 0 \quad ; \quad \xi + \eta + \zeta < 1
$$
Now for the volume of the general tetrahedron. It follows from the above that:
$$ \begin{array}{ll}
dx = (x_1 - x_0)\,d\xi + (x_2 - x_0)\,d\eta + (x_3 - x_0)\,d\zeta \\
dy = (y_1 - y_0)\,d\xi + (y_2 - y_0)\,d\eta + (y_3 - y_0)\,d\zeta \\
dz = (z_1 - z_0)\,d\xi + (z_2 - z_0)\,d\eta + (z_3 - z_0)\,d\zeta
\end{array} $$
Consequently:
$$
dx\,dy\,dz =
\begin{vmatrix} (x_1 - x_0) & (x_2 - x_0) & (x_3 - x_0) \\
(y_1 - y_0) & (y_2 - y_0) & (y_3 - y_0) \\
(z_1 - z_0) & (z_2 - z_0) & (z_3 - z_0) \end{vmatrix}
d\xi\,d\eta\,d\zeta
$$
Upon integration, we only have to calculate for the special case: the parent tetrahedron. Christian Blatter has shown how to do such a thing:
$$
\iiint d\xi\,d\eta\,d\zeta = \frac{1}{6}
$$
The general case follows from this:
$$
\iiint dx\,dy\,dz = \frac{1}{6}
\begin{vmatrix} (x_1 - x_0) & (x_2 - x_0) & (x_3 - x_0) \\
(y_1 - y_0) & (y_2 - y_0) & (y_3 - y_0) \\
(z_1 - z_0) & (z_2 - z_0) & (z_3 - z_0) \end{vmatrix}
$$
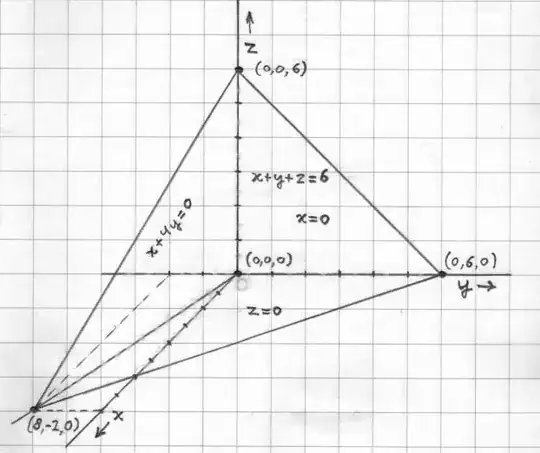
Let's work it out for the example at hand, where the vertices $(x_k,y_k,z_k)$ for
$\;k=0,1,2,3$ , upon (renewed) calculation, are given by: $(0,2,0)$, $(8,-2,0)$ ,
$(0,6,0)$ , $(0,2,4)$. So the volume is:
$$ \frac{1}{6}
\begin{vmatrix} (x_1 - x_0) & (x_2 - x_0) & (x_3 - x_0) \\
(y_1 - y_0) & (y_2 - y_0) & (y_3 - y_0) \\
(z_1 - z_0) & (z_2 - z_0) & (z_3 - z_0) \end{vmatrix}
= \frac{1}{6} \begin{vmatrix} 8 & 0 & 0 \\ -4 & 4 & 0 \\ 0 & 0 & 4 \end{vmatrix}
= \frac{64}{3}
$$
Further Notes. The theory of the linear tetrahedron is the 3-D generalization of
an analogous theory for the 2-D linear triangle:
As far as the latter reference is concerned, there exists a "closed" triangle equation in 2-D.
And there exists a "closed" tetraedron equation in 3-D as well:
$$
T(x,y,z) = \min( \xi , \eta , \zeta, 1 - \xi - \eta - \zeta )
$$
Our "inside/outside" function $T$ is zero at the boundaries of the tetrahedron, positive inside and negative outside. Quite the same is the case with more familiar closed 3-D equations, like the one of a sphere: $\;S(x,y,z) = R^2 - (x-a)^2 - (y-b)^2 - (z-c)^2$ .
The maximum of the function $T$ is reached for $\xi = \eta = \zeta = 1 - \xi - \eta - \zeta = 1/4$ , hence at the midpoint (barycenter) of the tetrahedron.