The subject presented here is some content of the Wikipedia page about
Platonic solids
combined with my own experience on Finite Elements.
To start with the
latter, there is a standard piece of Finite Element theory concerning
triangles on MSE.
The concept of isoparametrics is introduced herein. A reference to
the same theory is found in:
Is there any equation for triangle? (MSE).
So far so good for 2-D. In three dimensions the analogue of a triangle is
a tetrahedron. Let the parent tetrahedron have vertices (Finite Element
"nodes") that are numbered as follows:
$$
(0) = (0,0,0) \quad ; \quad (1) = (1,0,0) \quad ; \quad
(2) = (0,1,0) \quad ; \quad (3) = (0,0,1)
$$
Then any function with the parent tetrahedron can be interpolated as:
$$
f(\xi,\eta,\zeta) = (1-\xi-\eta-\zeta)f_0 + \xi\,f_1 + \eta\,f_2 + \zeta\,f_3
$$
Isoparametrics means that the same interpolation holds for the (global)
coordinates as well:
$$
x = (1-\xi-\eta-\zeta)x_0 + \xi \, x_1 + \eta \, x_2 + \zeta \, x_3 \\
y = (1-\xi-\eta-\zeta)y_0 + \xi \, y_1 + \eta \, y_2 + \zeta \, y_3 \\
z = (1-\xi-\eta-\zeta)z_0 + \xi \, z_1 + \eta \, z_2 + \zeta \, z_3
$$
From this the local parameters $(\xi,\eta,\zeta)$ can eventually be solved and
expressed in the global coordinates (which is not common practice, though).
Another frequently used Finite Element is the quadrilateral in 2-D or, quite analogously in 3-D: the hexahedron. The nodes of our parent element are: $$ (1) = (-1,-1,-1) \quad ; \quad (2) = (+1,-1,-1) \quad ; \quad (3) = (-1,+1,-1) \quad ; \quad (4) = (+1,+1,-1) \quad ; \quad (5) = (-1,-1,+1) \quad ; \quad (6) = (+1,-1,+1) \quad ; \quad (7) = (-1,+1,+1) \quad ; \quad (8) = (+1,+1,+1) $$ Then any function $h$ at the parent $h$exahedron can be interpolated as: $$ h(\xi,\eta,\zeta) = \frac{1}{8}(1-\xi)(1-\eta)(1-\zeta) h_1 + \frac{1}{8}(1+\xi)(1-\eta)(1-\zeta) h_2 + \frac{1}{8}(1-\xi)(1+\eta)(1-\zeta) h_3 + \frac{1}{8}(1+\xi)(1+\eta)(1-\zeta) h_4 + \frac{1}{8}(1-\xi)(1-\eta)(1+\zeta) h_5 + \frac{1}{8}(1+\xi)(1-\eta)(1+\zeta) h_6 + \frac{1}{8}(1-\xi)(1+\eta)(1+\zeta) h_7 + \frac{1}{8}(1+\xi)(1+\eta)(1+\zeta) h_8 $$ Note that this interpolation, in general, is not linear. And it's not so easy anymore to solve for the global coordinates ( by substituting $h = x,y,z$ ).
The following is a possible generalization of a finite element which was questioned about in: Understand 1D FEM solution using quadratics elements (MSE). In three dimensions we have the quite common Finite Difference Star, which is a not so common Finite Element, namely an octahedron augmented with the origin as an additional node $(0)$: $$ (0) = (0,0,0) \quad ; \quad (1) = (-1,0,0) \quad ; \quad (2) = (+1,0,0) \quad ; \quad (3) = (0,-1,0) \quad ; \quad (4) = (0,+1,0) \quad ; \quad (5) = (0,0,-1) \quad ; \quad (6) = (0,0,+1) $$ Then any function $s$ with the parent octahedron (F.D. $s$tar) can be interpolated as: $$ s(\xi,\eta,\zeta) = (1 - \xi^2 - \eta^2 - \zeta^2) s_0 + \frac{1}{2}\xi (\xi-1) s_1 + \frac{1}{2}\xi (\xi+1) s_2 + \frac{1}{2}\eta (\eta-1) s_3 + \frac{1}{2}\eta (\eta+1) s_4 + \frac{1}{2}\zeta (\zeta-1) s_5 + \frac{1}{2}\zeta (\zeta+1) s_6 $$ But now Wikipedia is consulted and the following is read in the chapter Dual polyhedra:
- The tetrahedron is self-dual (i.e. its dual is another tetrahedron).
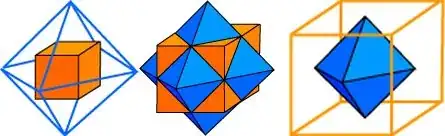
- The cube and the octahedron form a dual pair.
The other way around, we construct the dual of an arbitrary hexahedron, which is (not quite) an arbitrary octahedron: $$ s_1 = (h_1 + h_3 + h_5 + h_7)/4 \quad ; \quad s_2 = (h_2 + h_4 + h_6 + h_8)/4 \\ s_3 = (h_1 + h_2 + h_5 + h_6)/4 \quad ; \quad s_4 = (h_3 + h_4 + h_7 + h_8)/4 \\ s_5 = (h_1 + h_2 + h_3 + h_4)/4 \quad ; \quad s_6 = (h_5 + h_6 + h_7 + h_8)/4 \\ s_0 = (s_1 + s_2 + s_3 + s_4 + s_5 + s_6)/6 $$ Substitute this into the abovementioned expression for $s(\xi,\eta,\zeta)$ and simplify. The outcome (with a little help from Maple) is, again to my surprise: $$ \frac{1}{8}\left[ \,( h_1+h_2+h_3+h_4+h_5+h_6+h_7+h_8) \\ + (-h_1+h_2-h_3+h_4-h_5+h_6-h_7+h_8)\xi \\ + (-h_1-h_2+h_3+h_4-h_5-h_6+h_7+h_8)\eta \\ + (-h_1-h_2-h_3-h_4+h_5+h_6+h_7+h_8)\zeta \,\right] $$ The interpolation with the dual octahedron of an arbitrary hexahedron is linear again.
At last, according to
Wikipedia:
In all dimensions higher than four, there are only three convex regular
polytopes: the simplex, the hypercube, and the cross-polytope. In three
dimensions, these coincide with the tetrahedron, the cube, and the octahedron.
Where the (self-dual, linear) simplex may be considered as a trivial case.
Question. In all dimensions higher than three, does the isoparametric transformation give a linear interpolation for an arbitrary function discretized at the dual polytope of a "finite element" with the hypercube or the cross-polytope as a parent?