-1

I have been trying to make a single equation for more than one polygon by just changing the numbers that the variables represent and I can't figure out how to do so, so any help with that would be nice.

Ewan Cazar
  • 41
  • 6
    Can you show us what you mean by an equation for a polygon? Perhaps with a few examples. – Blitzer Dec 16 '21 at 16:24
  • Well I am looking for an equation that doesn't make just one polygon, rather multiple when a variable's input is changed, so an equation that has no one answer. – Ewan Cazar Dec 16 '21 at 17:12
  • 2
    @EwanCazar, what Blitzer is asking for is some clarity on what it means to associate a polygon with an equation. The only example that comes to (my) mind is $|x|+|y|=D$, the solution set to which is a square with sides of length $\sqrt2D$. Is this the sort of thing you have in mind? – Barry Cipra Dec 16 '21 at 17:30
  • I know what Blitzer was asking, I myself cannot give a reasonable response to the question but the example you gave is an example of a expression with only 1 outcome I am looking for an equation that can give more than one outcome. – Ewan Cazar Dec 16 '21 at 17:34
  • @EwanCazar, I just edited my comment to give a family of examples, indexed by the variable $D$. They are all squares, of course, in part because I can't think offhand of any simple equation for a triangle or other polygon. (One can also get families of rhombi from $|ax|+|by|=|c|$.) – Barry Cipra Dec 16 '21 at 17:35
  • 1
    Related: "Is there any equation for triangle?". Also "Is there a single equation describing a triangle ..." references a Stand-up Maths video on the topic. Triangles alone are complicated, so a formula for "all polygons" is quite an ask; perhaps restricting to, say, regular polygons centered at the origin would be a good start. ... In any case, please provide some context about your skill level, to help people avoid explaining things that you already understand or using techniques that you might not. – Blue Dec 16 '21 at 17:55
  • Ok this it helpful thanks. – Ewan Cazar Jan 04 '22 at 15:01
  • The solutions to $z^n=1$ form a regular polygon in the complex plane with n sides. – user317176 Jan 11 '22 at 00:06
  • @Blue I have completely changed my answer including now 1) it is valid for any type of regular polygon, 2) It is justified by Viviani theorem, 3) it has an interesting 3D interpretation. – Jean Marie Jan 12 '22 at 19:54

1 Answers1

2

There exists a general implicit equation, valid for any regular polygon (same sidelengths, same angles), centered in the origin with $n$ vertices:

$$f(x,y)=\sum_{k=1}^n \ \underbrace{|x \cos(r+ka)+y \sin(r+ka)-p|}_{d_k}=np \tag{1}$$

where

  • $a:=\frac{2\pi}{n}$

  • $r$ is an angular value giving the rotation angle of the figure around the origin.

  • $p$ gives the overall size of the polygon.

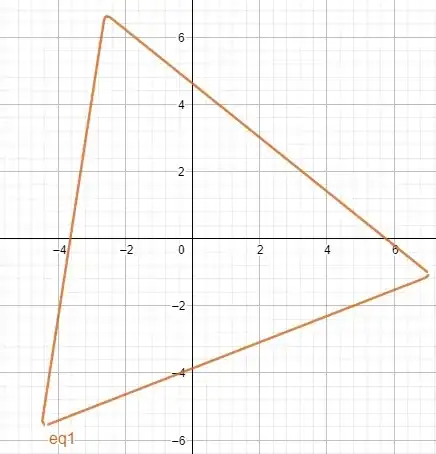
Here is a particular case with $n=3, p=3.5, r=-1.2$:

enter image description here

Proof: Expression (1) is due to a generalization of Viviani theorem expressing the fact that the sum of distances $d_k$ from any interior point of a regular polygon to its sides is a certain constant. See for example here.

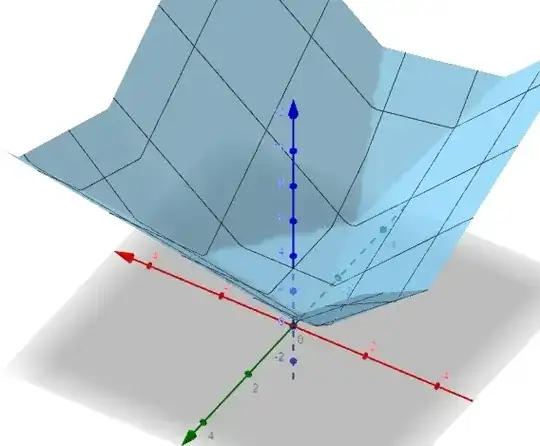
It is interesting to consider the surface with equation

$$z=f(x,y)=\sum_{k=1}^n \ |x \cos(r+ka)+y \sin(r+ka)-p|\tag{2}$$

Please note the difference between (1) and (2): the LHS is no longer restricted to value $np$.

The structure of this surface shows that $z=np$ is a limit case corresponding to a filled triangle, and as soon as we are on a "level set" $np+\varepsilon$, we have a triangle reduced to its sides ; a triangle ? Not really. A triangle with "chamfered" vertices... a phenomena that takes more and more importance as $z$ increases...

enter image description here

Remark; There are rather similar formulas for other types of shapes, for example this one gives a quarter plane that can take any position in the plane:

$$f(x,y)=|x \cos(a+c)+y \sin(a+c)|+x \cos(2a+c)+y \sin(2a+c)=b$$

See as well this reference.

Jean Marie
  • 81,803