Inside / Outside a Linear Tetrahedron
This answer is a straightforward generalization of the Inside / Outside problem
in de 2-D case, for a linear triangle. The clue is provided by a Finite Element approach.
Let's consider the simplest non-trivial finite element shape in 3-D, which is
a
linear tetrahedron.
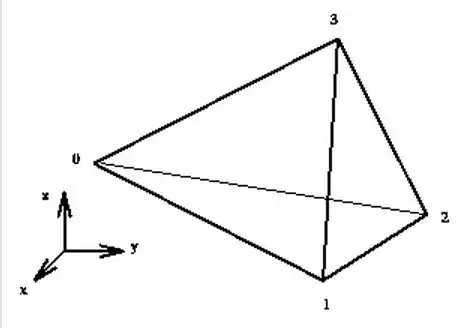
Function behaviour is approximated inside such a
tetrahedron by a
linear interpolation between the function values at the
vertices, also called nodal points. Let $\,T,$ be such a function, and
$\,x,y,z\,$ coordinates, then:
$$
T = A.x + B.y + C.z + D
$$
Where the constants A, B, C, D are yet to be determined.
Substitute $ x=x_k $ , $ y=y_k $ , $ z=z_k $ with $ k=0,1,2,3 $ .
Start with:
$$
T_0 = A.x_0 + B.y_0 + C.z_0 + D
$$
Clearly, the first of these equations can already be used to eliminate the
constant $D$, once and forever:
$$
T - T_0 = A.(x - x_0) + B.(y - y_0) + C.(z - z_0)
$$
Then the constants $A$ , $B$ , $C$ are determined by:
$$ \begin{array}{ll}
T_1 - T_0 = A.(x_1 - x_0) + B.(y_1 - y_0) + C.(z_1 - z_0) \\
T_2 - T_0 = A.(x_2 - x_0) + B.(y_2 - y_0) + C.(z_2 - z_0) \\
T_3 - T_0 = A.(x_3 - x_0) + B.(y_3 - y_0) + C.(z_3 - z_0)
\end{array} $$
Three equations with three unknowns. A solution can be found:
$$
\left[ \begin{array}{c} A \\ B \\ C \end{array} \right] =
\left[ \begin{array}{ccc} x_1-x_0 & y_1-y_0 & z_1-z_0 \\
x_2-x_0 & y_2-y_0 & z_2-z_0 \\
x_3-x_0 & y_3-y_0 & z_3-z_0 \end{array} \right]^{-1}
\left[ \begin{array}{c} T_1-T_0 \\ T_2-T_0 \\ T_3-T_0 \end{array} \right]
$$
It is concluded that $A,B,C$ and hence $(T-T_0)$ must be a linear expression
in the $(T_k-T_0)$:
$$
T - T_0 = \xi.(T_1 - T_0) + \eta.(T_2 - T_0) + \zeta.(T_3 - T_0)
$$ $$ =
\left[ \begin{array}{ccc} \xi & \eta & \zeta \end{array} \right]
\left[ \begin{array}{c} T_1-T_0 \\ T_2-T_0 \\ T_3-T_0 \end{array} \right]
$$
$$ =
\left[ \begin{array}{ccc} \xi & \eta & \zeta \end{array} \right]
\left[ \begin{array}{ccc} x_1-x_0 & y_1-y_0 & z_1-z_0 \\
x_2-x_0 & y_2-y_0 & z_2-z_0 \\
x_3-x_0 & y_3-y_0 & z_3-z_0 \end{array} \right]
\left[ \begin{array}{c} A \\ B \\ C \end{array} \right]
$$
$$ = T - T_0 =
\left[ \begin{array}{ccc} x-x_0 & y-y_0 & z-z_0 \end{array} \right]
\left[ \begin{array}{c} A \\ B \\ C \end{array} \right]
$$
Hence:
$$ \begin{array}{ll}
x - x_0 = \xi .(x_1 - x_0) + \eta.(x_2 - x_0) + \zeta.(x_3 - x_0) \\
y - y_0 = \xi .(y_1 - y_0) + \eta.(y_2 - y_0) + \zeta.(y_3 - y_0) \\
z - z_0 = \xi .(z_1 - z_0) + \eta.(z_2 - z_0) + \zeta.(z_3 - z_0)
\end{array} $$
But also:
$$
T - T_0 = \xi.(T_1 - T_0) + \eta.(T_2 - T_0) + \zeta.(T_3 - T_0)
$$
Therefore the
same expression holds for the function $\,T\,$ as well as for
the coordinates $\,x,y,z$ . This is called an
isoparametric transformation.
It is remarked without proof that the
local coordinates $\,\xi,\eta,\zeta\,$
within a tetrahedron can be interpreted as sub-volumes, spanned by the vectors
$\,\vec{r}_k-\vec{r}_0\,$ and $\,\vec{r}-\vec{r}_0\,$ where $\,\vec{r}=(x,y,z)\,$ and
$\,k=1,2,3$ .
Reconsider the expression:
$$
T - T_0 = \xi.(T_1 - T_0) + \eta.(T_2 - T_0) + \zeta.(T_3 - T_0)
$$
Partial differentiation to $ \xi $ , $ \eta $ , $ \zeta $ gives:
$$
\partial T / \partial \xi = T_1 - T_0 \quad ; \quad
\partial T / \partial \eta = T_2 - T_0 \quad ; \quad
\partial T / \partial \zeta = T_3 - T_0
$$
Therefore:
$$
T = T(0) + \xi \frac{\partial T}{\partial \xi}
+ \eta \frac{\partial T}{\partial \eta}
+ \zeta \frac{\partial T}{\partial \zeta}
$$
This is part of a Taylor series expansion around the node $(0)$. Such Taylor series
expansions are very common in Finite Difference analysis.
Now rewrite as follows:
$$
T = (1 - \xi - \eta - \zeta).T_0 + \xi.T_1 + \eta.T_2 + \zeta.T_3
$$
Here the functions $\,(1-\xi-\eta-\zeta)\,,\,\xi\,,\,\eta\,,\,\zeta\,$ are called the
shape functions of a Finite Element. Shape functions $\,N_k\,$ have the property
that they are unity in one of the nodes (k), and zero in all other nodes.
In our case:
$$
N_0 = 1-\xi-\eta-\zeta \quad ; \quad N_1 = \xi \quad ; \quad N_2 = \eta
\quad ; \quad N_3 = \zeta
$$
So we have two representations, which are allmost trivially equivalent:
$$ \begin{array}{ll}
T = T_0 + \xi.(T_1 - T_0) + \eta.(T_2 - T_0) + \zeta.(T_3 - T_0) \quad
& \mbox{: Finite Difference like} \\
T = (1 - \xi - \eta - \zeta).T_0 + \xi.T_1 + \eta.T_2 + \zeta.T_3 \quad
& \mbox{: Finite Element like}
\end{array} $$
Let's solve $\,\xi,\,\eta,\,\zeta$ from the equations, with
Cramer's rule :
$$ \begin{array}{ll}
x - x_0 = \xi .(x_1 - x_0) + \eta.(x_2 - x_0) + \zeta.(x_3 - x_0) \\
y - y_0 = \xi .(y_1 - y_0) + \eta.(y_2 - y_0) + \zeta.(y_3 - y_0) \\
z - z_0 = \xi .(z_1 - z_0) + \eta.(z_2 - z_0) + \zeta.(z_3 - z_0)
\end{array} $$
$$
\xi = \left| \begin{array}{ccc} x-x_0 & x_2-x_0 & x_3-x_0 \\
y-y_0 & y_2-y_0 & y_3-y_0 \\ z-z_0 & z_2-z_0 & z_3-z_0 \end{array} \right|
/ D \\
\eta = \left| \begin{array}{ccc} x_1-x_0 & x-x_0 & x_3-x_0 \\
y_1-y_0 & y-y_0 & y_3-y_0 \\ z_1-z_0 & z-z_0 & z_3-z_0 \end{array} \right|
/ D \\
\zeta = \left| \begin{array}{ccc} x_1-x_0 & x_2-x_0 & x-x_0 \\
y_1-y_0 & y_2-y_0 & y-y_0 \\ z_1-z_0 & z_2-z_0 & z-z_0 \end{array} \right|
/ D $$ Where: $$
D = \left| \begin{array}{ccc} x_1-x_0 & x_2-x_0 & x_3-x_0 \\
y_1-y_0 & y_2-y_0 & y_3-y_0 \\ z_1-z_0 & z_2-z_0 & z_3-z_0 \end{array} \right|
$$
The Inside / Outside function IO of the tetrahedron is defined as follows.
$$
\mbox{IO} =\mbox{min}(N_0,N_1,N_2,N_3) =
\mbox{min}(\xi,\,\eta,\,\zeta,\,1-\xi-\eta-\zeta)
$$ The maximum of the IO function is reached for
$\,\xi = \eta = \zeta = 1-\xi-\eta-\zeta = 1/4 $ ,
hence at the midpoint (barycenter) of the tetrahedron. If we draw straight
lines from the the midpoint towards the vertices, and further, then the whole
space is subdvided into four regions, one where IO $= \xi$ , one where IO $= \eta$ ,
one where IO $= \zeta$ , and one where IO $= 1-\xi-\eta-\zeta$ ; hope you get
the 4-D picture. The IO function is positive for points $(x,y,z)$ inside
the tetrahedron and negative for points $(x,y,z)$ outside the tetrahedron,
and zero for points at the boundaries. Moreover, the value of the function is sort
of a measure for the distance between $(x,y,z)$ and the barycenter.
I've taken notice of the fact that the OP has some programming experience.
So here comes a (Delphi Pascal) program snippet that is supposed
to do the mathematics:
program Stick;
type
matrix = array of array of double;
punt = record
x,y,z : double;
end;
punten = array of punt;
function det(mat : matrix) : double;
{
Determinant of 3 x 3 matrix
}
begin
det := mat[0,0]*mat[1,1]*mat[2,2]-mat[0,0]*mat[1,2]*mat[2,1]
-mat[1,0]*mat[0,1]*mat[2,2]+mat[1,0]*mat[0,2]*mat[2,1]
+mat[2,0]*mat[0,1]*mat[1,2]-mat[2,0]*mat[0,2]*mat[1,1] ;
end ;
function Identical(M : matrix) : matrix;
{
Make copy of matrix
}
var
i,j : integer;
S : matrix;
begin
SetLength(S,3,3);
for i := 0 to 2 do
for j := 0 to 2 do
S[i,j] := M[i,j];
Identical := S;
end;
procedure test;
var
T : array[0..3] of punt;
r : punt;
M,S : matrix;
i : integer;
D,xi,eta,zeta,IO : double;
begin
{ Vertices of Tetrahedron }
for i := 0 to 3 do
begin
T[i].x := Random;
T[i].y := Random;
T[i].z := Random;
end;
SetLength(M,3,3);
for i := 0 to 2 do
begin
M[0,i] := T[i+1].x-T[0].x;
M[1,i] := T[i+1].y-T[0].y;
M[2,i] := T[i+1].z-T[0].z;
end;
D := det(M);
SetLength(S,3,3);
{ Barycenter test }
r.x := (T[0].x+T1.x+T[2].x+T[3].x)/4;
r.y := (T[0].y+T1.y+T[2].y+T[3].y)/4;
r.z := (T[0].z+T1.z+T[2].z+T[3].z)/4;
{ Point in space }
r.x := Random;
r.y := Random;
r.z := Random;
S := Identical(M);
S[0,0] := r.x-T[0].x;
S[1,0] := r.y-T[0].y;
S[2,0] := r.z-T[0].z;
xi := det(S)/D;
S := Identical(M);
S[0,1] := r.x-T[0].x;
S[1,1] := r.y-T[0].y;
S[2,1] := r.z-T[0].z;
eta := det(S)/D;
S := Identical(M);
S[0,2] := r.x-T[0].x;
S[1,2] := r.y-T[0].y;
S[2,2] := r.z-T[0].z;
zeta := det(S)/D;
IO := 1-xi-eta-zeta;
if IO > xi then IO := xi;
if IO > eta then IO := eta;
if IO > zeta then IO := zeta;
Writeln(IO);
if IO > 0 then Readln; { Inside }
end;
begin
while true do
test;
end.
Output, paused at Inside hit:
-3.57217102952215E+0000
-3.29649515391294E-0001
-6.94579094637227E-0001
-6.02022821324288E-0001
-3.00028147738175E-0001
-4.38988084865881E-0001
-4.44247003351889E-0001
-1.10578952640585E+0001
-4.84149144259875E-0001
-8.38910075699883E-0001
-4.40603226584686E-0001
6.93752218750558E-0003
Note. This approach is essentially not much different from establishing
whether a point is inside / outside a sphere with equation $\,R^2-(x^2+y^2+z^2)=0$ .

In fact, if we let $\vec{PA}$ be the vector from $P$ to $A$ and $\vec{F}_a$ be the outward pointing normal on the face opposite to $A$ with magnitude $F_a$. One can show $$\vec{PA} \cdot \vec{F}_a + \vec{PB} \cdot \vec{F}_b + \vec{PC} \cdot \vec{F}_c + \vec{PD} \cdot \vec{F}_d = -9V$$ where $\cdot$ now stands for vector dot product.
– achille hui Jan 20 '15 at 07:57