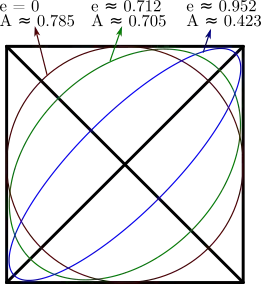
There is unique inscribed ellipse of a convex pentagon (dual case for $5$ points defining a conic). There are one and two degrees of freedom of drawing an inscribed ellipse in a (convex) quadrilateral and triangle respectively.
By means of skew transformation, we can transform an irregular quarilateral (convex but not parallelogram) into one with one pair of opposite sides are perpendicular.
$$(x',y')=(x+y\cos \omega,y\sin \omega)$$
Taking the vertices as $A(a,0)$, $B(b,0)$, $C(0,c)$ and $D(0,d)$ where $ab>0$, $cd>0$ and $(a-b)(d-c)>0$.
The two extreme cases are the ellipse degenerates into the diagonals.
Construct a family of conics touching with the axes with parameter $k$:
$$
\left[
k\left( \frac{x}{a}+\frac{y}{c} \right)+
(1-k)\left( \frac{x}{b}+\frac{y}{d} \right)-1
\right]^2=\lambda x y \tag{$\star$} $$
- Using a discriminant to check tangency for $\frac{x}{a}+\frac{y}{d}=1$ or $\frac{x}{b}+\frac{y}{c}=1$, we can solve for $\lambda$.
$$\lambda=4k(1-k)
\left(
\frac{1}{a}-\frac{1}{b}
\right)
\left(
\frac{1}{d}-\frac{1}{c}
\right)$$
$$4k(1-k)
\left(
\frac{1}{a}-\dfrac{1}{b}
\right)
\left(
\frac{1}{d}-\dfrac{1}{c}
\right)
\left(
\frac{k}{ac}+\frac{1-k}{bd}
\right)>0 \implies k\in (0,1) $$
- The centre of the ellipse lies on the Newton line which is the line joining the mid-points of the diagonals.
$$\text{centre}=\frac{
\left(
\dfrac{k}{c}+\dfrac{1-k}{d},\dfrac{k}{a}+\dfrac{1-k}{b}
\right)}{2
\left(
\dfrac{k}{ac}+\dfrac{1-k}{bd}
\right)}$$

Addendum
To generalize to any kind of convex quadrilateral, we may use the skew axes as the diagonals. Now taking the vertices as $A(a,0)$, $B(0,b)$, $C(c,0)$ and $D(0,d)$ where $ac<0$ and $bd<0$.
In tangential coordinates $(X,Y)$, tangent line $\frac{x}{a}+\frac{y}{b}=1$ can be written as $$Xx+Yy+1=0$$
Hence, the dual conic will pass through a "rectangle" with vectices $(-\frac{1}{a},-\frac{1}{b})$, $(-\frac{1}{c},-\frac{1}{b})$, $(-\frac{1}{c},-\frac{1}{d})$ and $(-\frac{1}{a},-\frac{1}{d})$, that is
$$\lambda (aX+1)(cX+1)+\mu (bY+1)(dY+1)=0$$
- Let $(\lambda,\mu) \propto (1-k,k)$, the inscribed ellipse is
$$\det
\begin{pmatrix}
0 & x & y & 1 \\
x & \lambda ac & 0 & \frac{\lambda (a+c)}{2} \\
y & 0 & \mu bd & \frac{\mu (b+d)}{2} \\
1 &\frac{\lambda (a+c)}{2} & \frac{\mu (b+d)}{2} & \lambda+\mu
\end{pmatrix}=0$$
The centre divides the Newton line, from $(0, \frac{b+d}{2})$ to $(\frac{a+c}{2},0)$ internally with ratio $\lambda:\mu$
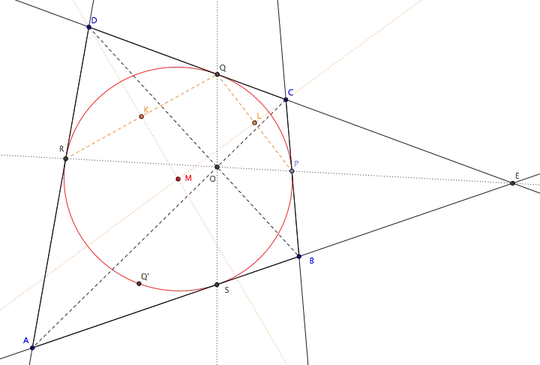
Illustration of dual conics pair: