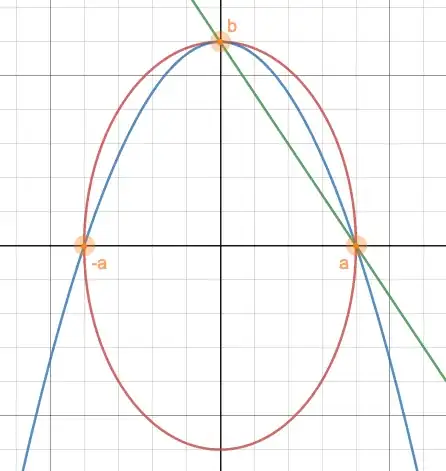
If you view the line as half of a degenerate "crossed-lines hyperbola" then the three curves can be parameterized by a variable second vertex.
Define
$$A = (2a,-b) \qquad B = (0,b) \qquad C = (-2a,-b) \qquad D = \left(-2a \delta, \frac{b}{\varepsilon}\right) \qquad E = \left(2a\delta, \frac{b}{\varepsilon}\right)$$
Note that I've moved things around a little, placing the origin halfway between the fixed vertex and the line containing the two other fixed points. (I've also made the distance between that point and line $2b$ instead of just $b$, and the distance between the two points on the line $4a$ instead of $2a$.) This is so that three special cases are easily described:
- $\varepsilon = \phantom{-}1$: Crossed lines through the upper fixed point.
- $\varepsilon = -1$: Parallel lines through the three fixed points.
- $\varepsilon = \phantom{-}0$. Parabola.
The specified ellipse corresponds to $\varepsilon = -1/3$.
These five points determine a conic with equation
$$\begin{align}
0 &= \left|\begin{array}{cccccc}
x^2 & y^2 & x y & x & y & 1 \\
A_x^2 & A_y^2 & A_x A_y & A_x & A_y & 1 \\
B_x^2 & B_y^2 & B_x B_y & B_x & B_y & 1 \\
C_x^2 & C_y^2 & C_x C_y & C_x & C_y & 1 \\
D_x^2 & D_y^2 & D_x D_y & D_x & D_y & 1 \\
E_x^2 & E_y^2 & E_x E_y & E_x & E_y & 1
\end{array}\right| \\[6pt]
&= \frac{32 a^2 b^2 \delta (1 + \varepsilon)}{\varepsilon^3}
\left(\;(1 - \varepsilon ) \left( - b^2 (1+\varepsilon) x^2 + 2 a^2 (y - b) (\varepsilon y - b)\right)
+ 4 a^2 \delta^2\varepsilon^2 \left( b^2 - y^2 \right)
\;\right)
\end{align}$$
Conveniently ignoring the possibility that $\delta$ could be zero (or that $\varepsilon$ could equal $0$ or $-1$), we remove the leading factor. But then we dutifully take $\delta$ to be $0$ anyway, so that points $D$ and $E$ coalesce at a vertex of the conic.
The resulting equation can be written
$$\frac{x^2}{a^2}\;\frac{1+\varepsilon}{2} \;=\; \frac{(y - b) (\varepsilon y - b)}{b^2}\tag{$\star$}$$
Let's review the special cases ...
- $\varepsilon = 1$: Crossed lines.
$$\frac{x^2}{a^2} = \frac{(y - b)^2}{b^2} \qquad\to\qquad y = \pm \frac{b}{a} x + b$$
- $\varepsilon = -1$: Parallel lines.
$$0 \;=\; (y - b) (y + b) \qquad\to\qquad y = \pm b$$
- $\varepsilon = 0$: Parabola.
$$\frac{x^2}{a^2} \;=\; - \frac{y - b}{b} \qquad\to\qquad y - b = -\frac{b}{a^2}x^2$$
- $\varepsilon = -1/3$. Ellipse centered the midpoint of $\overline{AC}$.
$$\frac{x^2}{a^2} \;=\; -\frac{(y - b) (y + 3 b)}{b^2} \qquad\to\qquad \frac{x^2}{(2a)^2} + \frac{(y+b)^2}{(2b)^2} = 1$$