How do I find an ellipse that is tangent to two non-orthogonal lines?

Question

I am trying to connect two lines (depicted below in red and blue) by an elliptical arc, such that the arc of ellipse runs seamlessly into those two lines.

1-3 below are the easy cases, but they should give a good idea of what I am trying to do. 1 and 3 are easy because they can be accomplished with an arc of a circle.

Case 2 is easy because a circle can be scaled along one axis to create the desired ellipse.

Case 4 is where I am stuck. Simply scaling a circular arc doesn't work. If I took the arc from case 3 and scaled it to fit the space, it would no longer be tangent with the top line.

Is there a mathematical way to solve this problem?

Is the solution significantly different when the depicted angle is acute vs. obtuse?

Answer 1

With

$$ \cases{ p = (x,y)\\ p_1=(x_1,y_1)\\ p_2=(x_2,y_2)\\ v_1 = (v_{x_1},v_{y_1})\\ u_1 = (-v_{y_1},v_{x_1})\\ v_2 = (v_{x_2},v_{y_2})\\ u_2 = (-v_{y_2},v_{x_2})\\ A = \left(\matrix{a& \frac b2\\ \frac b2& c}\right)\\ B = \left(\matrix{d & e}\right) } $$

and the ellipse $E(p) = p'Ap+Bp+f=0$ we have the conditions:

$$ \cases{ E(p_1)=0\\ E(p_2)=0\\ \nabla E(p_1) = \lambda_1 u_1\\ \nabla E(p_2) = \lambda_2 u_2\\ \det(A) \gt 0 } $$

so we have $7$ equations and $8$ unknowns $(a,b,c,d,e,f,\lambda_1,\lambda_2)$.

From $\nabla E(p_i) = 2p_i'A + B = \lambda_i u_i$ we can obtain $\lambda_i$ easily. After dot right multiplication by $p_i$ we obtain

$$ \lambda_i = \frac{2p_i'Ap_i+Bp_i}{u_ip_i} $$

thus we have

$$ \cases{ p_i'Ap_i+Bp_i + f = 0\\ \det(A) \gt 0\\ 2p_i'A + B = \left(\frac{2p_i'Ap_i+Bp_i}{u_ip_i}\right)u_i\\ }\ \ \ \ \ \ \ (*) $$

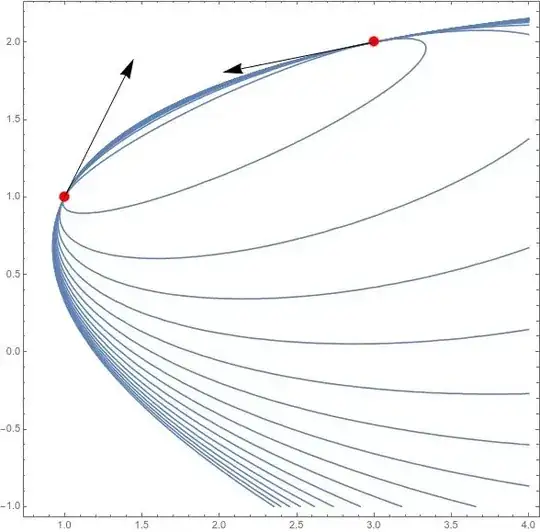
Focusing a case study having

$$ \cases{ p_1=(1,1)\\ p_2=(3,2)\\ v_1 = (\frac 12,1)\\ u_1 = (-1,\frac 12)\\ v_2 = (-1,-\frac 15)\\ u_2 = (\frac 15,-1)\\ \det(A) =a c-\frac{b^2}{4}=1 } $$

from $(*)$ we have the equations

$$ \left\{ \begin{array}{rcl} a+b+c+d+e+f & = & 0\\ 9 a+6 b+4 c+3 d+2 e+f & = & 0 \\ a c-\frac{b^2}{4}-1 & = & 0\\ -2 a-3 b-4 c-d-2 e & = & 0\\ 2 a+3 b+4 c+d+2 e & = & 0\\ \frac{2}{7} (30 a+13 b+4 c+5 d+e) & = & 0\\ -\frac{3}{7} (30 a+13 b+4 c+5 d+e) & = & 0\\ \end{array} \right. $$

Note that two equations can be eliminated so now we have $(5)$ equations and $(6)$ unknowns $(a,b,c,d,e,f)$ so we will solve for $(a,b,c,d,e)$ obtaining $(a(f),b(f),c(f),d(f),e(f)$ as follows

$$ \left[ \begin{array}{ccccc} a&b&c&d&e\\ \frac{1}{37} \left(19 f-6 \sqrt{9 f^2-37}\right) & \frac{2}{37} \left(13 \sqrt{9 f^2-37}-35 f\right) & \frac{2}{37} \left(41 f-11 \sqrt{9 f^2-37}\right) & \frac{2}{37} \left(10 f-9 \sqrt{9 f^2-37}\right) & \frac{4}{37} \left(5 \sqrt{9 f^2-37}-22 f\right) \\ \end{array} \right] $$

Here we can choose $f$ to define the best fit. Follows a plot shoving the solutions parameterized by $f$.

Answer 2

There are surely multiple ways to attack case 4. In fact, the solution will not be unique.

Five distinct points in general position in a plane determine a conic uniquely if the conic must pass through all five points. Four points is not enough. You can substitute a given tangent line for a given point, but you have only two points and two tangent lines, so there is still a remaining degree of freedom in your ellipse (or at least there will be in most cases where there is a solution).

A general equation for any conic section is $$Ax^2+By^2+Cxy+Dx+Ey+F=0. \tag1$$ The slope of the tangent at a point on this curve satisfies the equation $$ (2By+E+Cx)\frac{\mathrm dy}{\mathrm dx} + 2Ax+D+Cy = 0. \tag2 $$

So at each of your two points, plug the $x$ and $y$ coordinates into Equation $(1)$. That gives you two equations that are each linear in the six unknowns $A,B,C,D,E,F$. Again at each of the two points, plug the $x$ and $y$ coordinates and the slope $\frac{\mathrm dy}{\mathrm dx}$ of the tangent line into Equation $(2)$. That gives you two more linear equations in the same six unknowns.

With those four equations, you can reduce the problem to two parameters, for example $A$ and $B$, such that you have equations telling you what the value of each other unknown will be when these two unknowns are set. That looks like two degrees of freedom, but one of them is just due to the fact that you can always multiply the six coefficients of Equation $(1)$ without changing the conic that satisfies it. The second variable actually changes the shape of the conic. If an ellipse is possible (it isn't always), there will generally be some variability in its shape.

---

Note that the same solution method works for cases 1, 2, and 3 as well. The solutions in those cases also are not unique; there just happen to be particular solutions that are easy to see.

What is different between case 4 and the other cases is that in the first three cases, the easy solutions give you an ellipse with its center at the intersection of your two line segments. In case 4, there is no solution with the center of the ellipse at the intersection of the line segments, because in a non-circular ellipse, the only radial lines that intersect the ellipse at right angles are the major axis and the minor axis. So in case 4 the center has to be somewhere else.