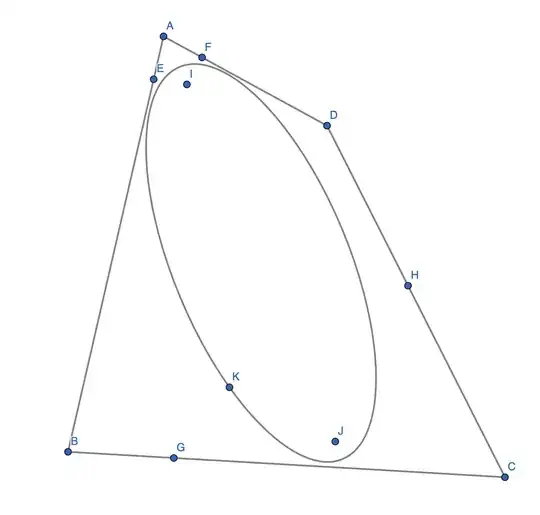
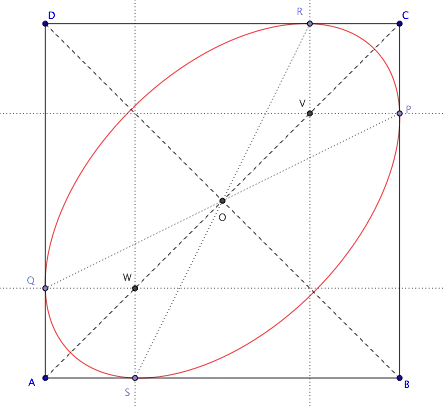
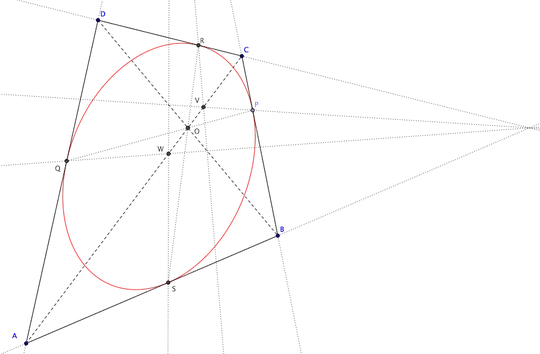
As mentioned in the comments, you can apply a projective transformation and turn the quadrilateral into a square. This works because if you hit an ellipse with a projective transformations that keeps it bounded it remains an ellipse. So we deal with that case from now on.
Let the four sides of $S$ be denoted $S_R, S_L,S_T, S_B$, with subscript standing for right, left, top, bottom. Let's assume that $S_B$ is the $x$-axis; this will be notationally convenient later.
The question is : given $p_i \in S_i$, $i \in \{R,L,T,S\}$, is there an inscribed ellipse tangent to the four sides at the $p_i$?
An algorithm to decide this equation (and produce the ellipse if it exists) is sketched below. The moral of the story is that it is a linear algebra problem.
An ellipse $E$ has a general formula: $$a x^2 + by^2 + c xy + dx + ey + f= 0.$$
If we assume $f \not = 0$, we can normalize it to $1$. (You can avoid this annoying case analysis with projective coordinates.) Let's assume we are in this case, and I'll leave the other case to you, so the equation is:
$$a x^2 + by^2 + c xy + dx + ey + 1= 0.$$
Note that there are 5 variables here, so we have a five dimensional vector space with coordinates $(a,b,c,d,e)$.
Consider the point $p_i = (x_i, y_i)$. If $p_i \in E$, then $a x_i^2 + by_i^2 + c x_iy_i + dx_i + ey_i + 1 = 0.$ The $x_i, y_i$ are fixed numbers, so this is a linear equation in the variables $(a,b,c,d,e)$.
We get four such equations. The set of solutions to them will be a line(see footnote (*) ), which you can compute with linear algebra.
We now examine the condition that $E$ is tangent to the base of the square, namely the $x$-axis. The $x$-axis is defined by the equation $y = 0$, so the equation defining $E$ becomes $q(x) = ax^2 + dx + 1 = 0$ when we restrict to the $x$-axis.
One way to proceed from here is to use the fact that this quadratic is tangent to the $x$-axis iff the quadratic $q$ has a double root, which happens iff the discriminant vanishes, i.e. $d^2 - 4a = 0$. However, this is wasteful, since we have additional information; in particular, we know that $q(x)$ must touch tangentially at the particular point $p_B$. In particular, we want the derivative of $q$ to vanish at $x_B$.
So, we get one more condition, namely $q'(x) = 2a x + b$ vanishes at $x_B$, or $2ax_B + b = 0$.
This gives us five equations in general, cutting us down to a single conic, which might be your desired ellipse. To see whether corresponds to your ellipse, you can:
- Test if it is an ellipse by (symbolically) completing the square.
- Test each one against the 3 other tangency conditions.
- You can also make sure that it is on the right side of all 4 lines by checking the ellipse restricted to each of the four sides gives a quadratic with the correct sign in front of the quadratic term.
If the conic passes these tests, it is a solution to your problem. Otherwise, there is no solution with specification the given $p_i$.
I think these tests are likely to be redundant. In particular, I think an ellipse tangent to the four intervals must lie inside it, so you can probably eliminate the third condition.
(*) You can prove, I think, that the conditions do not conspire and become linearly dependent for bad choices of points. Fix your $p_i$. Then there is conic passing through $p_L$ but not $p_B$. Also, there is a conic passing through $p_L$ and $p_B$, but not $p_R$. Finally, there is a conic passing through $p_L, p_B, p_R$ but not $p_U$. I didn't formally verify these statements, just did some doodles with parabolas and circles, so I'd double check this point. I think the same is true regarding imposing the final linear condition that one of these intersections is tangential.
If this is correct, then each time you add one of these conditions you necessarily eliminate some conics, meaning that the dimension of the space drops when you impose the new constraint.
A more algebraic and believable argument would be to explicitly construct equations a sequence of conics achieving each of these intermediate conditions.
Remark I believe the following is true: For each $x \in S_B$ there is a unique ellipse tangentially inscribed in $S$ that contains $x$, provided $x$ is not at a corner. So, there is actually an interval of ellipses satisfying you constraints. I'm not sure about this though. I think that via projective duality the above argument would give uniqueness. I convinced myself of existence through a half backed argument about inflating an ellipse passing through $x$ and the antipode of $x$ around the midpoint of the square, but I'm not sure if it can be easily formalized.