This question might seem vague, but what does a one parameter family of conics mean? Is it similar to how we define a one-parameter family of curves?
-
It is indeed an instance of a one-parameter family of curves, as a conic is a curve. – Dec 23 '19 at 19:22
1 Answers
Different parameters serve different purposes. We can observe how the mathematical nature evolves by varying one particular parameter. See below, several examples with the varying parameters in $\color{red}{red}$:
Conics with fixed semi-latus rectum and focus:
$$r=\frac{\ell}{1+\color{red}{e}\cos \theta}$$
Conics with fixed periapsis and focus:
$$r=\frac{r_p(1+\color{red}{e})}{1+\color{red}{e}\cos \theta}$$
Family of conics touching the axes at $(a,0)$ and $(0,b)$:
$$ \left( \frac{x}{a}+\frac{y}{b}-1 \right)^2 =\frac{2\color{red}{\lambda} xy}{ab} \tag{$\lambda \ne 0$}$$
Confocal central conics:
$$\frac{x^2}{a^2+\color{red}{s}}+\frac{y^2}{b^2+\color{red}{s}}=1$$
Confocal parabolae:
$$y^2=2\color{red}{\lambda} x+\color{red}{\lambda}^2$$
Lissajous figures of two signals with the same frequencies:
$$\frac{x^2}{a^2}-\frac{2xy\cos \color{red}{\phi}}{ab}+\frac{y^2}{b^2} =\sin^2 \color{red}{\phi}$$
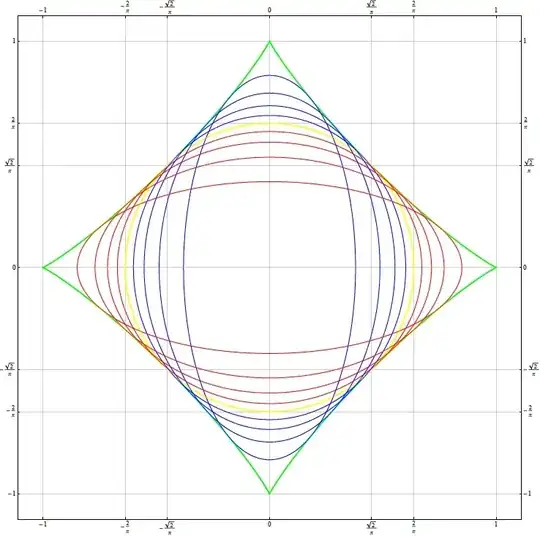
Isoperimetric ellipses (see more on the link here):
$$x^2+\frac{y^2}{1-\color{red}{k}^2}= \left[ \frac{p}{4E(\color{red}{k})} \right]^2$$
$$\frac{x^2}{1-\color{red}{k}^2}+y^2= \left[ \frac{p}{4E(\color{red}{k})} \right]^2$$
- 18,990