\begin{align*}
p &= 4a E(k) \\
a(k) &= \frac{p}{4E(k)} \\
F(x,y,k) &=
x^2+\frac{y^2}{1-k^2}-\frac{p^2}{16E^2(k)} \\
\frac{\partial F}{\partial k} &=
\frac{2ky^2}{(1-k^2)^2}-
\frac{p^2}{8E^3(k)} \left[ \frac{K(k)-E(k)}{k} \right]
\end{align*}
The envelope is given by $$F=\dfrac{\partial F}{\partial k}=0$$
On solving,
$$
\begin{pmatrix}
x \\ y
\end{pmatrix}=
\frac{p}{4kE(k)}
\begin{pmatrix}
\pm \sqrt{1-\dfrac{(1-k^2)K(k)}{E(k)}} \; \\[5pt]
\pm (1-k^2)\sqrt{\dfrac{K(k)}{E(k)}-1} \;
\end{pmatrix} \, , \quad 0<k<1 \tag{1}
$$
If we adimit $a<b$, then
$$
\begin{pmatrix}
x \\ y
\end{pmatrix}=
\frac{p}{4kE(k)}
\begin{pmatrix}
\pm (1-k^2)\sqrt{\dfrac{K(k)}{E(k)}-1} \; \\[5pt]
\pm \sqrt{1-\dfrac{(1-k^2)K(k)}{E(k)}} \;
\end{pmatrix} \, , \quad 0<k<1 \tag{2}
$$
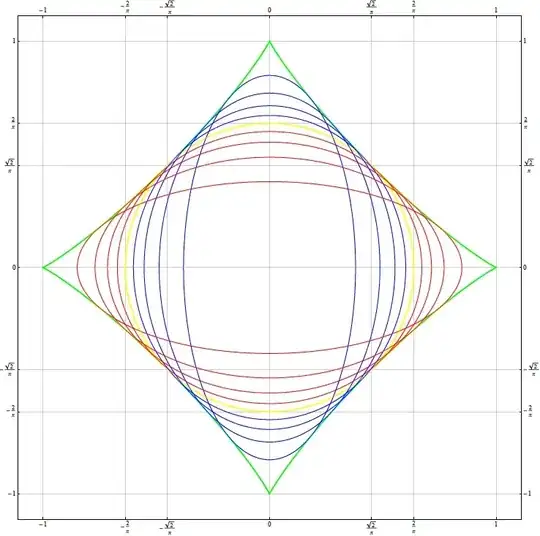
A plot of the envelope for $p=4$ with the ellipses is shown below: