The infamous "$\pi = 4$" proof was already discussed here:
And I have read all the answers, yet I think that they will not be of much help to me if I try to explain this thing to a non mathematician. The main missing point, in my opinion, is the fact that length of curves is defined using polygonal approximations (discrete approximation of the curve obtained by taking the straight-lines connecting a finite sequence of points on the curve).
However, a layman would ask "why is your strange 'polygonal approximation' method correct, but the $\pi = 4$ proof's method incorrect?" and I have to admit I fail to see strong arguments to convince him here.
So my question might be better stated as "convince a layman the correct way to measure lengths of curves is our (the mathematician's) way"; however, I'm interested specifically in the $\pi = 4$ proof and will be glad to hear totally different approaches to it.
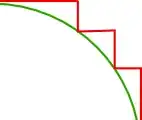

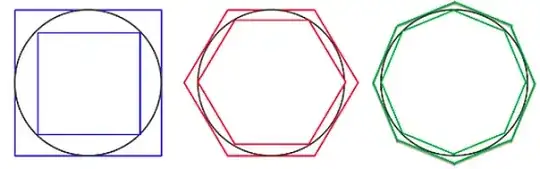

The π=4 method isn't "incorrect", it just gives a different notion of distance than Euclidean distance. In fact, the distance it gives is perfectly valid: it's the taxicab metric perimeter of the circle. It's a perfectly reasonable notion of distance, it just isn't the Euclidean distance we talk about in every day life: the one that is invariant under rigid rotations/translations, etc.
– Marcel Besixdouze Mar 15 '16 at 21:55