Why is the "staircase proof" that $\pi=4$ incorrect?

Question

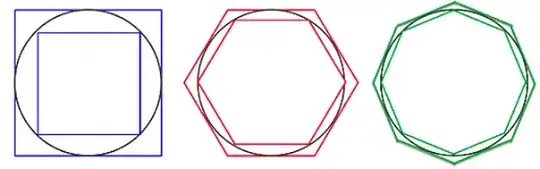
Given a few similar questions, I pretty much know why the following argument is incorrect:

But consider a similar situation in which the sides of a regular polygon are tangent to a circle (actually, as above, the circle is inside the polygon). We know that as the number of sides of the polygon increases, the area of the polygon approaches the area of the circle.

But it can also be seen intuitively that as the number of sides of the polygon increases, the perimeter of the polygon approaches the perimeter of the circle. This intuition is correct here, but why was it incorrect in the above argument?!

Answer 1

The mathematical substance of your question has been addressed in many places. Here is one: The staircase paradox, or why $\pi\ne4$

You are asking a philosophical or psychological question about intuition. The short answer is that it's just intuition and needs to be trained. A good outfielder has good intuition about where to run to catch a fly. A good programmer has good intuition about what kind of algorithm will solve a particular problem. A good cook has good intuition about combining spices. In all these cases and in mathematics, you develop intuition with practice.

Newton had good intuition about how to reason with infinitesimal quantities long before mathematicians could formalize what we now study as limits. The more analysis you learn the better your intuition will help you see what works and what doesn't.

In your particular example the correct intuition is that to approximate the length of a curve you should use short segments that roughly parallel the curve. The perimeters of those boxes don't, even when the boxes are very small. The boxes are appropriate when you want to approximate an area with a curved boundary.