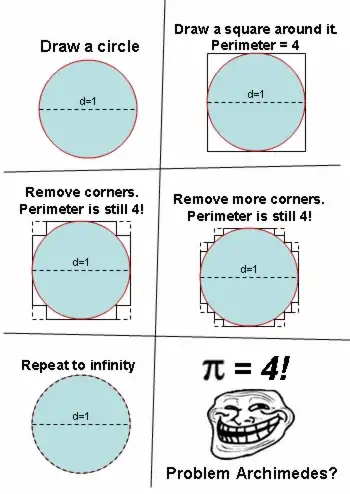
This is an interesting question. I think the key to it is to delve into the proof that two expressions for the length of a smoothly parameterized curve $\gamma : [a,b] \to \mathbb{R}^n$ give the same answer. The key thing to exploit is that the vector valued derivative $\gamma'(t)$ is uniformly continuous, which obviously fails for the Manhattan metric approximating curve.
The first expression for length is the one from calculus:
- $\text{Length}(\gamma) = \int_a^b \bigl| \gamma'(t) \bigr| \, dt$
and the other from metric space theory:
- $\text{Length}(\gamma)$ equals the supremum, over all partitions $a=t_0 < t_1 < ... < t_N = b$, of the length of the secant segment approximation $\sum_{n=1}^N \bigl|\gamma(t_n)-\gamma(t_{n-1})\bigr|$
Let me try to isolate the key issue of the proof of equality of 1 and 2 with a simple problem.
Suppose that I have a continuously differentiable function $f : [a,b] \to \mathbb{R}$ such that $f(a)=f(b)$, and hence the slope of the secant line between $(a,f(a))$ and $(b,f(b))$ equals zero. Suppose also that we have an upper bound $|f'(x)| \le B$ for all $x \in [a,b]$, and we imagine that $B$ is very close to zero. Consider the calculus expression the length of the graph $\Gamma = \{(x,f(x) \,|\, x \in [a,b]\}$
$$\text{Length}(\Gamma) = \int_a^b \sqrt{1 + f'(x)^2} \, dx \,
$$
What can be said about the value of this expression?
Well, we have an estimate for the integrand of the form
$$1 \le \sqrt{1 + f'(x)^2} \le \sqrt{1+B^2}
$$
which leads to a length estimate
$$\text{Length}[a,b] \le \text{Length}(\Gamma) \le \sqrt{1+B^2} \, \text{Length}[a,b]
$$
which leads to a length ratio estimate
$$1 \le \frac{\text{Length}(\Gamma)}{\text{Length}[a,b]} \le \sqrt{1+B^2}
$$
So as the bound $B$ gets closer and closer to zero, the length ratio gets closer and closer to $1$.
One can generalize this to the case that $f(a) \ne f(b)$, where the nature of the slope bound should be expressed in terms of the angle of the tangent line at each point compared to the angle of the secant line between $(a,f(a))$ and $(b,f(b)$, rather than in terms of slopes. One again obtains a uniformly bounded ratio of lengths, expressed in terms of a bound in the differences between angles.
Getting back to why 1 and 2 give the same result, the point is that if one chooses the partition $a=t_0<t_1<...<t_N=b$ to be very fine, uniform continuity of $\gamma'(t)$ guarantees that on the very short subinterval $[t_{n-1},t_n]$ the angle of $\gamma'(t)$ is very close to the angle of the secant segment approximation that connects the two points $\gamma(t_{n-1})$ and $\gamma(t_n)$ (where "very close" means that the bound is uniform over the segments). Therefore the integral expression for $n^{\text{th}}$ arc of $\gamma$, namely $\text{Length}(\gamma[t_{n-1},t_n])$, and the $n^{\text{th}}$ secant segment length, namely $\bigl| \gamma(t_n)-\gamma(t_{n-1})\bigr|$, have a ratio that is very close to $1$. Taking the sum from $n=1$ to $N$ we see that $1$ and $2$ have ratio that is very close to $1$. The ratio gets close and closer as the partition gets finer and finer, and hence 1 and 2 give the same answer.