Area under $x^{-x}$ over its real domain. What is another non-integral form of $\int_{\Bbb R^+}x^{-x}dx$?

Question

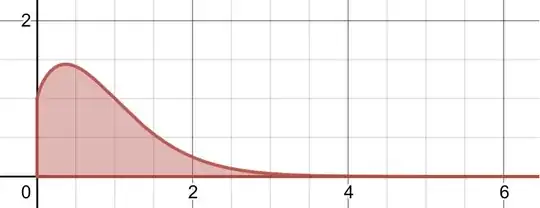
A few years ago, I got interested in an apparently hard integration problem which had me fascinated. This was the integral of a Sophomore Dream like integral except with the bounds over the real positive numbers denoted by $\Bbb R^+$ and not from 0 to 1 over the unit square, or unit line in this case? Nevertheless, this quirky problem caught my attention for having its area be almost 2 with this graph. Here is my solution, although there are a couple of calculations that I could have done differently: $$ A\mathit =\mathrm{\int_{\Bbb R^+}x^{-x}dx=\int_0^{\infty}\sum_{n=0}^{\infty}\frac{(-1)^nx^n ln^n(x)}{n!}dx}$$

I naively used Wolfram Alpha to integrate, but this can easily be still done with the substitution of $x=e^{-y}$ which is similar to the other Sophomore Dream integrals, so it will be ignored here for conciseness and should be able to use an interchanging theorem. Here I chose not to do the substitution as the same result appears anyways and this is simpler:

$$\mathrm{\sum_{n=0}^{\infty} \frac{(-1)^n}{n!}\int_0^{\infty}x^n ln^n(x)dx= \sum_{n=0}^{\infty} \frac{(-1)^n}{n!}(-x^{-n}x^nln^n(x)ln(x)ln^{-(n+1)}(x)(-1)^{-(n+1)}(n+1)^{-(n+1)}Γ\big(n+1,-(n+1)ln(x)\big)\big|_0^{\infty}= \sum_{n=0}^{\infty}\frac{Γ\big(n+1,-(n+1)ln(\infty)\big)}{Γ(n+1)(n+1)^{n+1}}}$$

This -$\infty$ in the gamma function argument does not seem to exist, but taking a limit helps as well as some other forms with the Regularized Incomplete Gamma Function: $$A=\mathrm{\sum_{n=1}^{\infty}n^{-n}\frac{Γ(n,-\infty n)}{Γ(n)}=\lim_{x\to \infty}\sum_{n\ge1}\frac{Q(n,-nx)}{n^n}=1.99545595…}$$

As seen from the link, the index n has to be a natural number which is true here. Also, there are other forms with the exponential sum function, and other series representations if non-elementary functions are not allowed. Here is proof of this answer from Wolfram Alpha.

Please do not give me any integral expressions of this constant, but rather special functions or other representations are encouraged. I will “check” the best answer. I just need a “nice” non-integral expression of the constant. Please give me feedback and correct me!

An alternate form solution is very needed for this problem also concerning power tower, so please check it out. I have left my context, attempts, and questions, therefore any help with alternate forms for either of these would be appreciated.

Using the definition of the Riemann Sum, we can rewrite this as:

$$\mathrm{\int_{\Bbb R^+}x^{-x}dx=\lim_{b,n\to \infty}\frac bn \sum_{k=0}^n\left(\frac{bk}{n}\right)^{-\left(\frac{bk}{n}\right)},n\gg b}$$

Here is proof of this result: Graph

Here are some unlikely closed forms.

There is also a form of the constant using a summation expansion. Here is proof of a third form of this constant here: $$\mathrm{A= \lim_{x\to \infty}\sum_{n\ge 1}\sum_{k=0}^{n-1}\frac{(-1)^k e^{nx} n^{k-n}x^k}{k!}}$$

Here is another sum and double sum answer here. This has a sophomore dream in the solution plus the same integrand from 1 to $\infty$: $$\mathrm{A=\sum_{n\ge 1}n^{-n}-\lim_{x\to \infty}\sum_{n\ge1}\sum_{k\ge1}\frac{(-x)^n(nx)^k}{(k+n)k!n!}}$$

Let $\bar F$ represent a Regularized Hypergeometric function then, as $\mathrm{Q(n,-nx)= 1-(-nx)^n\ _1\bar F_1(n,n+1,nx)}$, the following can be proven with the Kummer Confluent Hypergeometric Function: $$\mathrm{\sum_{n\ge1}n^{-n}-\lim_{x\to\infty}\sum_{n\ge1}(-x)^n\ _1\bar F_1(n,n+1,nx)}$$

Also, feel free to use these identities to find an alternate form. I could go on, but I have found no form that does not need a limit in the answer.

Answer 1

From : https://fr.scribd.com/doc/34977341/Sophomore-s-Dream-Function $$\text{Closed form : }\quad\int_0^\infty x^{-x}dx=\text{Sphd}(-1;\infty)$$ $$\text{Numerical value : Eq.(8:3).}$$

Before downvoting, please read "A schoolboy joke" pp.2-3 in the above referenced paper.

Answer 2

This is a note. I will try to find more in the near future. $$ I=\int^{\infty}_{0}x^{-x}dx=\int^{\infty}_{1}e^{-x\log x}dx+\int^{1}_{0}x^{-x}dx. $$ Using $\sum_{n\geq 1}n^{-n}=\int^{1}_{0}x^{-x}dx$ and making the change of variable $x\rightarrow e^{W(x)}$ where $W(x)$ is the well known Lambert function, we get $$ I=\sum_{n\geq 1}n^{-n}+\int^{\infty}_{0}\exp\left(-e^{W(x)}W(x)\right)e^{W(x)}W'(x)dx= $$ $$ =\sum_{n\geq 1}n^{-n}+\int^{\infty}_{0}e^{-x}e^{W(x)}W'(x)dx=\sum_{n\geq 1}n^{-n}+\int^{\infty}_{0}e^{-x}d\left(e^{W(x)}\right)= $$ $$ \textrm{ integration by parts } $$ $$ =\sum_{n\geq 1}n^{-n}-1+\int^{\infty}_{0}e^{-x}e^{W(x)}dx=\sum_{n\geq 1}n^{-n}-1+\int^{\infty}_{0}e^{-x}\frac{x}{W(x)}dx $$ If we make the change of variable $x\rightarrow -\log t$ we arrive easily to $$ I=\sum_{n\geq 1}n^{-n}-1+\int^{1}_{0}t\frac{-\log t}{W(-\log t)}\frac{-dt}{t}=\sum_{n\geq 1}n^{-n}-1+\int^{1}_{0}\frac{-\log t}{W(-\log t)}dt. $$ But the function $h(z)=\frac{W(-\log z)}{-\log z}$, is the analytic continuation of the Euler's iterated exponential function $z^{z^{z^{\ldots}}}$. Hence finaly we can write $$ \int^{\infty}_{0}\frac{1}{x^x}dx=\sum_{n\geq 1}\frac{1}{n^n}-1+\int^{1}_{0}\frac{1}{t^{t^{t^{ \ldots}}}}dt. $$ In the sense $z^{z^{z^{\ldots}}}=h(z)$.

REVISED.

Assume that $W(t)$ is the well known Lambert function. Then for $k=0,1,2,\ldots$, we have $$ \int^{M}_{0}\frac{t^k}{1+W(t)}dt=\frac{(-1)^{k+1}k!}{(k+1)^{k+1}}+ $$ $$ +\frac{M^{k+1} k!}{W(M)^{k+1}(k+1)^{k+1}}\sum_{0\leq j\leq k}(-1)^{j+k}\frac{(k+1)^jW(M)^j}{j!}. $$ Hence $$ \int^{M}_{0}\frac{e^{-t}}{1+W(t)}dt=-\sum^{\infty}_{k=0}\frac{1}{(k+1)^{k+1}}+ $$ $$ +\sum^{\infty}_{k=0}\frac{e^{-(k+1)W(M)} M^{k+1}W(M)^{-k-1}\Gamma(k+1,-(k+1)W(M))}{(k+1)^{k}(k+1)!}= $$ $$ =-\sum_{k\geq 1}k^{-k}+\sum_{k\geq 1}\frac{\Gamma(k,-kW(M))}{k^{k-1}k!},\tag 1 $$ where $$ \Gamma(a,z)=\int^{\infty}_{z}e^{-t}t^{a-1}dt $$ is the incomplete Gamma function. But one can see with the help of (1) easily that $$ \int^{M}_{1}x^{-x}dx=\int^{M\log M}_{0}\frac{e^{-t}}{1+W(t)}dt=-\sum^{\infty}_{k=1}k^{-k}+\sum^{\infty}_{k=1}\frac{\Gamma(k,-kW(M\log M))}{(k!) k^{k-1}}. $$ Hence using $\int^{1}_{0}x^{-x}dx=\sum^{\infty}_{k=1}k^{-k}$, we get $$ \int^{M}_{0}x^{-x}dx=\sum^{\infty}_{k=1}\frac{\Gamma(k,-k\log M)}{(k!) k^{k-1}}\textrm{, }\forall M>0.\tag 2 $$