Here is a possible answer for the integral of the gamma function. This then can be used to find “Γ” constant:
From source 1 with the nth derivative and source 2. Lets assume that the n=0 terms are by convention or limit defined. Here is a demo of the first series here:
1.$$\mathrm{Γ(x)=\sum_{n=0}^\infty \frac{Γ^{(n)}(1)x^{n-1}}{n!},|x|<1}$$
2.$$\mathrm{Γ^{(n)}(x)=\lim_{t\to 0} t^{-n}\sum_{m=0}^n(-1)^{n- m}\binom nm Γ(x+kt),n\in \Bbb N}$$
3.$$\mathrm {\int Γ(x)dx=\int \sum_{n=0}^\infty \frac{{\lim_{t\to 0} t^{-n}\sum_{k=0}^n(-1)^{n-k}\binom nk Γ(1+kt)}x^{n-1}}{n!}dx= \quad \lim_{t\to 0}\sum_{n=0}^\infty \sum_{k=0}^n \binom nk \frac{{
(-1)^{n-k}Γ(1+kt)}x^n}{t^nnn!}= \sum_{n=0}^\infty \frac{Γ^{(n)}(1)x^n}{nn!},|x|<1}$$
Also, you can use the fact that $$\mathrm{Γ(x+y)=Γ(y)\sum_{n=0}^\infty \frac {Γ^{(n)}(y)x^n}{Γ(y)n!},y\not \in \Bbb Z\ and \ y\not \le 0}$$
Therefore:
$$\mathrm{\int Γ(x+y) dx=\int Γ(y)\sum_{n=0}^\infty \frac {Γ^{(n)}(y)x^n}{Γ(y)n!} dx= \sum_{n=0}^\infty \frac {Γ^{(n)}(y)x^{n+1}}{(n+1)!}= \quad \lim_{t\to 0} \sum_{n=0}^\infty \sum_{k=0}^n \binom nk\frac {(-1)^{n-k}Γ(y+kt)x^{n+1}}{t^n(n+1)!}, y\not \in \Bbb Z \ and \ y\not \le 0}$$
You can also use the classic Riemann Sum Definition:
$$\int_a^b f(x) dx=\lim_{n\to \infty} \sum_{k=1}^n f(x_k=a+kΔx)Δx, Δx=\frac {b-a}{n}$$
to find that:
$$\mathrm{\int_a^b Γ(x) dx=\lim_{n\to \infty} \frac{b-a}{n} \sum_{k=1}^n Γ\left(a+k\frac{b-a}{n}\right)}$$
There also exists this expansion for the reciprocal gamma function which can be used to find the Fransén Robinson Constant, aka F, as there does not appear to be a restriction on the series. I will take Wolfram’s Website’s word that it converges. $\mathrm x_0$ is any real value to produce a vertical shift.
$$\mathrm{F=\int_{\Bbb R^+}\frac {dx}{Γ(x)}= \frac1\pi \sum_{k=0}^\infty \left(\sum_{n=0}^k \frac{\pi^{k-n}(-1)^nΓ^{(n)}(1-x_0)}{n!(k-n)!} sin\left(\pi x_0+\frac{\pi(k-n)}{2}\right)\right)\frac{(x-x_0)^{k+1}}{k+1} \mathop=^?\frac1\pi \sum_{k=0}^\infty \left(\sum_{n=0}^k \frac{\pi^{k-n}(-1)^n \lim_{t\to 0} t^{-n}\sum_{m=0}^n(-1)^{n- m}\binom nm Γ(1-x_0+kt)}{n!(k-n)!} sin\left(\pi x_0+\frac{\pi(k-n)}{2}\right)\right)\frac{(x-x_0)^{k+1}}{k+1}}$$
Here is another Beta Function based answer with the Pochhammer Symbol. Here is proof this really works
$$\mathrm{\int\frac{Γ(x)}{Γ(x+y)}dx=\frac1{Γ(y)}\left(ln(x)+\sum_{n=1}^\infty \frac{(1-y)_n}{n!}ln\left(1+\frac{x}{n}\right)\right)= \frac{lnx}{Γ(y)}+\sum_{n=1}^\infty\frac{sin(\pi y)(n-y)!}{\pi n!}ln\left(1+\frac{x}{n}\right),Re(y)>0}$$
Browsing Wolfram Mathworld made me find some generalized reciprocal factorial integral and generalized factorial integral functions. These are nicely named the Lamda function, Mu functions, and Nu functions. These may seem like they have the sole purpose of finding a closed form of an integral, but they should have some nice properties. Note I only list out a few:
$$\mathrm{λ(x,y)\mathop=^{def}\int_0^y \frac{t!}{x^t}dt, \frac{μ(x,y,z)\,y!}{x^z} \mathop=^{def}\int_0^\infty\frac{x^t t^y}{(t+z)!}dt,\frac{ν(x,z)}{x^z}=\int_0^\infty\frac{x^t}{(t+z)!}dt= \frac{μ(x,0,z)}{x^z},μ(x,y,0) \mathop=^{def}μ(x,y) ,ν(x,0) \mathop=^{def}ν(x)=μ(x,0,0)=μ(x,0)}$$
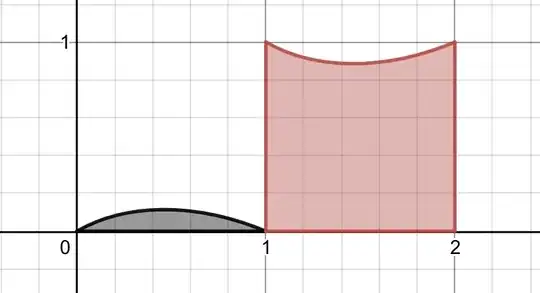
This means we can put our original problem and the Fransén-Robinson constant in closed form. Note the conventions for Γ in the question:
$$\mathrm{Γ \mathop=^{def}\int_{min\ Γ(x), x>0}^1 Γ^{-1}(x)dx=1-\int_0^1 t! dt=1-λ(1,1)= 0.0772540493193693948561195176…}$$
$$\mathrm{F \mathop=^{def} \int_{\Bbb R^+} \frac{dx}{Γ(x)}=\int_0^\infty \frac{1^t t^0dt}{Γ(t-1+1)}=μ(1,0,-1) =ν(1,-1)= 2.8077702420285193652215011865577…}$$
Please correct me and give me feedback!