Approximation of $\Big[\Gamma(1+x)\Big]^{-1}$ for $0 \leq x \leq 1$ (for the art for art's sake).

Question

Recently was asked on the site the question : how to compute $$f(t)=\int_0^t\frac{\mu^x}{\Gamma(x+1)}\ dx$$ for which I assumed $0 \leq t \leq 1$. There is no antiderivative available from any CAS I tried.

My first idea was to approximate $\Gamma(x+1)$ by a more or less constrained polynomial in $x$, then to use partial fraction decomposition. This leads to a linear combination of elliptic integrals.

Later, I found that $\Big[\Gamma(1+x)\Big]^{-1}$ looks to be very similar to a Gibbs excess energy diagram for a binary system. Some models of this physical properties are very simple (Van Laar, Margules), but they only have two parameters which is not enough for an "accurate" representation of the function. Much more accurate are Scatchard-Hildebrand, Wilson, NRTL or Uniquac models but their complexity would not allow the required integration.

So, with a limited choice, I decided to try with a model looking like the one proposed by Redlich-Kister which contains a pure polynomial component. So my idea was to write $$\frac{1}{\Gamma(x+1)}\sim 1+x(x-1) \sum_{k=0}^p d_k\, x^k$$ $$f(t)=\frac{\mu ^t-1}{L}+$$ $$\sum_{k=0}^p (-1)^k\,d_k L^{-(k+3)} (L\, \Gamma (k+2,-L t)+\Gamma (k+3,-L t)-(k+L+2) \Gamma (k+2))$$ where $L=\log(\mu)$ (provided that $\Re(\log (\mu ))<0\land \Re(k)>-2$).

Willing to stay non-empirical, in my answer, I used $p=3$ and the $d_k$'s were computed in order to match the function and first derivative values at $x=0$, $x=\frac 12$ and $x=1$. The result were no too bad.

For the art for art's sake, I decided to use $p=6$, the $d_k$'s were computed in order to match the function, first and second derivative values at $x=0$, $x=\frac 12$ and $x=1$. This leads to $$d_0=-\gamma \qquad d_1=-\gamma -\frac{\gamma ^2}{2}+\frac{\pi ^2}{12}$$

$$4 \sqrt \pi\,d_2=6 (178+3 \gamma (8+\gamma )) \sqrt{\pi }+32 \pi ^2-3 \pi ^{5/2}-64 \left(P^2+4 P+36\right)$$ $$3 \sqrt \pi\,d_3=-3 (1356+\gamma (111+16 \gamma )) \sqrt{\pi }-144 \pi ^2+8 \pi ^{5/2}+96 \left(3 P^2+8 P+92\right)$$ $$3 \sqrt \pi\,d_4=2 \left(3 (1376+\gamma (61+14 \gamma )) \sqrt{\pi }+156 \pi ^2-7 \pi ^{5/2}-24 \left(13 P^2+20 P+372\right)\right)$$ $$\frac{\sqrt{\pi }}{4}\,d_5=-\left(628+9 \gamma +6 \gamma ^2\right) \sqrt{\pi }-24 \pi ^2+\pi ^{5/2}+16 \left(3 P^2+2 P+84\right)$$ $$3 \sqrt \pi\,d_6=-4 \left(-6 (106+(\gamma -1) \gamma ) \sqrt{\pi }-24 \pi ^2+\pi ^{5/2}+48 \left(P^2+28\right)\right)$$ where $P=\psi \left(\frac{3}{2}\right)=2-\gamma -2\log (2)$

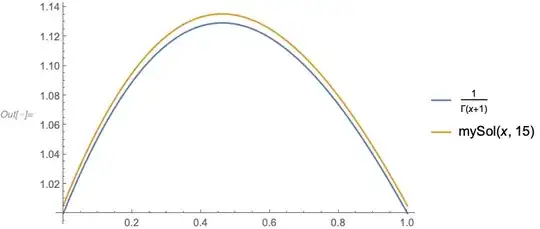
The maximum absolute error is $1.5 \times 10^{-8}$ which seems to be decent.

Making the numbers rational, this would give $$\frac{1}{\Gamma(x+1)}\sim 1+x(1-x) P_6(x)$$ $$P_6(x)=\frac{2807}{4863}-\frac{247}{3140}x-\frac{461 }{3820}x^2+\frac{66 }{1435}x^3+\frac{11 }{3303}x^4-\frac{15 }{2726}x^5+\frac{3 }{2750}x^6$$

A few values of the definite integral (just for comparison) $$\left( \begin{array}{cccc} \mu & t & \text{approximation} & \text{exact} \\ 0.25 & 0.2 & 0.182857067200 & 0.182857068268 \\ 0.25 & 0.4 & 0.329965795201 & 0.329965797571 \\ 0.25 & 0.6 & 0.443007596935 & 0.443007599310 \\ 0.25 & 0.8 & 0.526656210875 & 0.526656212492 \\ 0.25 & 1.0 & 0.586607844050 & 0.586607845209 \\ & & & \\ 0.50 & 0.2 & 0.195704099746 & 0.195704100926 \\ 0.50 & 0.4 & 0.376453536397 & 0.376453539149 \\ 0.50 & 0.6 & 0.535922898037 & 0.535922900791 \\ 0.50 & 0.8 & 0.671420159082 & 0.671420160584 \\ 0.50 & 1.0 & 0.782934567076 & 0.782934567750 \\ & & & \\ 0.75 & 0.2 & 0.203784473259 & 0.203784474510 \\ 0.75 & 0.4 & 0.407825165336 & 0.407825168343 \\ 0.75 & 0.6 & 0.602995831714 & 0.602995834721 \\ 0.75 & 0.8 & 0.782793915893 & 0.782793917219 \\ 0.75 & 1.0 & 0.943235581611 & 0.943235581767 \end{array} \right)$$

I am more than happy with these results but,again, just for the art for art's sake, I would like to be even better. For sure, I could use $p=9$ and obtain the parameters in order to match the function, first, second and third derivative values at $x=0$, $x=\frac 12$ and $x=1$; this would lead to monstreous expressions.

So, my question is : without any curve fit and avoiding so many terms, is there a way to obtain a better (mathematically based) approximation of $\Big[\Gamma(1+x)\Big]^{-1}$ for $0 \leq x \leq 1$

Answer 1

$\newcommand{\bbx}[1]{\,\bbox[15px,border:1px groove navy]{\displaystyle{#1}}\,} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\ic}{\mathrm{i}} \newcommand{\mc}[1]{\mathcal{#1}} \newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\on}[1]{\operatorname{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$ \begin{align} &\bbox[5px,#ffd]{1 \over \Gamma\pars{x + 1}} = {1 \over x!} = {x + 1 \over \pars{x + 1}!} = {\pars{x + 2}\pars{x + 1} \over \pars{x + 2}!} \\[5mm] = &\ \cdots = {\prod_{k = 1}^{n}\pars{x + k} \over \pars{x + n}!} \\[5mm] \approx &\ {\prod_{k = 1}^{n}\pars{x + k} \over \root{2\pi}\pars{x + n}^{x + n + 1/2}\,\,\,\expo{-n - x}} = {\tt mySol}\pars{x,n} \end{align}

Answer 2

My try : we have on $x\in[1,2]$ :

$$1+4(x-1)(x-2)\left(1-\Gamma\left(\left(\frac{\left(1+\sqrt{2}\right)}{2}\right)^{2}\right)\right)\simeq \Gamma(x)$$

It's not really tight but it's simple in the form.

Hope it helps you Claude.

Edit :

Around $x=2$ we have :

$$\Gamma(x)\simeq ((1-x)\frac{1}{2}(\gamma-1)+1+\frac{1}{2}(\gamma-1))^x$$

Edit 2:

Using the inverse function of the Lambert's function and denotes by :

$$g(x)=\left(1+\frac{1}{2}xe^x\right)^{x+1}$$

We have $1\leq x \leq 2$:

$$\Gamma(x)\simeq (g(1-x))^x$$

---

---

We have on $(-1,0)$ the approximation :

$$(\operatorname{W}(-ex))^{(\operatorname{W}(-x))^{1.45}}\simeq (\Gamma(1-x))^{\frac{1}{1-x}}$$

---

---

For $1\leq x\leq 2$ it seems we have the inequality :

$$f(x)=\left(\Gamma(x)\tanh(x)\right)^{\frac{2}{x(1+\tanh(e^{-1}x))}}$$

$$f(x)\leq \frac{f(1)-f(2)}{-1}(x-1)+f(1)$$

And the difference is less than $1*10^{-3}$

Last edit :

$$f(x)=\left(\Gamma(x)\tanh(x)\right)^{\frac{2}{x(1+\tanh(0.25x))}}$$

For $1\leq x\leq 2$ it seems we have the inequality :

$$(f(x))''>0$$

So we can get using convexity an arbitrary accuracy following the lenght of the interval .

Answer 3

Letting $x!=\Gamma(x+1)$, the Gamma function may be defined through the following limit for an arbitrary $\alpha$ where $x\approx0$ and $x\approx\alpha^2$ for $\alpha\approx1$ are most accurate:

$$x!=\lim_{n\to\infty}\left(n+\alpha\right)^x\prod_{k=1}^n\left(1+\frac xk\right)^{-1}$$

which has simple inverse given by

$$x!^{-1}=\lim_{n\to\infty}\left(n+\alpha\right)^{-x}\prod_{k=1}^n\left(1+\frac xk\right)$$

In the given problem, this leads to an integrand of the form $P(x)\phi^x$ for polynomial $P$ and constant $\phi$, which can be evaluated elementarily.

It's also worth pointing out that refining the estimate by taking larger $n$ does not involve a lot of recalculation since it is just one additional term on the product. However, the convergence is not very fast.

Choosing something such as $\alpha=0.9$ should lead to a good balance of over- and under-estimates of the Gamma function.

Answer 4

This answer is curve fitting, but it involves only 3 parameters. The accuracy is better than 0.13% over all $0<x<1$; good, but nothing like Claude's 8 digits or so. The idea is that the local max is not exactly at 1/2, as implied the factor $x(1-x)$ in Claude's analysis.

$$ \frac{1}{\Gamma(1+x)} \approx 1+ A \ x^b (1-x)^c $$ $$ A=0.538 , \ b=0.971 ,\ c=1.095 $$

The error is close to minimax; that is, the amplitudes of the difference curve are approximately equal.

Answer 5

What is below is exactly what I do not want to do. It is just posted to show that high order polynomials are highly significant.

What I did was to generate $10001$ equally spaced data points of $$f(x)=\frac{1}{(x-1) x}\left(\frac{1}{\Gamma (x+1)}-1\right)\qquad \qquad -\gamma \leq f(x) \leq -1+\gamma$$ using high precision.

Then, polynomial regressions; below is an example of the results for a polynomial of degree $9$ (it leads to maximum absolute errors $\sim 10^{-11}$).

$$\begin{array} \text{ } & \text{Estimate of } d_k & \sigma\text{ for }d_k \\ 1 & -0.5772156649 & 2.449\times 10^{-13} \\ x & +0.0786624078 & 1.399\times 10^{-11} \\ x^2 & +0.1206650090 & 2.600\times 10^{-10} \\ x^3 & -0.0458731951 & 2.221\times 10^{-9} \\ x^4 & -0.0036781095 & 1.028\times 10^{-8} \\ x^5 & +0.0059542170 & 2.790\times 10^{-8} \\ x^6 & -0.0012903855 & 4.563\times 10^{-8} \\ x^7 & -0.0000841706 & 4.421\times 10^{-8} \\ x^8 & +0.0000893923 & 2.336\times 10^{-8} \\ x^9 & -0.0000138358 & 5.183\times 10^{-9} \end{array}$$

Edit

In view of these results, I made the calculations for $p=9$ matching the function, first, second and third derivative values at $x=0$, $x=\frac 12$ and $x=1$; this effectively leads to monstrous expressions (I shall not type them but they are available); as one could expect, the same constants plus $\zeta(3)$ appear in their expressions. The maximum absolute error is $1.1 \times 10^{-11}$.

Now, the same table as before $$\left( \begin{array}{cccc} \mu & t & \text{approximation} & \text{exact} \\ 0.25 & 0.2 & 0.182857068266992 & 0.182857068267690 \\ 0.25 & 0.4 & 0.329965797569747 & 0.329965797571307 \\ 0.25 & 0.6 & 0.443007599308124 & 0.443007599309699 \\ 0.25 & 0.8 & 0.526656212489610 & 0.526656212491646 \\ 0.25 & 1.0 & 0.586607845206624 & 0.586607845208931 \\ & & & \\ 0.50 & 0.2 & 0.195704100925464 & 0.195704100926239 \\ 0.50 & 0.4 & 0.376453539146954 & 0.376453539148764 \\ 0.50 & 0.6 & 0.535922900789419 & 0.535922900791250 \\ 0.50 & 0.8 & 0.671420160581682 & 0.671420160584277 \\ 0.50 & 1.0 & 0.782934567746625 & 0.782934567749710 \\ & & & \\ 0.75 & 0.2 & 0.203784474509130 & 0.203784474509953 \\ 0.75 & 0.4 & 0.407825168340619 & 0.407825168342596 \\ 0.75 & 0.6 & 0.602995834719402 & 0.602995834721404 \\ 0.75 & 0.8 & 0.782793917216033 & 0.782793917219063 \\ 0.75 & 1.0 & 0.943235581763057 & 0.943235581766778 \end{array} \right)$$

Answer 6

Partial second answer.

Inspired by @FelixMarin's answer I found :

Let $2/3<x<1$ and define :

$$f\left(x\right)=\sqrt{2\pi x}\left(\frac{x}{e}\right)^{x}e^{\frac{1}{12x+\left(e-2\right)x^{-x}\cdot2^{-x}-\left(e-2\right)x^{x^{x}}+1-C}}$$

Where $C$ is the Catalan's constant .

Then it seems we have :

$$0<\frac{f\left(x\right)}{f\left(1\right)}-x!<8*10^{-5}$$

Answer 7

Hi Claude I find the following nice:

Let $x\in(0,1)$ and

$$f(x)=x!^{\frac{1}{x-1}},\quad g(x)=\frac{ f(0)-f(1) }{-1}\left(x-1\right)+f(1)+\sum_{n=1}^{\infty}\ln\left(1+\frac{x^{2n}\left(1-x\right)^{2n}}{\left(2\pi\right)^{n}}\right).$$

Then $k=10$

$$\left(g(x)\right)^{x-1}+k-\sum_{n=1}^{k}\exp\left(\frac{x^{\frac{4}{\pi}}\left(1-x\right)^{8+n}}{8^{2}}\right)>x!$$