Integral over domain of infinite tetration of x over extended domain from 0 to $\sqrt[e]e$. Possible $\int_{e^{-e}}^{e^\frac1e} x^{x^{…}}dx$ solution.

Question

I have been trying to find an interesting constant over the domain of the infinite tetration of x and have just almost figured out the area with a non integral infinite sum representation. Just one constant is in my way. D denotes the domain. This question is different from this one as it has the full domain such that the imaginary part is $0$ and not for a single point. Here is a demo of my expansion. Here is my source for the product logarithm/W-Lambert function series. My inspiration for the series is here.

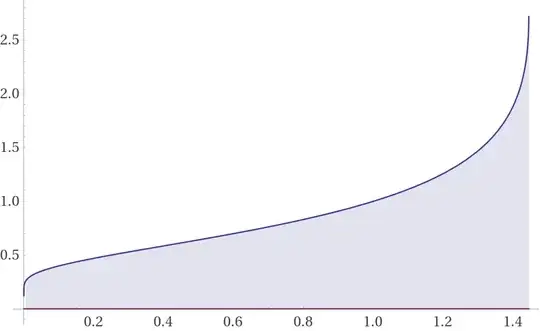
Finally here is a graph of the constant. My work is as follows. I used a bit of software to help with the evaluation at the end. Here is data about the generalized incomplete gamma function used here.

$$ \mathrm{G=\int_D x^{x^{x^…}}dx=\int_D {^\infty x}\, dx=\int_D-\frac{W(-ln(x))}{ln(x)}dx= 1.265188689361227081430914184615901039501069191363542653701819999950085943915822836313002058708863484…\implies G+\int_0^{\sqrt[-e]e }\frac {W(-ln(x))}{ln(x)}dx= \int_{\sqrt[-e]e}^{\sqrt[e]e}\frac {W(-ln(x))}{ln(x)}dx= \sum_{n=1}^\infty\frac{n^{n-1}}{n!} \int_{\sqrt[-e]e}^{\sqrt[e]e} ln^{n-1}(x)dx= \sum_{n=1}^\infty\frac{(-n)^{n-1}}{n!}Γ\left(n,-\frac 1e,\frac 1e\right)=\sum_{n=1}^\infty\frac{(-n)^{n-1}}{n}Q\left(n,-\frac 1e, \frac 1e\right)= 0.886369135921835965080748…=G-0.378819553439391116350165…} $$

I have also found the amazing result of being able to integrate the $\mathrm{x^{th}}$ root of x using a theorem on the integral of an inverse function. Here is my work.

$$\mathrm{\int_{eW\left(\frac 1e\right)}^e \left(x^\frac 1x=\sqrt[x]x\right)dx+\int_{e^{-\frac 1e}}^{e^\frac 1e} {^\infty x}\,dx=e^{1+\frac1e}-e^{1-\frac1e} W\left(\frac 1e\right)=e^{1-\frac1e}\left(e^\frac2e-W\left(\frac 1e\right)\right)=e^{1+\frac1e}\left(1-e^{-\frac2e}W\left(\frac 1e\right)\right)\implies \int_{eW\left(\frac 1e\right)}^e x^\frac 1xdx= e^{1+\frac1e}-e^{1-\frac1e} W\left(\frac 1e\right)-\sum_{n=1}^\infty\frac{(-n)^{n-1}}{n}Q\left(n,-\frac 1e, \frac 1e\right)}$$

In order to find an exact form of G, I need to find the following. The other form uses the following identity here: $$\mathrm{I= \int_0^ {e^{-\frac 1e}} x^{x^{x^…}}dx=\int_0^{e^{-\frac 1e}} {^\infty x}\, dx=\int_0^ {e^{-\frac 1e}} -\frac{W(-ln(x))}{ln(x)}dx=e^{1-\frac1e}W\left(\frac1e\right)-\int_0^ {eW\left(\frac1e\right)} \sqrt[x]x dx=0.378819553439391116350165…}$$

The previous result is proof of the following. I guess this link here is not accurate anymore. I will give an example if wanted of this result. Using another Wikipedia theorem proves that: $$\mathrm{\int x^{\frac1x}dx=x^{\frac1x+1}+\sum_{n=1}^\infty (-1)^nn^{n-2} Q\left(n,-\frac{ln(x)}{x}\right)+C,eW\left(\frac1e\right)\le x\le e}$$

more info on this result

I found this series based on this answer from @mathphile which does not give the right result as the n=0 term diverges and even trying to use the lower integration bound as $e^{-e}$ still gives the wrong result. The user’s answer would have cracked the question.

How do I evaluate this integral? A closed form is wanted, but optional. Please give me any hints as the already used series expansion for this other integral is not in the interval of convergence. This is the main constant that I need to find. Also, please correct me and give me feedback!

Note:

These Taylor series expansions were found:

Taylor Series

Unfortunately, it seems like there may be uneven radiuses of convergence which may make us need to have multiple series. Also see nth derivative of xth root of x at x=1 OEIS which has an actual formula. We are so close to the answer.

Answer 1

Note that the following method may not work for $0\le x\le e^{-e}$, but should work for convergence interval of the infinite tetration function. This interval is ${e^{-e}}\le x\le {\sqrt[e]e}, \frac1e\le y\le e$:

Although there exist a few techniques for finding a series representation, or related method, to evaluate, this one seems easiest. Graphical visualization of the result. Unfortunately, the integral from 0 to $e^{-e}$ seems to be out of the interval of convergence which is the lower convergence bound of the infinite tetration function. Here is the area under the converging original infinite tetration of x. Let this constant be denoted as $\mathrm G^*$. This leaves the only integral to be found being the following which uses the inverse function theorem mentioned in the question:

$$\mathrm{\int_{e^{-e}}^{\sqrt[-e]e}\,^\infty x\,dx=e^{1-\frac1e}W\left(\frac 1e\right)-e^{-1-e}-\int_{\frac1e}^{e W\left(\frac 1e\right)}\sqrt[x]x\, dx}$$

Let the focus be on the main integral for simplicity. The series representation uses nth derivative formulas from A008405 from the OEIS and $\mathrm{S_{x}^{(y)}}$ as the Stirling Numbers of the First Kind:

$$\mathrm{\int_{\frac1e}^{e W\left(\frac 1e\right)}\sqrt[x]x\, dx= \int_{\frac1e}^{e W\left(\frac 1e\right)}\sum_{n=0}^\infty\frac{\frac{d^n}{dx^n}\left(x^\frac1x\right)_{x=1}}{n!}(x-1)^n\,dx= \sum_{n=0}^\infty\frac{1}{n!}\sum_{m=0}^n S^{(m)}_n\sum_{k=0}^m (-k)^{m-k}\binom mk \int_{\frac1e}^{e W\left(\frac 1e\right)}(x-1)^n\,dx= \sum_{n=0}^\infty\frac{1}{(n+1)!}\sum_{m=0}^n S^{(m)}_n\sum_{k=0}^m (-k)^{m-k}\binom mk \left[\left(e W\left(\frac 1e\right)-1\right)^{n+1}-\left(\frac1e-1\right)^{n+1}\right]= \left(1-\frac1e\right)\sum_{n=0}^\infty\frac{1}{(n+1)!}\sum_{m=0}^n S^{(m)}_n\sum_{k=0}^m (-1)^{k+m+n}k^{m-k}\binom mk \left(1-\frac1e\right)^n-\left(1-eW\left(\frac1e\right)\right)\sum_{n=0}^\infty\frac{1}{(n+1)!}\sum_{m=0}^n S^{(m)}_n\sum_{k=0}^m (-1)^{k+m+n}k^{m-k}\binom mk \left(1-eW\left(\frac1e\right)\right)^n}=.35776216…$$

Note that the sum can be simplified by splitting it, manipulating the alternating part of the sum, and using special functions. Also note that the interval of convergence may be larger for the OEIS expansion. This makes it possible to split the original integral, for example, from $\mathrm{[e^{-e},1]\ to\ [1,e]}$ to get a simpler answer for the area under the infinite tetration function than the answer here. The technique would use the 2 different sum representations seen in this question and answer.

Putting this all together gives the area under the infinite tetration curve, the version not defined by the W-Lambert function, as:

$$\mathrm{G^*=\int_{e^{-e}}^{e^{-\frac1e}}\,^\infty x\,dx+ \int_{e^{-\frac1e}}^{e^{\frac1e}}\,^\infty x\,dx=\int_{e^{-e}}^{e^{\frac1e}} x^{x^…} dx= e^{1-\frac1e}W\left(\frac 1e\right)-e^{-e-1}-\sum_{n=1}^\infty\left[\frac{\left[\left(e W\left(\frac 1e\right)-1\right)^n-\left(\frac1e-1\right)^n\right]}{n!}\sum_{m=0}^{n-1} S^{(m)}_{n-1}\sum_{k=0}^m (-k)^{m-k}\binom mk +\frac{(-n)^{n-1}}{n}Q\left(n,-\frac 1e, \frac 1e\right)\right]= e^{1-\frac1e}W\left(\frac 1e\right)-e^{-1-e}-\sum_{n=1}^\infty \left[\frac{1}{n!}\left(\left[\left(e W\left(\frac 1e\right)-1\right)^n-\left(\frac1e-1\right)^n\right]\left(\frac{d^{n-1}}{dx^{n-1}}x^\frac1x\right)_{x=1}+(-n)^{n-1}Γ\left(n,-\frac 1e, \frac 1e\right)\right)\right]= 1.244131300651…}$$

Using similar techniques one can split the integral on the aforementioned interval of $[e^{-e},1] ∪ [1,e] $ as these match the convergence intervals. It uses the Lower Regularized Incomplete Gamma function denoted P(a,z):

$$\mathrm{G^*=1-e^{-e-1}+\sum_{n=0}^\infty \frac{\left(\frac{d^n}{dx^n} x^\frac1x\right)_{x=1}\left(\frac1e-1\right)^{n+1}}{n!}+\sum_{n=1}^\infty (-1)^n n^{n-2}Q\left(n,-\frac1e,0\right)= 1-e^{-e-1}-\sum_{n=1}^\infty (-1)^n\left[n^{n-2}P\left(n,-\frac1e\right)-\sum_{m=0}^{n-1}\sum_{k=0}^m \binom mk\frac{S_{n-1}^{(m)} \left(1-\frac1e\right)^n}{ (-k)^{k-m} n!}\right]= 1.244131300651437208…}$$

As the main sum has been partly shown to converge, our next goal is to find $$\mathrm{-\int_0^{e^{-e}}\frac{W(-ln(x))}{ln(x))} =e^{-e-1}-\int_0^{\frac 1e} x^\frac1x dx=.02105…}$$ in order to complete the integral in the question. However, that is for another time. Simplification would be appreciated. Please correct me and give me feedback!

Answer 2

We can have another approach for your constant $G^{*}$ in your answer:-

$\textstyle\displaystyle{-\int\frac{W(-\ln(x))}{\ln(x)}dx}$

Substitute, $u=-\ln(x)$ then $dx=-e^{-u}du$, so

$\textstyle\displaystyle{-\int\frac{W(u)}{u}e^{-u}du}$

$\textstyle\displaystyle{=-\int\frac{W(u)}{u}\sum_{n=0}^{\infty}\frac{(-1)^nu^n}{n!}du}$

$\textstyle\displaystyle{=-\int\frac{W(u)}{u}du-\sum_{n=1}^{\infty}\frac{(-1)^n}{n!}\int u^{n-1}W(u)du}$

$\textstyle\displaystyle{=-\frac{1}{2}W(u)(W(u)+2)-\sum_{n=1}^{\infty}\frac{(-1)^n}{n!}\int u^{n-1}W(u)du}$

Let's do the integral in the sum first,

$\textstyle\displaystyle{\int u^{n-1}W(u)du}$

Substitute, $v=W(u)$ then $du=(v+1)e^vdv$. So,

$\textstyle\displaystyle{\int v^ne^{nv}(v+1)dv}$ $\textstyle\displaystyle{=\int v^{n+1}e^{nv}dv+\int v^ne^{nv}dv}$

Finally substitute $t=-nv$ then $dv=-\frac{1}{n}dt$, so

$\textstyle\displaystyle{\frac{(-1)^{n}}{n^{n+2}}\int t^{n+1}e^{-t}dt+\frac{(-1)^{n+1}}{n^{n+1}}\int t^ne^{-t}dt}$

$\textstyle\displaystyle{=\frac{(-1)^{n+1}\Gamma(n+2,t)}{n^{n+2}}+\frac{(-1)^{n}\Gamma(n+1,t)}{n^{n+1}}}$

$\textstyle\displaystyle{=\frac{(-1)^n}{n^{n+1}}\left(\Gamma(n+1,-nW(u))-\frac{1}{n}\Gamma(n+2,-nW(u))\right)}$

So finally,

$\textstyle\displaystyle{-\int\frac{W(u)}{u}e^{-u}du}$

$\textstyle\displaystyle{=-\frac{1}{2}W(u)(W(u)+2)-\sum_{n=1}^{\infty}\frac{1}{n!n^{n+1}}\left(\Gamma(n+1,-nW(u))-\frac{1}{n}\Gamma(n+2,-nW(u))\right)}$

Then the definite integral would be-

$\textstyle\displaystyle{-\int_{e^{-e}}^{e^\frac{1}{e}}\frac{W(-\ln(x))}{\ln(x)}dx}$

$\textstyle\displaystyle{=\bigg[-\frac{1}{2}W(-\ln(x))(W(-\ln(x))+2)-\sum_{n=1}^{\infty}\frac{1}{n!n^{n+1}}\left(\Gamma(n+1,-nW(-\ln(x)))-\frac{1}{n}\Gamma(n+2,-nW(-\ln(x)))\right)\bigg]_{e^{-e}}^{e^\frac{1}{e}}}$

$\textstyle\displaystyle{G^{*}=2+\sum_{n=1}^{\infty}\frac{1}{n!n^{n+1}}\left(\frac{1}{n}\Gamma(n+2,n)-\Gamma(n+1,n)\right)+\sum_{n=1}^{\infty}\frac{1}{n!n^{n+1}}\left(\Gamma(n+1,-n)-\frac{1}{n}\Gamma(n+2,-n)\right)}$

We can simplify this using the generalized incomplete function-

$\Gamma(x,y)-\Gamma(x,z)=\Gamma(x,y,z)$

And then using the recurrence relation which can be easily obtained through integration by parts-

$\Gamma(a,b,c)$

$=b^{a-1}e^{-b}-c^{a-1}e^{-c}+(a-1)\Gamma(a-1,b,c)$

So,

$\textstyle\displaystyle{G^{*}=2-\sum_{n=1}^{\infty}\frac{1}{n!n^{n+1}}\left(\frac{1}{n}\Gamma(n+2,-n,n)-\Gamma(n+1,-n,n)\right)}$

$\textstyle\displaystyle{=2-\sum_{n=1}^{\infty}\frac{1}{n!n^{n+1}}\left((-1)^{n+1}n^ne^n-n^ne^{-n}+\frac{1}{n}\Gamma(n+1,-n,n)\right)}$

$\textstyle\displaystyle{=2-\sum_{n=1}^{\infty}\left(-\frac{e^{-n}}{n!n}-\frac{(-e)^n}{n!n}+\frac{1}{n!n^{n+2}}\Gamma(n+1,-n,n)\right)}$

From here and here we can simplify even further-

$\textstyle\displaystyle{G^{*}=\int_{e^{-e}}^{e^\frac{1}{e}}{^{\infty}x}dx}$

$\boxed{\textstyle\displaystyle{G^{*}=2-2\gamma+\operatorname{Ei}(-e)+\operatorname{Ei}\left(\frac{1}{e}\right)-\sum_{n=1}^{\infty}\frac{\operatorname{Q}(n+1,-n,n)}{n^{n+2}}}}$

I can't simplify more than this.

---

---

For the last integral in your answer, I think I can give you a sum using the lagrange inversion theorem-

Let, $f(x)=x^\frac{1}{x}$

Then,

$\textstyle\displaystyle{\begin{align}f^{-1}(x)&=e^{-W(-\ln(x))}\\&=-\frac{W(-\ln(x))}{\ln(x)}\end{align}}$

Using the Lagrange Inversion theorem we have

$\textstyle\displaystyle{x^\frac{1}{x}=1+\sum_{n=1}^{\infty}f_n\frac{(x-1)^n}{n!}}$

Where, $\textstyle\displaystyle{f_n=\lim_{h\rightarrow 1}\frac{d^{n-1}}{dh^{n-1}}\left[\left(\frac{h-1}{e^{-W(-\ln(h))}-1}\right)^n\right]}$

Here I have taken $a=1$

By the ratio test we have the radius of convergence for the sum-

$\textstyle\displaystyle{\lim_{n\rightarrow\infty}\left|\frac{a_{n+1}}{a_n}\right|}$

$\textstyle\displaystyle{=\lim_{n\rightarrow\infty}\left|\frac{f_{n+1}\frac{(u-1)^{n+1}}{(n+1)!}}{f_n\frac{(u-1)^n}{n!}}\right|}$

$\textstyle\displaystyle{=|u-1|\lim_{n\rightarrow\infty}\left|\frac{f_{n+1}}{(n+1)f_n}\right|<1}$

$\implies\textstyle\displaystyle{|u-1|<\lim_{n\rightarrow\infty}\left|\frac{(n+1)f_n}{f_{n+1}}\right|}$

I don't really know how to calculate $f_n$ cause wolfram alpha doesn't give me an answer when $n>3$. So unless I have an easily manageable formula for $f_n$, I don't know what the limit is, so I would ask for help in that.

So, assuming that the bounds of the integral are within the radius of convergence,

$\textstyle\displaystyle{\int_{0}^{\frac{1}{e}}x^\frac{1}{x}dx}$

$\textstyle\displaystyle{=\int_{0}^{\frac{1}{e}}\left(1+\sum_{n=1}^{\infty}f_n\frac{(x-1)^n}{n!}\right)dx}$

$\textstyle\displaystyle{=\int_{0}^{\frac{1}{e}}dx+\sum_{n=1}^{\infty}\frac{f_n}{n!}\int_{0}^{\frac{1}{e}}(x-1)^ndx}$

$=\boxed{\textstyle\displaystyle{\frac{1}{e}+\sum_{n=1}^{\infty}\frac{(-1)^{n}f_n}{(n+1)!}\left(1-\left(1-\frac{1}{e}\right)^{n+1}\right)}}$

$\{f_n\}_{n=1}^{\infty}$

$=\{1,-2,3,\dots\}$

If I am able derive more about $f_n$ then I will add it to the answer.

---

---

Finally if your derivation in the answer is correct then,

$\textstyle\displaystyle{G=G^{*}-\int_{0}^{e^{-e}}\frac{\operatorname{W}(-\ln(x))}{\ln(x)}dx}$

$\textstyle\displaystyle{=e^{-1-e}+G^{*}-\int_{0}^{\frac{1}{e}}x^\frac{1}{x}dx}$

$\textstyle\displaystyle{=2-2\gamma+e^{-1-e}-\frac{1}{e}+\operatorname{Ei}(-e)+\operatorname{Ei}\left(\frac{1}{e}\right)-\sum_{n=1}^{\infty}\frac{\operatorname{Q}(n+1,-n,n)}{n^{n+2}}-\sum_{n=1}^{\infty}\frac{(-1)^nf_n}{(n+1)!}\left(1-\left(1-\frac{1}{e}\right)^{n+1}\right)}$

Which looks really messy but that's all I can give you for now.

To be honest I prefer the constant $G^{*}$ better than $G$.

$\text{Conclusion:-}$

$\boxed{\textstyle\displaystyle{G=2-2\gamma+e^{-1-e}-\frac{1}{e}+\operatorname{Ei}(-e)+\operatorname{Ei}\left(\frac{1}{e}\right)-\sum_{n=1}^{\infty}\frac{\operatorname{Q}(n+1,-n,n)}{n^{n+2}}-\sum_{n=1}^{\infty}\frac{(-1)^nf_n}{(n+1)!}\left(1-\left(1-\frac{1}{e}\right)^{n+1}\right)}}$

Where,

$\textstyle\displaystyle{f_n=\lim_{h\rightarrow 1}\frac{d^{n-1}}{dh^{n-1}}\left[\left(\frac{h-1}{e^{-W(-\ln(h))}-1}\right)^n\right]}$