How can I prove that $xy\leq x^2+y^2$ for all $x,y\in\mathbb{R}$ ?
-
8Note that you will need $(x, y) \neq (0, 0)$, to show the strict inequality. – Calvin Lin Apr 10 '13 at 16:28
-
3@Maesumi In fact, you need $x\neq y$ for the strict inequality. – Douglas B. Staple Apr 10 '13 at 19:09
-
9You can easily prove that $|xy|\leq \left(\mbox{max}{|x| , |y| }\right)^2$. – N. S. Apr 11 '13 at 17:50
-
3You also need $x$ and $y$ to be real, since it is false for $x = y = i$. – marty cohen Apr 15 '13 at 14:32
-
34Is this a competition for the most complicated answer? 0_o What the hell is wrong with you, people? – Aleksei Averchenko Apr 15 '13 at 15:24
-
1This is the first page I have seen, with such a wide variety of inequality tricks. Taught me more than a book :). – Sawarnik Feb 16 '14 at 15:43
-
See also: Prove the inequality $|xy|\leq\frac{1}{2}(x^2+y^2)$ and Show that $2 xy < x^2 + y^2$ for $x$ is not equal to $y$, – Martin Sleziak Dec 09 '18 at 08:54
25 Answers
Use polar coordinates: $$x=r \cos \theta,y=r \sin \theta $$
Your inequality becomes $$r^2 \cos \theta \sin \theta \leq r^2 $$
which is pretty much trivial.
- 24,381
-
14+1 cos i like this unnecessary overkill :D I don't know if this, or the question is more elementary... – Lost1 Apr 10 '13 at 16:47
-
But you make both $x,y$ bound . ie. less than $r$ and even related to each other . $x^2+y^2=r^2$ .They become the co-ordinates of a circle! – ABC Apr 10 '13 at 16:49
-
2@exploringnet I don't see a problem. Any point in the plane has its polar coordinates. The radius $r$ is definitely not constant! – user1337 Apr 10 '13 at 17:06
-
Ok but till x,y are related to each other by this . But we have no such relation., x,y must be independent – ABC Apr 10 '13 at 17:08
-
6@exploringnet and they are. This relationship doesn't make them dependent. – user1337 Apr 10 '13 at 17:13
-
-
I'm not sure I understand what you mean by dependent then, and why does that interfere with the proof. Can we move this discussion to chat? – user1337 Apr 10 '13 at 17:20
-
-
6@exploringnet: They're not dependent; it's not determined that $x = r/2$ until $y$ is known. – LarsH Apr 11 '13 at 07:58
\begin{align} 0\leq (x-y)^2 \implies & 0\leq x^2-2xy +y^2 \\ \implies & 2xy\leq x^2+y^2 \\ \implies & xy\leq \dfrac{x^2+y^2}{2} \\ \implies & xy\leq {x^2+y^2} \end{align} since the clearly nonnegative real $x^2+y^2$ clearly satisfies $\dfrac{x^2+y^2}{2} \leq x^2+y^2$.
- 17,777
- 14,658
Though there are quite a few proofs already given, I'd like to add a visual one.
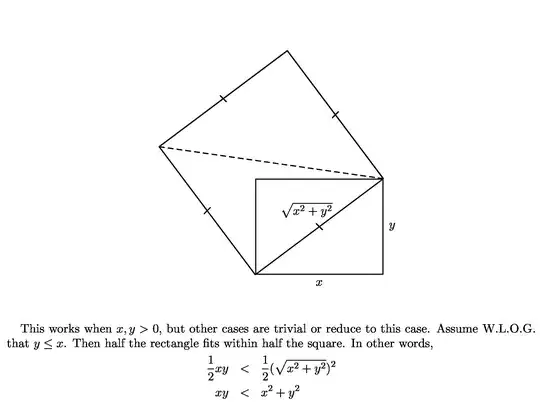
- 75,051
- 8,871
-
1
-
3@Ruslan: Sorry, I should have cropped it. I used Latex with pstricks and generated a page of output. – Shaun Ault Apr 10 '13 at 17:54
-
1
-
-
How do you prove $y\le x$ says that half the rectangle fits withing half the square? – maxuel Jan 16 '15 at 10:02
Another interesting answers - maybe the most interesting:
$$x^2+y^2-xy=\left(x-\frac{y}{2}\right)^2+\frac{3y^2}{4} \geq 0.$$
- 6,790
A proof with only words: assume $x$ and $y$ are positive, if one is negative this is trivial. Then one of $x$ or $y$ is smallest, the other largest. Assume $y$ is the largest (else switch). Then $xy$ is clearly less than $y^2$, and adding $x^2$ doesn't change that!
- 172,925
- 6,625
-
4I like proofs with only words. :-) This answer has been the most accessible one for me. You might want to mention the case where $x$ and $y$ are both negative, though. – LarsH Apr 11 '13 at 07:42
For $xy<0$, this is trivial
You can do better by proving $2xy \leq x^2 + y^2$. Move $2xy$ to the right handside and factorise
- 7,895
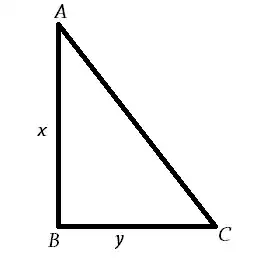
$x^2+y^2=AC^2$
$\sin \angle BAC= \dfrac{BC}{AC}$
$\sin \angle BCA= \dfrac{AB}{AC}$
$\sin \angle BCA \cdot \sin \angle BAC <1 \implies \dfrac{xy}{x^2+y^2} <1$.
- 7,881
$$(x^2 - xy + y^2)(x + y) = x^3 + y^3.$$ $x^3 + y^3$ and $x + y$ have the same sign: $x \leq -y$ iff $x^3 \leq -y^3$. Therefore, $x^2 - xy + y^2 \geq 0$.
About the special case $x = -y$: it’s not really that special, but for a technical reason that goes beyond precalculus. Since non-trivial Zariski open sets are dense in the Euclidean topology, and polynomial maps are continuous between Euclidean topologies, all inequalities of the form $f(x_1, \ldots, x_n) \geq 0$ (where $f$ is a polynomial) that hold on a Zariski open set must hold everywhere, because $[0, +\infty)$ is closed and its preimage must thus contain the closure of said Zariski open set, i.e. the whole space. Therefore, such apparent special cases can be safely ignored as long as they’re Zariski closed and the inequality is not strict.
- 8,023
-
5
-
2@ronno Not really, because $X := \mathbb{R}^2 \setminus {x = -y}$ is dense in $\mathbb{R}^2$, and $[0, +\infty)$ is closed in $\mathbb{R}$, therefore its pullback along $(x, y) \mapsto x^2 - xy + y^2$ must be $\operatorname{cl}X = \mathbb{R}^2$. Of course it is too technical for a precalculus-level question. – Aleksei Averchenko Aug 14 '14 at 20:18
Another one - if $xy \le 0$ it is trivial, so let $xy > 0$. Then we have $$ 1 \le \dfrac{x}{y}+\dfrac{y}{x}$$
Now for any positive number, either it or its reciprocal must exceed $1$, unless both are $1$.
- 46,381
If $xy$ is negative, then the statement is obvious since $xy < 0 \leq x^2 + y^2$.
Otherwise, $xy$ is non-negative, and we can show that $xy \leq 2xy \leq x^2+y^2$, where the latter follows from the trivial inequality $(x-y)^2 \geq 0 $.
- 68,864
Just look at this picture below:
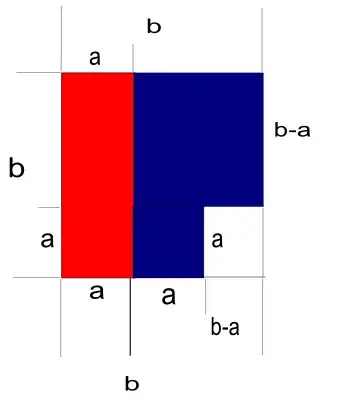
- 809
-
Trying to make sure I understand how $a, b$ relate to $x, y$. Are we to assume that $b = max(x, y)$ and $a = min(x, y)$? (And that $x, y \geq 0$.) – LarsH Apr 11 '13 at 08:02
-
You can assume that $x \leq y$ WOLOG. If $x,y \geq 0$, then treat $a$ as $x$ and $b$ as $y$. – jskattt797 Jun 28 '20 at 22:11
Intuitive Approach
if $|x|\le |y|$ then we have $$x\cdot y \le y\cdot y \le y.y + x\cdot x$$ $$\Rightarrow x\cdot y \le x^2+y^2\tag1$$ Using Symmetry $(1)$ holds if $|x|\ge |y|$
- 2,544
This is clearly a consequence of the concavity of the logarithm and the monotonicity of the exponential.
Since $xy\leq |x||y|$, we can assume that $x >0$ and $y > 0$. Then we have $$ xy = \exp(\ln(xy)) = \exp(\ln x + \ln y) = \exp(\frac12\ln x^2 + \frac12 \ln y^2) \leq \exp(\ln(\frac{x^2}2 + \frac{y^2}2)) =\frac{x^2}2 + \frac{y^2}2 \leq x^2 + y^2. $$ QED
- 201
$$x^2+y^2-xy=\frac{(2x-y)^2+3y^2}4=\frac{(2x-y)^2+(\sqrt3y)^2}4$$
Now, the square of any real numbers is $\ge0$
So, $(2x-y)^2+(\sqrt3y)^2\ge0,$ the equality occurs if each $=0$
- 274,582
-
Thanks for the down-vote. I could find a better way to prove it. – lab bhattacharjee May 10 '13 at 14:18
-
3Dear lab bhattacharjee, to be honest, I should admit that it is me who downvoted your answer earlier. I did the downvote not because your answer is not good, but personally I don't encourage users with high reputation like you to pay much attention to trivial questions like this one. In my opinion, supporting such questions will diminish the quality of this website. By the way, I also downvoted lots of other answers(to this/other post) provided by users with high reputation for the same reason. In view of your serious attitude to downvotes, I have to cancel my downvote. Sorry for bothering. – 23rd May 10 '13 at 15:57
Technique 1:$$\sqrt{x^2y^2} = xy \le \dfrac{x^2 + y^2}{2}\le x^2 + y^2$$ Technique 2:$$(x - y)^2 \ge 0 \implies x^2 +y^2 - 2xy \ge 0 \implies x^2 + y^2 \ge 2xy\ge xy$$ Technique 3 (my favorite): There's a statement $\dfrac{y}{x} + \dfrac{x}{y} \ge 2$ with many classical proofs (which I'd not state here). We can write the inequality as follows:$$\dfrac{y}{x}+\dfrac{x}{y} \ge 1$$Divide both sides by $xy$.$$\dfrac{1}{x^2} + \dfrac{1}{y^2} \ge \dfrac{1}{xy}$$Rewrite.$$\dfrac{x^2 + y^2}{x^2y^2} \ge \dfrac{xy}{x^2y^2}$$And finally...$$x^2 + y^2 \ge xy$$
- 7,742
A different approach, $$A.M[x_i^n]\ge(A.M[x_i])^n\ge GM[x_1]^n$$
ie. AM of terms with $n$th power is greater than $n$th power of AM ie. greater than $n$th power of GM . So,$$\dfrac{x^2+y^2}2\ge(\dfrac{x+y}2)^2\ge(xy)$$ and so,$$(x^2+y^2)\ge xy$$
And for $xy<0$ the inequality is obvious.
- 6,034
Assume $x$ and $y$ are positive. Draw the right triangle with vertices $(0,0), (x,0), (x,y)$. Draw the circle around $(0,0)$ that circumscribes the triangle. Reflect the triangle in the $x$-axis. Reflect the two triangles in the $y$-axis too, for a better result.
- 1,747
Let $y=kx$ then $ x xk \leq x^2 + x^2k^2$ since $k\leq k^2+1$ [in view of $0\leq (k-1/2)^2+3/4] $
And the ineq. clearly holds when $x=0$ . $\hspace {33mm} \blacksquare$
- 1,347
$$(x-y)^2=x^2+y^2-2xy\\ (x-y)^2+2xy=x^2+y^2\\ 2xy\leq x^2+y^2$$ Therefore $xy\leq x^2+y^2$. Hence the proof.
- 25,582
- 7
- 59
- 91
- 151
- 1
First, $$ a^2+3b^2\geq 0 $$ Now, $$ a^2+2ab+b^2+a^2-2ab+b^2\geq a^2-b^2 $$ Thus, $$ (a+b)^2+(a-b)^2\geq (a+b)(a-b) $$ Let $a+b=x, a-b=y$, i.e., $a=\frac{x+y}{2}, b=\frac{x-y}{2}$ which is one-to-one correspondence between $(x,y)$ and $(a,b)$, then, $$ x^2+y^2\geq xy $$ Q.E.D
- 41
$(x - y)^2 \geq 0$
$x^2 + y^2 -2xy \geq 0$
$x^2 + y^2 \geq 2xy > xy$
upate Happy Green Kid is right below, the case for xy < 0 needs to be considered:
so, continuing from:
$x^2 + y^2 \geq 2xy$
if $xy > 0:$
$x^2 + y^2 \geq 2xy > xy$
else
$x^2 + y^2 > 0 > xy$
in both cases
$x^2 + y^2 > xy$
- 6,726
- 127
If xy is negative, then it is trivial. If both x and y are negative, then let x := -x and y := -y. This means that we can safely assume that both x and y are positive.
Square each sides yields
$$x^2y^2 \le x^4 + 2x^2y^2 + y^4$$
, which trivially holds.
- 1,670
Say $y\ne 0$ then divide both sides by $y^2$; let $z=\frac{x}{y}$; then we need $z\le 1+z^2$ or equivalently $z^2-z+1\ge 0$; completing the square gives $(z-\frac{1}{2})^2+\frac{3}{4}\ge 0$ which is clear.
- 52,094
- 4,259
Let $y>=x. xy<=x^2+y^2$. Divide both sides by $y$, and you get $x<=(x^2/y)+y$. If $x$ and $y$ are both positive numbers, this is clearly true because we said from the beginning that $y>=x$.
- 23,737