Proof of $\lim_{n\to \infty} \sqrt[n]{n}=1$

Question

Thomson et al. provide a proof that $\lim_{n\rightarrow \infty} \sqrt[n]{n}=1$ in this book (page 73). It has to do with using an inequality that relies on the binomial theorem:

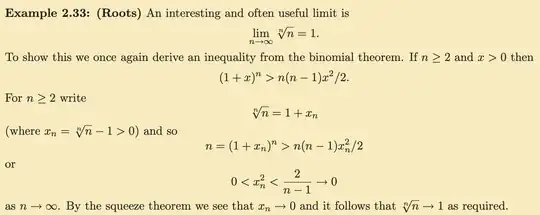
I have an alternative proof that I know (from elsewhere) as follows.

---

Proof.

\begin{align} \lim_{n\rightarrow \infty} \frac{ \log n}{n} = 0 \end{align}

Then using this, I can instead prove: \begin{align} \lim_{n\rightarrow \infty} \sqrt[n]{n} &= \lim_{n\rightarrow \infty} \exp{\frac{ \log n}{n}} \newline & = \exp{0} \newline & = 1 \end{align}

---

On the one hand, it seems like a valid proof to me. On the other hand, I know I should be careful with infinite sequences. The step I'm most unsure of is: \begin{align} \lim_{n\rightarrow \infty} \sqrt[n]{n} = \lim_{n\rightarrow \infty} \exp{\frac{ \log n}{n}} \end{align}

I know such an identity would hold for bounded $n$ but I'm not sure I can use this identity when $n\rightarrow \infty$.

Question:

If I am correct, then would there be any cases where I would be wrong? Specifically, given any sequence $x_n$, can I always assume: \begin{align} \lim_{n\rightarrow \infty} x_n = \lim_{n\rightarrow \infty} \exp(\log x_n) \end{align} Or are there sequences that invalidate that identity?

---

(Edited to expand the last question) given any sequence $x_n$, can I always assume: \begin{align} \lim_{n\rightarrow \infty} x_n &= \exp(\log \lim_{n\rightarrow \infty} x_n) \newline &= \exp(\lim_{n\rightarrow \infty} \log x_n) \newline &= \lim_{n\rightarrow \infty} \exp( \log x_n) \end{align} Or are there sequences that invalidate any of the above identities?

(Edited to repurpose this question). Please also feel free to add different proofs of $\lim_{n\rightarrow \infty} \sqrt[n]{n}=1$.

Answer 1

Here is one using $AM \ge GM$ to $1$ appearing $n-2$ times and $\sqrt{n}$ appearing twice.

$$\frac{1 + 1 + \dots + 1 + \sqrt{n} + \sqrt{n}}{n} \ge n^{1/n}$$

i.e

$$\frac{n - 2 + 2 \sqrt{n}}{n} \ge n^{1/n}$$

i.e.

$$ 1 - \frac{2}{n} + \frac{2}{\sqrt{n}} \ge n^{1/n} \ge 1$$

That the limit is $1$ follows.

Answer 2

Since $x \mapsto \log x$ is a continuous function, and since continuous functions respect limits: $$ \lim_{n \to \infty} f(g(n)) = f\left( \lim_{n \to \infty} g(n) \right), $$ for continuous functions $f$, (given that $\displaystyle\lim_{n \to \infty} g(n)$ exists), your proof is entirely correct. Specifically, $$ \log \left( \lim_{n \to \infty} \sqrt[n]{n} \right) = \lim_{n \to \infty} \frac{\log n}{n}, $$

and hence

$$ \lim_{n \to \infty} \sqrt[n]{n} = \exp \left[\log \left( \lim_{n \to \infty} \sqrt[n]{n} \right) \right] = \exp\left(\lim_{n \to \infty} \frac{\log n}{n} \right) = \exp(0) = 1. $$

Answer 3

Here's a two-line, completely elementary proof that uses only Bernoulli's inequality:

$$(1+n^{-1/2})^n \ge 1+n^{1/2} > n^{1/2}$$ so, raising to the $2/n$ power, $$ n^{1/n} < (1+n^{-1/2})^2 = 1 + 2 n^{-1/2} + 1/n < 1 + 3 n^{-1/2}.$$

I discovered this independently, and then found a very similar proof in Courant and Robbins' "What is Mathematics".

Answer 4

$\sqrt[n]{n}=\sqrt[n]{1\cdot\frac{2}{1}\cdot\frac{3}{2}\dots\cdot\frac{n-1}{n-2}\cdot\frac{n}{n-1}}$ so you have a sequence of geometric means of the sequence $a_{n}=\frac{n}{n-1}$. Therefore its limit is equal to $\lim_{n\to\infty}a_{n}=\lim_{n\to\infty}\frac{n}{n-1}=1$.

Answer 5

Let $n > 1$ so that $n^{1/n} > 1$ and we put $n^{1/n} = 1 + h$ so that $h > 0$ depends on $n$ (but we don't write the dependence explicitly like $h_{n}$ to simplify typing) Our job is done if show that $h \to 0$ as $n \to \infty$.

We have $$n = (1 + h)^{n} = 1 + nh + \frac{n(n - 1)}{2}h^{2} + \cdots$$ and hence $$\frac{n(n - 1)}{2}h^{2} < n$$ or $$0 < h^{2} < \frac{2}{n - 1}$$ It follows that $h^{2} \to 0$ as $n \to \infty$ and hence $h \to 0$ as $n \to \infty$.

Answer 6

Let $n$ be an integer $n>2$ and real $x>0$, the binomial theorem says $$ (1+x)^n>1+nx+\frac{n(n-1)}{2}x^2 $$ Let $N(x)=\max(2,1+\frac{2}{x^2})$. For $n>N(x)$, we get that $\frac{n(n-1)}{2}x^2>n$. Thus, for any $x>0$, we get that for $n>N(x)$ $$ 1<\sqrt[n]{n}<1+x $$ Thus, we have $$ 1\le\liminf_{n\to\infty}\sqrt[n]{n}\le\limsup_{n\to\infty}\sqrt[n]{n}\le 1+x $$ Since this is true for any $x>0$, we must have $$ \lim_{n\to\infty}\sqrt[n]{n}=1 $$

Answer 7

The limit follows from these inequalities and the squeeze theorem: $$ 1<n^{1/n}<1+\sqrt{\frac{2}{n-1}},\qquad n>1 $$ where the right inequality follows by keeping only the third term in the binomial expansion: $$ (1+x)^n>\binom{n}{2}x^2= n,\quad \textrm{where}\quad x^2=\frac{2}{n-1}. $$

Answer 8

Take $n=2^m$

$$\lim\limits_{n \to \infty} \sqrt[n]{n} = \lim\limits_{m \to \infty} \sqrt[2^m]{2^m}= \lim\limits_{m \to \infty} 2^{\frac{m}{2^m}}=2^{\lim\limits_{m \to \infty} \frac{m}{2^m}}=2^0=1$$

This is inverted and maybe a more obvious way from the original one.