Integral evaluation $\int_{-\infty}^{\infty}\frac{\cos (ax)}{\pi (1+x^2)}dx$

Question

Possible Duplicate:
Calculating the integral $\int_{0}^{\infty} \frac{\cos x}{1+x^2}\mathrm{d}x$ without using complex analysis

I need help to evaluate the integral of

$$\int_{-\infty}^{\infty}\frac{\cos (ax)}{\pi (1+x^2)}dx$$ where $a$ is a real number. I know the answer is $e^{-|a|}$.

I think contour integration can do the job by evaluating $e^{iaz}/(z^2+1)$ but I don't remember the details from complex analysis in college.

My question is "Is there a way to compute this integration WITHOUT using complex analysis method?" For example, by change of variables with trigonometric function, integration by part, or something like that.

Answer 1

Let $\displaystyle f(a) = \int_{0}^{\infty}\frac{\cos(ax)}{1+x^2}\;{dx}$. Consider the Laplace transform of $f(a)$.

$$\begin{aligned}\mathcal{L}(f(a)) & = \int_{0}^{\infty}\int_{0}^{\infty}\frac{\cos(ax)}{1+x^2}e^{-as}\;{da}\;{dx} \\&= \int_{0}^{\infty}\frac{s}{(1+x^2)(s^2+x^2)}\;{dx} \\& = \frac{\pi}{2(s+1)}.\end{aligned} $$

Thus $ \displaystyle f(a) =\mathcal{L}^{-1}\left(\frac{\pi}{2(s+1)}\right) =\frac{\pi}{2}e^{-|a|} $ and your integral is $\displaystyle \frac{2}{\pi}f(a) = e^{-|a|}.$

Answer 2

Write the integral as

$$\frac{1}{\pi} \int_{-\infty}^{\infty} dx \: \frac{\exp (i a x)}{ (1+x^2)}$$

which is still real because the imaginary part vanishes over the symmetric interval. Now consider the following complex integral

$$ \int_{C} dz \: \frac{\exp (i a z)}{ (1+z^2)}$$

where $C$ is the following contour for $a > 0$:

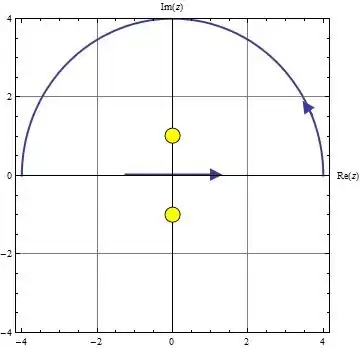
The value of this integral is equal to $i 2 \pi$ times the sum of the residues of the poles of the integrand inside $C$. These poles are at $z = \pm i$, and the residues of the integrand at these poles are

$$\mathrm{Res}_{z=\pm i} \frac{\exp (i a z)}{ (1+z^2)} = \pm \frac{\exp{(\mp a)}}{i 2}$$

For the contour $C$, only the residue at $z=i$ is inside, so the value of the integral is

$$ \int_{C} dz \: \frac{\exp (i a z)}{ (1+z^2)} = i 2 \pi \frac{\exp{(-a)}}{i 2} = \pi \exp{(-a)}$$

This integral may also be expressed in terms of the integral over the two individual components of contour $C$:

$$ \int_{C} dz \: \frac{\exp (i a z)}{ (1+z^2)} = \int_{-R}^{R} dx \: \frac{\exp (i a x)}{ (1+x^2)} + i R \int_{0}^{\pi} d \phi \: \exp{(i \phi)} \frac{\exp (i a R \exp{(i \phi)})}{ (1+R^2 \exp{(i 2 \phi)})} $$

where $R$ is the extent of $C$ along the $\Re{z}$ axis. Note that the second integral on the right-hand side results from a substitution $z = R \exp{(i \phi)}$ and corresponds to the integral along the semicircle. We take the limit as $R \rightarrow \infty$. Note that the first integral becomes the integral we seek, and we want to show that the second integral vanishes in this limit. In fact, it turns out that

$$ \left | i R \int_{0}^{\pi} d \phi \: \exp{(i \phi)} \frac{\exp (i a R \exp{(i \phi)})}{ (1+R^2 \exp{(i 2 \phi)})} \right | \approx \frac{1}{R} \int_{0}^{\pi} d \phi \: \exp{(-a R \cos{\phi})}, \: \: (R \rightarrow \infty) $$

which only converges when $a>0$; for this case, the integral vanishes as $R \rightarrow \infty$, and we can say:

$$\frac{1}{\pi} \int_{-\infty}^{\infty} dx \: \frac{\exp (i a x)}{ (1+x^2)} = \exp{(-a)} , \: \: a>0$$

When $a<0$, we flip the contour about the $\Re{z}$ axis and use the pole at $z=-i$ for the residue. In this case, we find that

$$\frac{1}{\pi} \int_{-\infty}^{\infty} dx \: \frac{\exp (i a x)}{ (1+x^2)} = \exp{(a)} , \: \: a<0$$

Combining these results and returning to the original integral expression, we get the result you sought:

$$\int_{-\infty}^{\infty} dx \: \frac{\cos(a x)}{\pi (1+x^2)} = \exp({-|a|)}$$

Answer 3

Let $$I(a) = \int_{-\infty}^{\infty} \dfrac{\cos(ax)}{\pi(1+x^2)}dx$$ $$I''(a) = -\int_{-\infty}^{\infty} \dfrac{x^2\cos(ax)}{\pi(1+x^2)}dx$$ Hence, $$I''(a)-I(a) = - \dfrac1{\pi}\int_{-\infty}^{\infty} \cos(ax) dx = f(a)$$ The Cauchy principal value of $f(a) = 0$. Hence, we get that $$I(a) = c_1e^a + c_2e^{-a}$$

Note that $$\vert I(a) \vert \leq \int_{-\infty}^{\infty} \dfrac{dx}{\pi(1+x^2)} = I(0) = \dfrac2{\pi} \arctan(2N \pi) < 1$$ If $a>0$, this implies $c_1 = 0$. Further, $I(0) = 1$ gives us $I=e^{-a}$. Now since $I(-a) = I(a)$ for $a>0$, we get that $$I(a) = e^{-\vert a \vert}$$ for all $a \in \mathbb{R}$.