I recently came across this problem in complex analysis: $$\int_0^\infty \frac{\sin mx}{x(x^2 + a^2)} ~ dx= \frac{\pi}{2a^2} \left(1-\frac{1}{e^{ma}}\right)$$ for $a,m > 0$.
I saw this somehow related integral here but I can't make the right substitution to arrive at the desired answer. I've been trying to solve this for almost 2 days straight without luck.
You can use Integral evaluation $\int_{-\infty}^{\infty}\frac{\cos (ax)}{\pi (1+x^2)}dx$ to obtain the result. In fact, let $$I(m)=\int_0^\infty \frac{\sin mx}{x(x^2 + a^2)} ~ dx.$$ Then $I(0)=0$ and $$I'(m)=\int_0^\infty \frac{\cos mx}{x^2 + a^2} ~ dx=\frac{\pi e^{-a m}}{2a}.$$ So $$ I(m)=\int_0^mI(s)ds=\int_0^m\frac{\pi e^{-a s}}{a}ds=\frac{\pi}{2a^2} \left(1-\frac{1}{e^{ma}}\right). $$
You can solve this problem by considering the similar, complex function
$$f(z)=\frac{e^{imz}}{z(z^2+a^2)}$$
integrated counterclockwise around the contour $C$ in the image below. The contour consists of a semi-circle $\Gamma$ with radius R in the upper half-plane, from which a smaller semi-cirle $\gamma$ with radius $\epsilon$, centered at the origin, has been cut out.
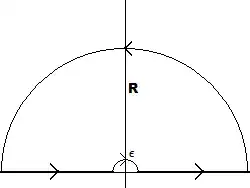
The integral around C can be split into four parts:
$$\oint_Cf(z)dz = \int_{\Gamma}f(z)dz + \int_{\gamma}f(z)dz + \int_{-R}^{-\epsilon}f(z)dz + \int_{\epsilon}^{R}f(z)dz.\tag{1}$$
The left hand side can be evaluated using the residue theorem. The only pole of $f$ which lies inside $C$ is $z=ia$, corresponding to the residue
$$Res_{z=ia}=\lim_{z\to ia}(z-ia)f(z)=\lim_{z\to ia}\frac{e^{imz}}{z(z+ia)}=-\frac{e^{-ma}}{2a^2}.$$
Then, by said theorem,
$$\oint_Cf(z)dz = 2\pi i\cdot(\text{sum of all residues}) = -\frac{\pi i}{a^2e^{ma}}.\tag{2}$$
Next, consider the first term on the right-hand side of (1). Since
$$\left|\frac{e^{imz}}{z(z^2+a^2)}\right|=\left| \frac{1}{z}\right|\left| \frac{1}{z^2+a^2}\right|\leq \frac{1}{R}\left|\frac{1}{z^2}\right|=\frac{1}{R^3},$$
then, by using the estimation lemma and taking the limit as $R$ approaches infinity, you can conclude that
$$\lim_{R\to\infty}\left| \int_{\Gamma}f(z)dz \right| \leq \lim_{R\to\infty} \frac{1}{R^3}\cdot(\text{arc length of }\Gamma) = \lim_{R\to\infty} \frac{\pi}{R^2} = 0. \tag{3}$$
The second term on the right-hand side of (1) can be calculated by substituting $z=\epsilon e^{i\theta} \to dz=i\epsilon e^{i\theta}d\theta$, where $\theta$ is the counter-clockwise angle from the positive x-axis. Note that
$$\int_{\gamma}f(z)dz=\int_{\gamma}\frac{e^{imz}}{z(z^2+a^2)}dz = \int_{\pi}^0\frac{e^{im\epsilon e^{i\theta}}}{\epsilon e^{i\theta}((\epsilon e^{i\theta})^2+a^2)}i\epsilon e^{i\theta}d\theta = \int_{\pi}^0 \frac{ie^{im\epsilon e^{i\theta}}}{\epsilon^2e^{2i\theta}+a^2} d\theta,$$
so by taking the limit as $\epsilon$ approaches zero, you get
$$\lim_{\epsilon \to 0} \int_{\gamma}f(z)dz = \int_{\pi}^0\frac{i}{a^2}d\theta = -\frac{\pi i}{a^2}. \tag{4}$$
Then, by letting $R\to\infty$ and $\epsilon\to 0$ in (1), you can insert (2)-(4) into (1). This yields
$$-\frac{\pi i}{a^2e^{ma}} = -\frac{\pi i}{a^2} + \int_{-\infty}^{0}f(z)dz + \int_{0}^{\infty}f(z)dz = -\frac{\pi i}{a^2} + \int_{-\infty}^{\infty}f(z)dz,$$
or
$$\int_{-\infty}^{\infty}f(z)dz = \int_{-\infty}^{\infty}\frac{e^{imz}}{z(z^2+a^2)}dz = \frac{\pi i}{a^2} - \frac{\pi i}{a^2e^{ma}} = \frac{\pi i}{a^2}\left(1-\frac{1}{e^{ma}}\right). \tag{5}$$
Now, switching back to the real variable $x$ and also taking the imaginary part of (5), you get
$$\int_{-\infty}^{\infty}\frac{\sin(mx)}{x(x^2+a^2)}dx = \frac{\pi}{a^2}\left(1-\frac{1}{e^{ma}}\right). \tag{6}$$
And lastly, because the integrand of (6) is even,
$$\int_{0}^{\infty}\frac{\sin(mx)}{x(x^2+a^2)}dx = \frac{\pi}{2a^2}\left(1-\frac{1}{e^{ma}}\right)\tag{7},$$
which was to be shown.
