41

If I have two variables $X$ and $Y$ which randomly take on values uniformly from the range $[a,b]$ (all values equally probable), what is the expected value for $\max(X,Y)$?

Did
  • 279,727
John Smith
  • 837
  • The answers all assume that $X$ and $Y$ are independent. Without this assumption the question cannot be answered. If you meant to imply this assumption, please add it to the question. – joriki Jan 11 '20 at 09:24
  • https://math.stackexchange.com/q/1874340/321264 – StubbornAtom May 19 '20 at 15:12

5 Answers5

56

Here are some useful tools:

  1. For every nonnegative random variable $Z$, $$\mathrm E(Z)=\int_0^{+\infty}\mathrm P(Z\geqslant z)\,\mathrm dz=\int_0^{+\infty}(1-\mathrm P(Z\leqslant z))\,\mathrm dz.$$
  2. As soon as $X$ and $Y$ are independent, $$\mathrm P(\max(X,Y)\leqslant z)=\mathrm P(X\leqslant z)\,\mathrm P(Y\leqslant z).$$
  3. If $U$ is uniform on $(0,1)$, then $a+(b-a)U$ is uniform on $(a,b)$.

If $(a,b)=(0,1)$, items 1. and 2. together yield $$\mathrm E(\max(X,Y))=\int_0^1(1-z^2)\,\mathrm dz=\frac23.$$ Then item 3. yields the general case, that is, $$\mathrm E(\max(X,Y))=a+\frac23(b-a)=\frac13(2b+a).$$

Did
  • 279,727
  • 1
    Hi, would you please tell me what theorem step 2 comes from? – Austin Jan 26 '16 at 01:24
  • 2
    @Larry Theorem? Rather, the observation that ${\max(X,Y)\leqslant z}={X\leqslant z,Y\leqslant z}$, plus independence. – Did Jan 26 '16 at 01:57
  • 1
    I feel really dumb for asking this, but why is this true? I can't remember my professor ever mentioning the min or max functions in my previous probability course. – Austin Jan 26 '16 at 02:22
  • 1
    @Larry ?? $\max(x,y)\leqslant z\iff (x\leqslant z \land y\leqslant z)$. Not a probabilistic result... – Did Jan 26 '16 at 08:19
  • This is totally true...You can think $Z= \max{(x,y)}$ – Xiaonan Aug 08 '16 at 06:18
  • What can be done if independence of $X$ and $Y$ is not satisfied? – Galen Dec 07 '21 at 04:00
20

I very much liked Martin's approach but there's an error with his integration. The key is on line three. The intution here should be that when y is the maximum, then x can vary from 0 to y whereas y can be anything and vice-versa for when x is the maximum. So the order of integration should be flipped:

enter image description here

jscg
  • 301
11

did's excellent answer proves the result. The picture here 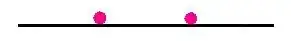enter image description here

may help your intuition. This is the "average" configuration of two random points on a interval and, as you see, the maximum value is two-thirds of the way from the left endpoint.

  • 9
    -1 Sorry for the down vote. I know what you mean, but I hate such examples, as it confuses the situation for those who do not fully understand what an "average" configuration means. – Calvin Lin Jul 01 '13 at 02:57
  • 12
    I don't follow. In what sense is this an average configuration? – Jonah Jul 09 '13 at 18:02
1

Since x and y are independent random variables, we can represent them in x-y plane bounded by x=0, y=0, x=1 and y=1. Also we can say that choosing any point within the bounded region is equally likely. So, if were to choose a small area around a set of value (x,y)- probability of that, i.e., ***P(X=x,Y=y)= dx.dy/(A)***. Where A is the total area where (x,y) might belong, Hence A=1*1= 1. Also note that $$\iint_{A} P(X=x,Y=y)=\iint_{A}\frac{(dx)(dy)}{1}= 1$$ Hence, P(X=x,Y=y) is indeed a probability density function. Please see the Image of random variables in xy plane.

Now, let Z= max(x,y). Note that when (x,y) is below the line y=x (i.e, x>y); Z=x When (x,y) is above the line y=x (i.e, y>x), Z=y. So if we compute the expected value over the whole region it would be; $$\iint_{A} Z \times P(X=x,Y=y)=\int_{0}^1\int_{0}^x x\frac{dydx}{1}+\int_{0}^1\int_{x}^1 y\frac{dydx}{1}=\int_{0}^1 x^2dx+\int_{0}^1 \frac{1}{2}\times(1-x^2)dx= \frac{2}{3} $$

aishik roy chaudhury
  • 125
1

I find the approach described in https://www.probabilitycourse.com/chapter4/4_1_3_functions_continuous_var.php easy to follow and applicable for this problem. It's a 3 step process

  1. Get the range of the required distribution, in this case, max(X, Y)
  2. Find the CDF of this distribution as a function of the known distributions
  3. Find the PDF of the distribution by differentiating the CDF

Let's say our new distribution is denoted by Z, it takes values in the range [0,1]

$P(Z <= z) = P(Max(X, Y) <= z)$

= $P((X,Y) <= z)$

= $P(X <= z,Y <= z)$

= $P(X <= z) . P(Y <= z)$

= $(z-a) \over (b-a) $ . $(z-a) \over (b-a) $

It can be used to get the CDF for [0,1] uniform distribution, PDF is differential of the CDF and E[Z] will be straightforward integral over [0,1].

PS: There is another approach described in the book for generic order static problems but the proof is relatively involved when compared to this approach.

svanga
  • 11