What is the expected number of times a dice has to be rolled to get two consecutive sixes?

Question

Basically, on average, how many times one should roll to expect two consecutive sixes?

Answer 1

Instead of finding the probability distribution, and then the expectation, we can work directly with expectations. That is often a useful strategy.

Let $a$ be the expected additional waiting time if we have not just tossed a $6$. At the beginning, we certainly have not just tossed a $6$, so $a$ is the required expectation. Let $b$ be the expected additional waiting time if we have just tossed a $6$.

If we have not just tossed a $6$, then with probability $\frac{5}{6}$ we toss a non-$6$ (cost: $1$ toss) and our expected additional waiting time is still $a$. With probability $\frac{1}{6}$ we toss a $6$ (cost: $1$ toss) and our expected additional waiting time is $b$. Thus $$a=1+\frac{5}{6}a+\frac{1}{6}b.$$ If we have just tossed a $6$, then with probability $\frac{5}{6}$ we toss a non-$6$, and then our expected additional waiting time is $a$. (With probability $\frac{1}{6}$ the game is over.) Thus $$b=1+\frac{5}{6}a.$$ We have two linear equations in two unknowns. Solve for $a$. We get $a=42$.

Answer 2

The formula is proved in the link given by Byron. I'll just try to give you my intuition regarding the formula.

The chance of rolling 6 on two dice is $1/36$. So if you think of rolling two dice at once as one trial, it would take an average of $36$ trials.

However, in this case you are rolling 1 die at a time, and you look at two consecutive rolls. The average number of trials to see the first 6 is $6$ times. Suppose we roll one more times to see if the two 6's are consecutive. Record the sequence of all rolls as

$$???????6?$$

where $?$ stands for any number that is not 6. The length of this sequence is random, but the average length of this sequence is $7$.

Now, the question is how many sequences of this type we will see before we get a sequence that ends in $66$. Since we are only interested in the last number of the sequence, there is a $1/6$ chance that the sequence will end in $66$. The same argument says that the average number of sequences we will need is $6$. Multiply this with the average length of the sequence to get $7 \cdot 6 = 42$ as the answer.

This argument generalizes to more than $2$ consecutive 6's by induction. For example, if you want $3$ consecutive 6's, you consider sequences that look like this:

$$ ???????66? $$

The average length of a sequence of this type is $42 + 1 = 43$. Therefore, the answer is $43 \cdot 6 = 258$.

It's not hard to generalize this situation. The general form is $L_{n+1} = \frac{1}{p}(L_n + 1)$ where $p$ is the probability of the desired symbol appearing and $L_n$ is the average number of trials until the first occurrence of $n$ consecutive desired symbols. (By definition, $L_0 = 0$.) This recurrence can be solved pretty easily, giving the same formula as in Byron's link. (The proof is essentially the same too, but my version is informal.)

Answer 3

Here is a generating function approach to this question. Consider the following atomic rolls:

$\mathbf{a}$. $1$-$5$ ($5/6$ chance, $1$ roll) represented by $\frac56x$

$\mathbf{b}$. $6$ followed by a $1$-$5$ ($5/36$ chance, $2$ rolls) represented by $\frac5{36}x^2$

$\mathbf{c}$. $6$ followed by a $6$ ($1/36$ chance, $2$ rolls) represented by $\frac1{36}x^2$

Each possible scenario ending in a double $6$ is captured exactly once by a certain number of $\mathbf{a}$ or $\mathbf{b}$ atoms followed by a $\mathbf{c}$ atom. The monomial representations have a coefficient equal to the probability of that atomic roll and an exponent of $x$ equal to the number of rolls.

Note that the coefficient of $x^n$ in $\left(\frac56x+\frac5{36}x^2\right)^k\frac1{36}x^2$ is the probability of ending in $n$ rolls having rolled $k$ $\mathbf{a}$ or $\mathbf{b}$ atoms followed by $1$ $\mathbf{c}$ atom. Summing these up for all $k$ yields a formal power series in which the coefficient of $x^n$ is the probability of ending in exactly $n$ rolls.

That is, the generating function for the probability of ending in exactly $n$ rolls is $$ f(x)=\frac{\frac1{36}x^2}{1-\frac56x-\frac5{36}x^2}\tag{1} $$ As a check, notice that $f(1)=1$, so the sum of the probabilities is $1$.

Now to find $\mathrm{E}(n)$, the expected value of $n$, we take a derivative, multiply by $x$, and evaluate at $1$: $$ xf'(x)=\frac{\frac1{36}x^2\left(2-\frac56x\right)}{\left(1-\frac56x-\frac5{36}x^2\right)^2}\tag{2} $$ Evaluating $(2)$ at $x=1$ yields $\mathrm{E}(n)=42$.

Next, to find $\mathrm{E}(n^2)$, we take another derivative, multiply by $x$, and evaluate at $1$: $$ xf'(x)+x^2f''(x)=\frac{\frac1{36}x^2\left(4-\frac52x+\frac54x^2-\frac{25}{216}x^3\right)}{\left(1-\frac56x-\frac5{36}x^2\right)^3}\tag{3} $$ Evaluating $(3)$ at $x=1$ yields $\mathrm{E}(n^2)=3414$. Thus, the variance of the number of rolls is $\mathrm{E}(n^2)-\mathrm{E}(n)^2=3414-42^2=1650$.

Therefore, the expected number of rolls is $42$ with a standard deviation of $\sqrt{1650}\approx40.62$.

Distribution: Here is a plot of the probabilities of getting a double $6$ on a particular roll. I was surprised that the probability for both $3$ and $4$ rolls was $\frac5{216}$.

$\hspace{2cm}$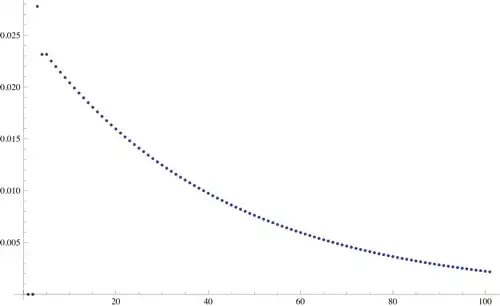

Extension: I have added a generating function answer to the more general question that Byron references in his answer.

Answer 4

Plugging $n=2$ and $p=1/6$ into my answer here, we see that the answer is $6^2+6=42$.

Answer 5

Adding up to Andre's answer. The framework proposed in the solution can be generalized to obtain a formula of expected time as of $t = 0$ for $n$ consecutive throws of any number in the dice as follows. Let $a_1$ = expected additional waiting time if we have not just tossed the number of interest (say, six), $a_{n}$ = expected additional waiting time given we have tossed $n-1$ sixes at $t = n-1$. Then based on Andre's framework, we can solve the following system of equations recursively to obtain a formula of the expected time to obtain $n$ consecutive throws of any number in the dice:

$$a_1 = 1 + \frac{5}{6}a_1 + \frac{1}{6}a_2$$ $$a_2 = 1 + \frac{5}{6}a_1 + \frac{1}{6}a_3$$ $$...$$ $$a_{n-1} = 1 + \frac{5}{6}a_1 + \frac{1}{6}a_n$$ $$a_{n} = 1 + \frac{5}{6}a_1$$

Solving recursively, we can obtain an function for the expected waiting time in terms of the number of consecutive throws we would like to observe:

$$a_1 = \sum^{n-1}_{i=0} (\frac{1}{6})^i +\frac{5}{6}a_1 \sum^{n-1}_{i=0} (\frac{1}{6})^i + (\frac{1}{6})^na_n$$

Using the properties of geometric series and substituting $a_n$, we obtain the following expression for $a_1$

$$a_1 = (6^{n+1} - 6)\frac{6}{5} + 6$$

The result indicated by Andre is obtained when we set $n = 1$, i.e. the expected waiting time for one consecutive throw. Additionally, we see that for zero consecutive throws, we are expected to throw 6 times to obtain a six, which is in line with what we know about fair dices.

Answer 6

Another method is to approach this with Linear Algebra and the use of Absorbing Markov Chains and Stochastic Matrices.

We describe the scenario as a markov chain with the states $A_2,A_1,A_0$ corresponding to two, one, or zero sixes most recently seen. We have the following transition matrix:

$$\begin{bmatrix}1& \frac{1}{6}&0 \\0 &0&\frac{1}{6} \\0& \frac{5}{6}& \frac{5}{6}\end{bmatrix}$$

This is in the standard format of $\left[\begin{array}{c|c}I&S\\\hline 0&R\end{array}\right]$

The fundamental matrix, $(I-R)^{-1}$ contains a great deal of useful information, including in this case, the expected number of turns it will take to reach an absorbing state (which in this case corresponds to getting two sixes in a row).

$(I-R)^{-1}=\left(\begin{bmatrix}1&0\\0&1\end{bmatrix}-\begin{bmatrix}0&\frac{1}{6}\\\frac{5}{6}&\frac{5}{6}\end{bmatrix}\right)^{-1}=\begin{bmatrix}1&-\frac{1}{6}\\-\frac{5}{6}&\frac{1}{6}\end{bmatrix}^{-1}$

$$=\begin{bmatrix}6&6\\30&36\end{bmatrix}$$

As when we begin the markov process, we start in state $A_0$ with no currently seen sixes, we look to the corresponding column in our fundamental matrix, the way I've written it will be the second column. Adding the entries of said column will tell us the expected time until we reach an absorbing state. That is to say, the expected number of throws of the die until you get two sixes in a row is:

$$6+36=42$$

Answer 7

Use the following generating function with $z$ representing sixes and $w$ the remaining values:

$$z + (1+z)\sum_{q\ge 1} \left(\frac{w}{1-w} z\right)^q.$$

As the remaining values other than six contribute to the number of rolls we now work with

$$f(z) = z + (1+z)\sum_{q\ge 1} \left(\frac{wz}{1-wz} z\right)^q \\ = z + (1+z) \frac{wz^2/(1-wz)}{1-wz^2/(1-wz)} \\ = z + (1+z) \frac{wz^2}{1-wz-wz^2}.$$

The quantity we seek is (we start at one because the GF has no constant term and the first admissible case is for $n=1$)

$$\sum_{n\ge 1} 6^{-(n+1)} (n+1) [z^n] \left.\left(z + (1+z) \frac{wz^2}{1-wz-wz^2}\right)\right|_{w=5} \\ = \sum_{n\ge 1} \left(\frac{1}{6}\right)^{n+1} (n+1) [z^n] \left(z + (1+z) \frac{5z^2}{1-5z-5z^2}\right) \\ = \sum_{n\ge 1} \left(\frac{1}{6}\right)^{n+1} n [z^n] \left(z + (1+z) \frac{5z^2}{1-5z-5z^2}\right) \\ + \sum_{n\ge 1} \left(\frac{1}{6}\right)^{n+1} [z^n] \left(z + (1+z) \frac{5z^2}{1-5z-5z^2}\right).$$

There are two pieces here, the easy piece is

$$\frac{1}{6} \left(\frac{1}{6} + \frac{7}{6} \frac{5/36}{1-5/6-5/36}\right) = \frac{1}{6} \left(\frac{1}{6} + \frac{7}{6} \frac{5}{36-30-5}\right) \\ = 1.$$

This is as it ought to be because we are summing the probabilities of the event first two consecutive sixes happening after $n+1$ rolls of the dice.

The tricky piece is

$$\frac{1}{36} \sum_{n\ge 1} \left(\frac{1}{6}\right)^{n-1} n [z^n] \left(z + (1+z) \frac{5z^2}{1-5z-5z^2}\right) \\ = \frac{1}{36} \left.\left(z + (1+z) \frac{5z^2}{1-5z-5z^2}\right)' \right|_{z=1/6} \\ = \frac{1}{36} \left.\left(1 + \frac{5z^2}{1-5z-5z^2} + (1+z) \frac{10z}{1-5z-5z^2} \\ + (1+z) \frac{5z^2}{(1-5z-5z^2)^2} (5+10z) \right) \right|_{z=1/6} \\ = \frac{1}{36} \left(1 + 5/36/(1/36) + \frac{7}{6} 10/6/(1/36) + \frac{7}{6} 5/36/(1/36^2) \times (5+10/6)\right) \\ = \frac{1}{36} ( 1 + 5 + 70 + 7\times 5\times 40) = 41.$$

Collecting the two contributions we obtain

$$\bbox[5px,border:2px solid #00A000]{ 1+41 = 42.}$$