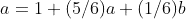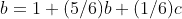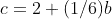0

I am asking this question because I don't know what is wrong with my method and for someone to explain where I went wrong. However, other methods are welcome as long as they don't use calculus(I'm in precalculus.)

I got this idea from André Nicholas's answer and Brilliant. I tried to use his method, however I didn't get the answer. Brilliant's solution just confused me.

My solution:

Let a be the expected number of rolls if the previous roll was not a 6. Let b be the expected number of rolls if the previous roll was a 6. Let c be the expected number of rolls if the previous 2 rolls were 6. Therefore:

enter image description here

enter image description here

enter image description here

The reasoning for this is that each roll has a probability of either not getting a six or getting one. c adds 2 because there were 2 rolls before it. If anyone needs clarification on what I mean please comment.

The correct answer is 258, but I got 54. I'm confused why my solution doesn't work.

Sidenote- From this post, I found out that for numbers on a die less than 6, the answer is 43(258/6). I'm unsure why it's 43 instead of 258. This isn't part of my question, however, if somebody could please explain it to me in the comments that would be great.

aSquaredRush
  • 21
  • 3
    $c=1+\left(\frac 56\right)a$. – lulu Jul 26 '20 at 00:20
  • 1
    @AarushChaubey the solution on brilliant is the same as yours, maybe a bit more general case. – Alexey Burdin Jul 26 '20 at 00:38
  • Why is it 1? I meant for c to be the last 6. It had 2 rolls before it. – aSquaredRush Jul 26 '20 at 00:39
  • @Alexey Burdin Yes, but they got the right answer. Plus, I just couldn't understand it. So, I tried to make my own equations. – aSquaredRush Jul 26 '20 at 00:41
  • 1
    If no last $6$ you got back to $a$, starting with $0$ consecutive $6$s -- with a probability of $\frac 56$. Btw, which part of the brilliant's solution is unclear? – Alexey Burdin Jul 26 '20 at 00:53
  • @AlexeyBurdin I was confused on why they used x_(n-1) in their solution. They said that you need n-1 6's to get n 6's which makes perfect sense. That is why I defined "a" as the number of previous rolls. However, what I got stuck on was if their solution was the same as mine. After reading it more thoroughly though, I realized it's the same. x_n-1 is the same as "a,b,c," and in "angryavian's"(can't notify more than one person) equation we added 1 to "a,b,c" just like in the Brilliant solution. – aSquaredRush Jul 26 '20 at 12:33

1 Answers1

1
  • Note that $b$ should be "expected rolls needed if the previous two rolls were "not 6, then 6." Otherwise there is overlap between "previous roll is 6" and "previous two rolls were both 6"
  • Expanding on lulu's correction: the "$+1$" in each equation is counting the current roll, not the previous ones. For instance, the logic for the first equation is really "if the current roll is not a six, then the expected remaining rolls needed is $a$; otherwise the expected remaining rolls needed is $b$, so it is $a = \frac{5}{6}(1 + a) + \frac{1}{6}(1+b) = 1 + \frac{5}{6} a + \frac{1}{6} b$. For the last equation, if the current roll is not a six, then you are back to "$a$," otherwise you are done and you just need to count the current roll, so it is $\frac{5}{6}(1+a) + \frac{1}{6} \cdot 1 = 1 + \frac{5}{6} a$.
angryavian
  • 89,882
  • 1
    Now it shows $a=258$, were we looking for $c=258$ instead? Where am I wrong?) – Alexey Burdin Jul 26 '20 at 01:19
  • @AlexeyBurdin We were looking for a=258. This post really helps, but I'll have to look at it more in depth in the morning. – aSquaredRush Jul 26 '20 at 03:36
  • @angryavian Thank you for your post it really helps, and I got the right answer. However, do you know why the post I left in my side note got 43? – aSquaredRush Jul 26 '20 at 12:20
  • @AarushChaubey In the other question, they are asking for how long it takes to get a triple of any number (not necessarily 6 or a predetermined one). It is much easier to get a triple of some number than it is to get a triple of a given number (like 6), so it takes far fewer rolls on average. (It is nice that it ends up working out to being exactly $1/6$ as many on average.) – angryavian Jul 26 '20 at 19:18
  • @angryavian What's the difference between any number and a given number? – aSquaredRush Jul 26 '20 at 20:37
  • @AarushChaubey In the other problem, you stop if you get "1, 1, 1" or "4, 4, 4," but in your problem you would have to keep rolling until you get "6, 6, 6." – angryavian Jul 26 '20 at 20:39
  • Ohhhhhh. That makes complete sense thank you. – aSquaredRush Jul 27 '20 at 18:29