What are the restrictions on using substitution in integration?
For example, integration in this case may be done by the substitution $u=\tan x$, as seen in the following $\textit{Mathematica}$ notebook
Integration done by substitution $u=\tan {x\over 2}$.

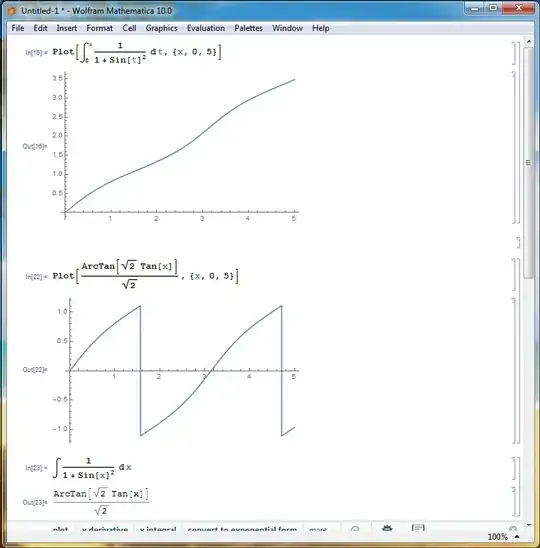
The source function is a continuous positive function over $\mathbb {R}$ which implied by necessity that its antiderivative is continuous and increasing over $\mathbb {R}$ (which contradicts the graph of its analytical antiderivative that has jumb discontinuities).
When I sent this question to Dr.Math, he replied - thanks to him - that the antiderivative of the function $ f(x)={1\over {1+{\sin x}^2}} $ is:
$$ {\tan^{-1} (\sqrt 2 \tan x) \over \sqrt 2} + \lfloor \frac x \pi-\frac 12 \rfloor * \frac{\pi}{\sqrt 2} + C $$
Which matches the "True" antiderivative of the function after redefining the integral at $( {\pi \over 2} + n.\pi) $. The second term has a derivative of $0$ over $ \Bbb R $.
This kind of "weird" functions makes me wonder about the "Restrictions" on using substitution when evaluating integrals, how to know that the function I work on needs refinements, and how to construct this "True" antiderivative ?