According to this site,
$$ \int \frac{1}{a^2 \cos^2(x) + b^2 \sin^2(x)} \,dx =\frac{1}{ab} \arctan\left(\frac{b}{a} \tan(x)\right)$$
Thus, $$ \int_0^{\pi} \frac{1}{a^2 \cos^2(x) + b^2 \sin^2(x)} \, dx =\frac{1}{ab} \arctan\left(\frac{b}{a} \tan(\pi)\right)-\frac{1}{ab} \arctan\left(\frac{b}{a} \tan(0)\right)=0-0=0$$
But in fact value of integral is not zero.
What am I doing wrong?
First, let us assume that $a, b > 0$ without loss of generality. Then in this regime, $f(x) = (a^2 \cos^2 x + b^2 \sin^2 x)^{-1}$ is clearly a well-defined function everywhere, and is periodic with period $\pi$. However, the antiderivative is not unique, and the particular choice of antiderivative $$F(x) = \frac{1}{ab} \tan^{-1} \left( \frac{b}{a} \tan x \right)$$ may not be continuous over a given interval. For example, if we choose the branch of $\tan^{-1}$ that restricts the range to lie in $(-\pi/2, \pi/2)$, then you get this picture for $a = 2$, $b = 0.5$:
As you can see, there is a jump discontinuity in the antiderivative at $x = \pi/2$ that could be rectified by choosing a different branch of the inverse tangent; e.g., we could choose $\tan^{-1}$ to have the range $[0,\pi)$. This fixes the discontinuity at $\pi/2$ so that a definite integral containing this point will not result in an incorrect evaluation.
In general, it is important when dealing with branches of multivalued functions to choose the branch appropriate to the interval or domain of integration, so as to avoid these problems.
An example of how you could specify an antiderivative that is continuous for all real $x$ provided that we state that the range of $\tan^{-1}$ is $(-\pi/2,\pi/2)$, is by writing it as $$F(x) = \begin{cases} \displaystyle \frac{1}{ab} \left( \tan^{-1} \left(\frac{b}{a} \tan x \right) + \pi \left(\lfloor 2x/\pi \rfloor - \lfloor x/\pi \rfloor\right) \right), & 2x/\pi \not \in \{\pm 1, \pm 3, \ldots\} \\ \displaystyle \frac{x}{ab}, & 2x/\pi \in \{\pm 1, \pm 3, \ldots\}. \end{cases}$$ But I think this is a rather complicated way to express the antiderivative. Instead, it might be better to state that the branch of the inverse tangent that is chosen depends on the argument of $x$; i.e., if we define $y = \tan^{-1} c \tan x$ for some $0 < c < \infty$, then $y$ is chosen such that $x, y \in ((2m-1)\pi/2, (2m+1)\pi/2)$ for a suitable integer $m$.
Note that, in the link, $u=\tan x$ which is increasing in $[0,\pi/2)$. In this integral, $x\in[0,\pi]$ and hence you can't use the result directly. In fact
$$ \int_0^\pi \frac{1}{a^2 \cos^2(x) + b^2 \sin^2(x)} \,dx=2\int_0^{\pi/2} \frac{1}{a^2 \cos^2(x) + b^2 \sin^2(x)} \,dx.$$ Use the result in $[0,\pi/2]$ and you will get the result.
Some Background on Integration by Substitution
It is important to understand the assumptions one makes in Integration by Substitution.
Let $I$ denote the integral given by $I=\int_a^b f(x)\,dx$.
Condition $(i)$: We assume that $f$ is continuous on $[a,b]$.
Condition $(ii)$: The inverse function $u^{-1}$, of $u(x)$ is continuously differentiable on $[u(a),u(b)]$.
Under Conditions $1$ and $2$, we have
$$\begin{align}I=&\int_a^b f(x)\,dx\\\\&=\int_{u(a)}^{u(b)}f(u^{-1}(t))\frac{du^{-1}(t)}{dt}\,dt \tag 1\end{align}$$
Note that the relationship expressed in $(1)$ can be obtained formally through the substitution $u(x)=t$, under Assumptions $(i)$ and $(ii)$.
Application to Evaluating $\int_0^\pi \frac{1}{a^2\sin^2(x)+b^2\cos^2(x)}\,dx$
To apply the substitution in $(1)$ correctly to evaluate the integral of interest, one must ensure that both $(i)$ and $(ii)$ are satisfied.
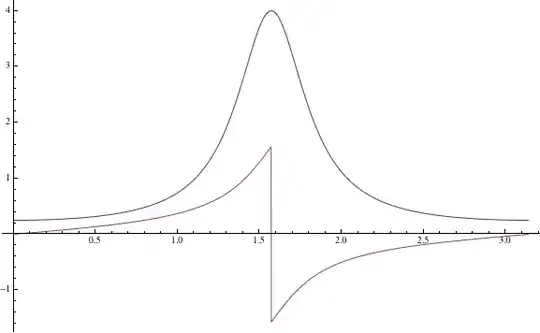
Since $f(x)=\frac{1}{a^2\sin^2(x)+b^2\cos^2(x)}$ is continuous for $x\in [a,b]$ and Condition $1$ is satisfied.
The substitution used in the reference cited in the OP is $\tan(x)=t$. Note that for $x\in [0,\pi]$ the inverse function for the tangent function is given by
$$\tan^{-1}(t)=\begin{cases}\arctan(t)&, t>0\\\\\pi+\arctan(t)&,t<0 \tag 2\end{cases}$$
where the $-\pi/2 < \arctan(x)<\pi/2$ is the principal branch of the inverse tangent function. The inverse tangent is not even continuous at $0$ and we cannot apply, therefore, the substitution over the interval $x\in [0,\pi]$.
Instead, we can write the integral as the sum
$$\begin{align} \int_0^\pi f(x)\,dx&=\lim_{\epsilon \to 0^+}\left(\int_0^{\pi/2-\epsilon}f(x)\,dx+\int_{\pi/2+\epsilon}^\pi f(x)\,dx\right) \end{align}$$
where $f(x)=\frac{1}{a^2\sin^2(x)+b^2\cos^2(x)}$.
The inverse tangent function $\tan^{-1}(x)$ as expressed in $(2)$ is continuously differentiable on each separate interval $x>0$ and $x<0$ and so, Condition $2$ is satisfied on each separate interval.
Then, we can write
$$\begin{align}\lim_{\epsilon \to 0^+}\int_0^{\pi/2-\epsilon}f(x)\,dx&=\int_0^{\infty}f(\arctan(t))\frac{1}{1+t^2}\,dt\\\\ \lim_{\epsilon \to 0^+}\int_{\pi/2+\epsilon}^\pi f(x)\,dx&=\int_{-\infty}^0f(\pi+\arctan(t))\frac{1}{1+t^2}\,dt \tag 3 \end{align}$$
Since $f(x)$ is even and $\pi$-periodic, then the second equality in $(3)$ is identical to the first. Therefore, we have
$$\begin{align} \int_0^\pi f(x)\,dx&=2\int_0^\infty \frac{f(\arctan(t))}{1+t^2}\,dt\\\\ &=2\int_0^\infty \frac{1}{a^2t^2+b^2}\,dt\\\\ &=\left. \frac{2\arctan(at/b)}{ab}\right|_{0}^{\pi/2}\\\\ &=\frac{\pi}{ab} \end{align}$$
This very integral, with a little manipulation, is referenced in the Jeffrey paper so the nice form in that paper can be attained by observing that $\tan^{-1}(\tan x)$ has the same discontinuities as the original integral, so we may hope to cancel them out by setting $$\frac1{ab}\tan^{-1}\left(\frac{b}a\tan x\right)=\frac1{ab}\left\{x+\tan^{-1}\left(\frac{b}a\tan x\right)-\tan^{-1}(\tan x)\right\}$$ Now, $$\begin{align}\tan^{-1}\left(\frac{b}a\tan x\right)-\tan^{-1}(\tan x) & =\tan^{-1}\left(\frac{\frac{b}a\tan x-\tan x}{1+\frac{b}a\tan^2x}\right) \\ & =\tan^{-1}\left(\frac{(b-a)\sin2x}{(a+b)-(b-a)\cos2x}\right) \end{align}$$ after a little algebra, so $$\int\frac1{a^2\cos^2x+b^2\sin^2x}dx=\frac1{ab}\left\{x+\tan^{-1}\left(\frac{(b-a)\sin2x}{(a+b)-(b-a)\cos2x}\right)\right\}+C$$ removes all discontinuities and even checks by differentiation.
