What is the chance that a PDF with compact support is concave?

Question

Relevant questions and answers, in chronological order:

• When do equations represent the same curve?
• Find a smooth function with prescribed moments
• Does a sequence of moments determine the function?

All of the questions and answers are related to the Moment problem . The functions considered have compact support (hope this terminology is correct). More specifically, the above Q & A list is related to the Hausdorff moment problem ; without loss of generality, the bounded interval is taken as $[0,1]$ . As pointed out in the Wikipedia reference, the following integral sheds more light on properties of the moments. Let $f(x)$ be real, integrable and positive with area $\,m_0 = 1\,$ equal to one - in short: $f(x)$ resembles a Probability Density Function (PDF) - then: $$ \int_0^1 f(x) x^n (1-x)^k dx > 0 \quad \Longrightarrow \quad \left\{ \begin{array}{l} m_0 > 0 \; , \; m_1 > 0 \; , \; m_2 > 0 \\ m_0 > m_1 \; , \; m_2 > m_1 \\ m_0 - 2 m_1 + m_2 > 0 \end{array}\right. $$ Attention will be restricted to the first few moments : $m_1,m_2$ . If we put $\;x = m_1/m_0=m_1\;$ and $\;y = m_2/m_0=m_2\;$ then it follows that all $(x,y)$ values are within the $\color{silver}{silver}$ triangle with vertices $(0,0),(0,1/2),(1,1)$ , as shown in the picture at the bottom. $$ y > 0 \quad ; \quad y < x \quad ; \quad y > 2 x - 1 $$ Schwarz' inequality gives rise to a somewhat more restrictive condition: all $(x,y)$ values are within the $\color{gray}{gray}$ area between a parabola and a straight line: $$ y < x \quad ; \quad y > x^2 $$ This is as far as I have been able to go with general considerations about moments. But if someone knows better, I'm eager to learn about it.

Special theories

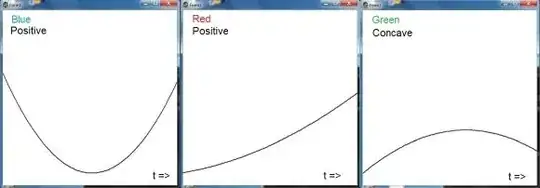
Couldn't proceed with the general, so I've tried some special cases. Because I think it's better to be successful with something special than to fail with anything general. This is the reason why I've payed so much attention to extremely simple PDF-functions, sample functions namely that are completely determined by their first few moments. Among these are:

• histograms consisting of three blocks with the same width

Please read the reference, because the argumentation shall not repeated here.

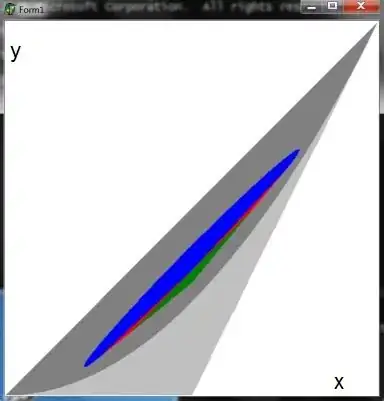
The three moments $\,m_0,m_1,m_2\,$ are linear in the three function values $f_0,f_1,f_2$ and vice versa. Meaning that there is a one-to-one mapping between function space and moment space $\,(x=m_1/m_0,y=m_2/m_0)\,$ where $m_0 = 1$ . The moment space of 3-histograms is in the picture below. If the only requirement is that the histogram is just positive (and with area $= 1$) then what we have is the $\color{blue}{blue\; triangle}$. If an additional requirement is that the histogram is concave then we have the $\color{green}{green\; triangle}$ as a proper part of the blue one. Let's formulate this as follows.
Consider the universe of all PDF 3-histograms, what then is the chance that such a histogram is concave ? The answer must be the quotient of the areas of the green and the blue triangle. With the above reference that is: $\,(4/243) / (1/27) = 4/9$ . With other words: $\large 4/9$ of all histograms in our special universe are concave.

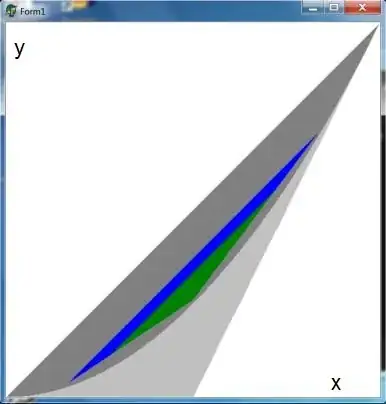
But this is indeed a very simple example. A couple of questions arise:

• In general, has an idea like this been launched before?
• If not in general, do there exist other special examples of PDF universes
  where the question "what is the chance that a PDF is concave" makes sense?

Answer 1

There is another example in the abovementioned special answer which is less complete there and shall be completed here.
Consider the universe of all PDF-like parabolic functions at the interval $t \in [0,1]$ : $$ p(t) = a_0 + a_1 t + a_2 t^2 $$ The following Q & A has been helpful with visualization of the parabolas:

• Maximum of parabolas at interval $[0,1]$

There is a linear relationship between the coefficients of the parabola and the first few moments, via the Hilbert matrix and its inverse: $$ \left[ \begin{array}{c} m_0 \\ m_1 \\ m_2 \end{array} \right] = \left[ \begin{array}{ccc} 1 & 1/2 & 1/3 \\ 1/2 & 1/3 & 1/4 \\ 1/3 & 1/4 & 1/5 \end{array} \right] \left[ \begin{array}{c} a_0 \\ a_1 \\ a_2 \end{array} \right] \quad \Longleftrightarrow \quad \left[ \begin{array}{c} a_0 \\ a_1 \\ a_2 \end{array} \right] = \left[ \begin{array}{ccc} 9 & -36 & 30 \\ -36 & 192 & -180 \\ 30 & -180 & 180 \end{array} \right] \left[ \begin{array}{c} m_0 \\ m_1 \\ m_2 \end{array} \right] $$ As usual, we define the coordinates in moment space as $\,x=m_1/m_0\,$ and $\,y=m_2/m_0\,$ with the area normed to one $\,m_0=1$ . Let's start with demanding that the parabolas are positive at $[0,1]$ . Which is e.g. the case if the discriminant is negative together with a positive leading coefficient: $$\color{blue}{ \left. \begin{array}{l} a_1^2 - 4 a_2 a_0 < 0 \\ a_2 > 0 \end{array} \right\} \quad \Longleftrightarrow \quad \left\{ \begin{array}{l} 152 x^2 - 300 x y + 150 y^2 - 42 x + 40 y + 3 < 0 \\ y - x + 1/6 > 0 \end{array} \right. } $$ Note that what's up here is exactly (the inside of) the ellipse that was questioned about in:

• Indefinite integral with sector of ellipse

with the line $y - x + 1/6 = 0$ tangent to it in $B=(1/2,1/3)$ .
This question and its answers are a prerequisite for understanding what follows.
Another way for the parabola to be positive is that $\;p(0) > 0\;$ and $\;p'(0) > 0\;$ , or $\;p(1) > 0\;$ and $\;p'(1) < 0\;$ , again with positive $a_2$ : $$ \color{red}{ \left. \begin{array}{l} a_0 > 0 \\ a_1 > 0 \\ a_2 > 0 \end{array} \right\} \quad \Longleftrightarrow \quad \left\{ \begin{array}{l} y - 6/5 x + 3/10 > 0 \\ y - 16/15 x + 1/5 < 0 \\ y - x + 1/6 > 0 \end{array} \right. } $$ $$ \color{red}{ \left. \begin{array}{l} a_0+a_1+a_2 > 0 \\ 2a_2+a_1 < 0 \\ a_2 > 0 \end{array} \right\} \quad \Longleftrightarrow \quad \left\{ \begin{array}{l} y - 4/5 x + 1/10 > 0 \\ y - 14/15 x + 2/15 < 0 \\ y - x + 1/6 > 0 \end{array} \right. } $$ At last we have the possibility that the parabola is concave and positive: $$ \color{green}{ \left. \begin{array}{l} a_0 > 0 \\ a_0+a_1+a_2 > 0 \\ a_2 < 0 \end{array} \right\} \quad \Longleftrightarrow \quad \left\{ \begin{array}{l} y - 6/5 x + 3/10 > 0 \\ y - 4/5 x + 1/10 > 0 \\ y - x + 1/6 < 0 \end{array} \right. } $$ Working out the data results in the "ellipse with a hat" geometry as has been presented before.
Now we are ready to answer the question: what is the probability that a parabolic PDF at $[0,1]$ is concave ? The answer is the area of the $\color{green}{green}$ triangle in the picture below divided by the area of the ellipse-with-a-hat as a whole (i.e. $\color{blue}{blue} + \color{red}{red} + \color{green}{green}$ ). And the end result is: $$ \frac{1/180}{\pi\sqrt{3}/180(1-1/3)+1/120+2/720+1/180} = \frac{1}{2\pi/\sqrt{3}+3} \approx 15 \% $$

If I am allowed to say something subjective: I find the geometry associated with this very specific problem of an astonishing beauty. It all fits so neatly together that it's almost a miracle.