$S(\mu,\sigma^2)$ has no extreme points. We can always write $f$ as an average of two variants, which we get by making adjustments at a few points.
To see this, find three adjacent triangles below the graph of $f$, e.g.:
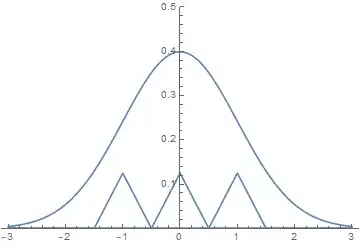
More formally, by the continuity of $f$, choose $b,u,v$ such that $f(x)>v>0$ for $x$ in $[b-3u,b+3u]$. Let
\begin{align}
f_1 &= v \max(0, 1-|x-b+2u|/u)\\
f_2 &= v \max(0, 1-|x-b+0u|/u)\\
f_3 &= v \max(0, 1-|x-b-2u|/u)\\
f_4 &= f-f_1-f_2-f_3\\
\end{align}
The picture above shows $f_1,f_2,f_3$ under a standard normal $f$, with $b=0,$ $u=1/2,$ $v=1/8.$
Now we seek functions in $S(\mu,\sigma^2)$ of the form $\sum w_i f_i$, so that the $w_i$ satisfy
$$\sum w_i\! \int\! f_i = 1,\ \ \sum w_i\! \int\! f_i x = \mu,\ \ \sum w_i\! \int\! f_i x^2 = \mu^2+\sigma^2.$$
When we integrate and put the $w_4$'s on the right hand side, this gives:
$$
\begin{pmatrix}
uv &uv(b-2u) &uv(b^2 - 4bu + \frac{25}{6} u^2)\\
uv &uv(b+0u) &uv(b^2 + 0bu + \frac{1}{6} u^2) \\
uv &uv(b+2u) &uv(b^2 + 4bu + \frac{25}{6} u^2)\\
\end{pmatrix}^T
\begin{pmatrix}
w_1 \\
w_2 \\
w_3 \\
\end{pmatrix}
=
\begin{pmatrix}
1 - (1-3uv)w_4 \\
\mu - (\mu-3buv)w_4\\
\mu^2 + \sigma^2 - kw_4 \\
\end{pmatrix}
$$
where $k=\mu^2+\sigma^2-uv(3b^2+\frac{51}{6}u^2).$
The matrix has determinant $16u^6v^3$, which is non-zero, so any value of $w_4$ yields a unique solution for $w_1,w_2,w_3$. When $w_4=1$, the solution is $w_1=w_2=w_3=1.$
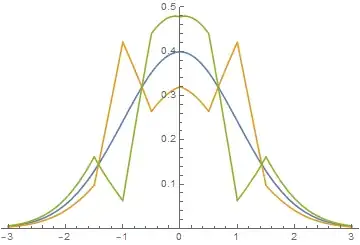
Now choose $\epsilon$ such that $w_4=1\pm\epsilon$ both yield positive values of $w_1, w_2, w_3$. Let $g$ be the value of $\sum w_i f_i$ corresponding to $w_4 = 1+\epsilon$, and let $h$ be the value corresponding to $w_4 = 1-\epsilon$. Then $f$ is an even mixture of $g$ and $h$.
In the example above, choosing $\epsilon=1/4$ gives $f,g,h$ as in the blue, green and orange of the graph below, and all are in $S(0,1)$.