1

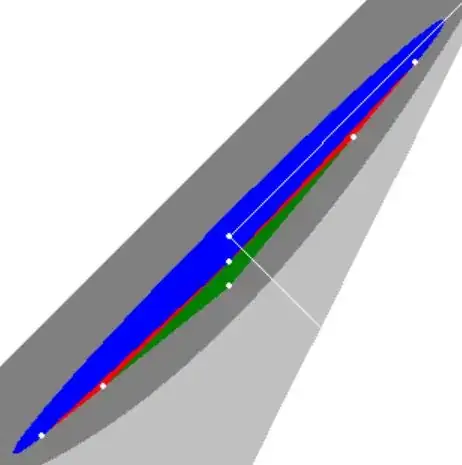
An ellipse is given by the following equation: $$ 152 x^2 - 300 x y + 150 y^2 - 42 x + 40 y + 3 = 0 $$ After solving for the midpoint we have: $$ 152 (x-1/2)^2 - 300 (x-1/2) (y-11/30) + 150 (y-11/30)^2 = 1/6 $$ Introducing polar coordinates: $$ x = 1/2 + r \cos(\theta) \quad ; \quad y = 11/30 + r \sin(\theta) $$ Giving: $$ 152\, r^2 \cos^2(\theta) - 300\, r^2\, \cos(\theta) \sin(\theta) + 150\, r^2 \sin^2(\theta) = 1/6 \quad \Longrightarrow \\ \frac{1}{2} r^2(\theta) = \frac{1/12} {152 \cos^2(\theta) - 300 \cos(\theta) \sin(\theta) + 150 \sin^2(\theta)} $$ The area of a sector of the ellipse is: $$ \int_{\theta_1}^{\theta_2} \frac{1}{2} r^2(\theta) \, d\theta $$ So it seems that we have to find the indefinite integral: $$ \int \frac{1/12 \, d\theta} {152 \cos^2(\theta) - 300 \cos(\theta) \sin(\theta) + 150 \sin^2(\theta)} $$ And then I'm stuck. Because feeding this into MAPLE with 

int(1/12/(152*cos(theta)^2-300*cos(theta)*sin(theta)+150*sin(theta)^2),theta);
quite to my surprise, gives a complex result: $$ {\frac {1}{720}}\,i\sqrt {3}\ln \left( \left( \tan \left( 1/2\,\theta \right) \right) ^{2}+ \left( {\frac {5}{38}}\,i\sqrt {3}+{\frac {75} {38}} \right) \tan \left( 1/2\,\theta \right) -1 \right) \\ -{\frac {1}{720 }}\,i\sqrt {3}\ln \left( \left( \tan \left( 1/2\,\theta \right) \right) ^{2}+ \left( -{\frac {5}{38}}\,i\sqrt {3}+{\frac {75}{38}} \right) \tan \left( 1/2\,\theta \right) -1 \right) $$ But I'm pretty sure that the area of an ellipse sector is a real number. So the question is: does there exist a closed form for the abovementioned integral that is real valued instead of complex? What is it? And why that complex result with MAPLE?

AfterMath (see accepted answer)
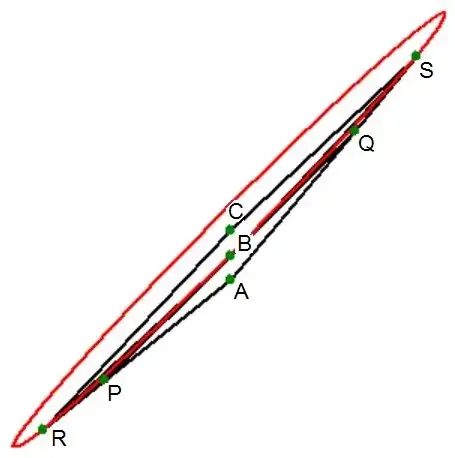
enter image description here

$$ A = (1/2,3/10) \quad ; \quad B = (1/2,1/3) \quad ; \quad C = (1/2,11/30) \\ P = (1/3,1/6) \quad ; \quad Q = (2/3,1/2) \\ R = (1/4,1/10) \quad ; \quad S = (3/4,3/5) $$ Triangle edges are black; ellipse is $\color{red}{red}$ .
Triangle areas: $\Delta PAQ = 1/180$ , $\Delta PRB = \Delta QSB = 1/720$ .
It is conjectured that the ellipse sector area $\overline{CRBSC}$ is exactly $1/3$ of the total ellipse area;
the latter being $ = \pi\sqrt{3}/180$ . Can someone prove or disprove this conjecture?

Han de Bruijn
  • 17,070
  • You have most of the necessary information for finding a linear (well, affine) mapping that takes the ellipse to, for example, the standard unit circle; your rays at angles $\theta_1$ and $\theta_2$ are mapped to two radii, area between explicit. Now map back, area is constant multiple. – Will Jagy Dec 01 '14 at 23:24
  • If you don't like that, any rational function of sine and cosine c an be transformed into a rational function using the Weierstrass substitution, http://en.wikipedia.org/wiki/Tangent_half-angle_substitution – Will Jagy Dec 01 '14 at 23:26

2 Answers2

2

$$\int\frac{dx}{a\cos^2x-b\cos x\sin x+c\sin^2x}=\frac2{\sqrt\Delta}\cdot\tanh^{-1}\bigg(\frac{b-2c\tan x}{\sqrt\Delta}\bigg)$$ where $\Delta=b^2-4ac$. If $\Delta<0$, just use Euler's formula to transform the hyperbolic arctangent of complex argument into a trigonometric one of real argument. For $\Delta=0\iff b=\pm2\sqrt{ac}$,

we get $I=\dfrac{b+(a+c)\sin2x}{(a+c)\Big[(a-c)+(a+c)\cos2x\Big]}$.

Lucian
  • 48,334
  • 2
  • 83
  • 154
  • In our case $b^2-4ac < 0$ because we have an ellipse. Does that mean that the outcome is:$$-\frac2{\sqrt\Delta}\cdot\tan^{-1}\bigg(\frac{b-2c\tan x}{\sqrt\Delta}\bigg)$$ with $\Delta = 4ac-b^2 > 0$ ? – Han de Bruijn Dec 02 '14 at 11:24
  • @HandeBruijn: Yes, exactly. $($ Mathematica agrees also $)$. – Lucian Dec 02 '14 at 12:10
  • Thanks, Lucian: I can calculate now the area of the desired sector. With the surprising result that it seems to be exactly $1/3$ of the total area of the ellipse ! Can't figure out why .. – Han de Bruijn Dec 02 '14 at 17:36
1

The integral is elementary. $$ I = \int \frac{d \theta} {a \cos^2(\theta) - b \cos(\theta) \sin(\theta) + c \sin^2(\theta)}= \int \frac{d \tan(\theta)} {a - b \tan(\theta) + c \tan^2(\theta)} $$ Let $u=\tan(\theta)$ , then: $$ I = \int \frac{d u}{c u^2 - b u + a} = \int \frac{d u/c}{\left[ u-b/(2c) \right]^2+a/c - \left[b/(2c)\right]^2}=\\ 2 \int \frac{d (2c u-b)}{(2c u-b)^2+(4ac-b^2)}= \frac{2}{\sqrt{4ac-b^2}} \int \frac{d\left[(2c u-b)/ \sqrt{4ac-b^2}\right]} {1+\left[(2c u-b)/\sqrt{4ac-b^2}\right]^2} $$ Now let $\Delta = \sqrt{4ac-b^2}$ and we're finished: $$ I(\;\tan(\theta)\;) = \frac{2}{\Delta} \arctan\left(\frac{2c\tan(\theta)-b}{\Delta}\right) $$ Fill in the numbers for our sector: $a = 152\;,\;b = 300\;,\;c = 150$ , $\tan(\theta_2) = 16/15\;,\;\tan(\theta_1) = 14/15$ ; remember that an $\arctan$ is only defined for arguments $\in \left[-\pi/2,+\pi/2\right]$ and that the whole area of the ellipse equals $\pi\sqrt{3}/180$ . Then: $$ \mbox{area} = \frac{\pi\sqrt{3}}{180}/2 - \left[\;I(16/15)-I(14/15)\;\right]/12 = \frac{\pi\sqrt{3}}{540} $$ Thus establishing that the AfterMath conjecture is true. So finally we have all the ingredients to calculate the area of the "ellipse with a hat" ( $\color{blue}{blue} + \color{red}{red} + \color{green}{green}$ ) : $$ \color{blue}{\pi\sqrt{3}/180(1-1/3)+1/120}+\color{red}{2/720}+\color{green}{1/180} = \frac{\pi\sqrt{3}}{270}+\frac{1}{60} $$ enter image description here

Han de Bruijn
  • 17,070