Euler triangle inequality proof without words

Question

Today I was studying geometric inequalities and I saw this inequality: $$R \ge 2r$$

Unfortunately, the book did not provide any proof or further explanations. So I just did a little research about it. I found that the name of inequality is euler triangle inequality and there was a simple proof about it.

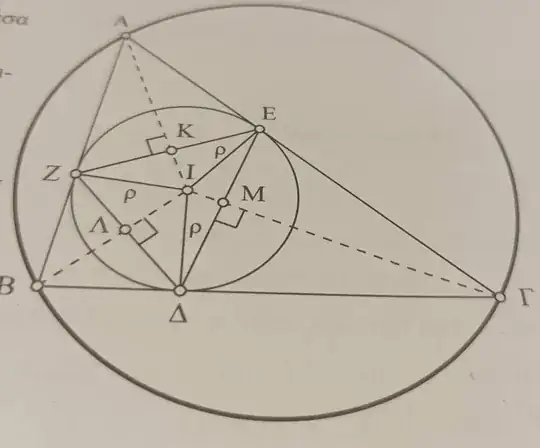
If $O$ is circumcenter of $\triangle ABC$ and $I$ is incenter of it and $OI=d$ then $$d^2=R(R-2r)$$ $R$ is circumradius and $r$ is inradius. from this identity we can drive $R-2r\ge0 \Rightarrow R\ge2r$

but I did not like this proof. So I continued my research till I found this from MAA.

First, the author proves 3rd lemma and using them simply proves the inequality. My problem was on understanding second lemma. Here is a description about it:

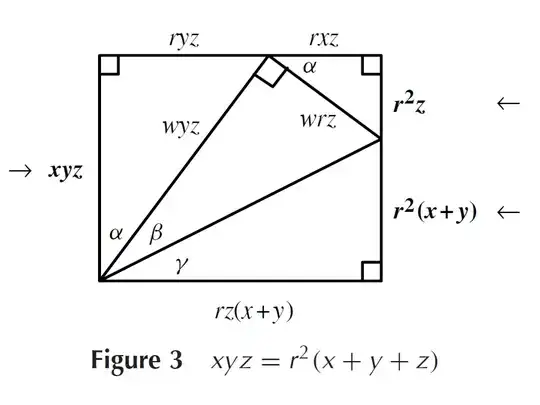
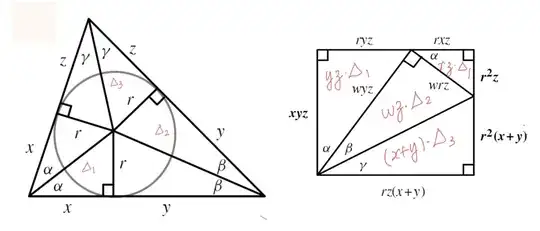
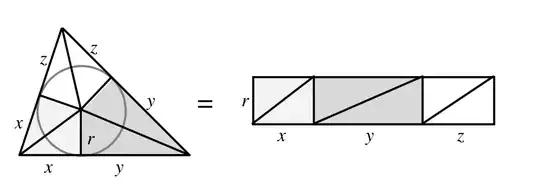
The second, whose proof uses a rectangle composed of triangles similar to the right triangles in FIGURE 1(b), expresses the product $xyz$ in terms of the inradius $r$ and the sum $x + y + z$.

Figure 1(b)

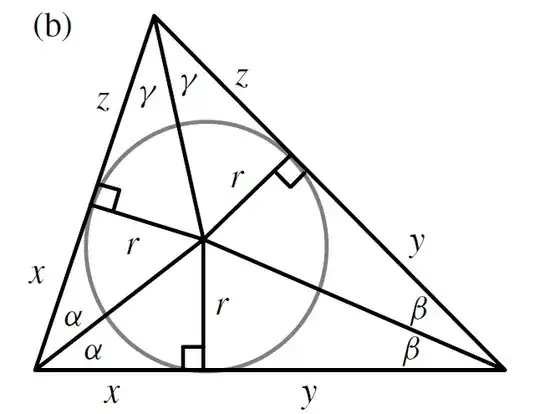
And the lemma proof

LEMMA 2. $xyz = r^2(x + y + z)$.

Proof. Letting $w$ denote $\sqrt{r^2+x^2}$, we have

I can't understand what sides are given in figure 3 and I can't reach $r^2(x+y)$ (I tried using Pythagorean but I was not succesful).

Answer 1

Proof of $R\geq2r$:

To prove that $R\geq2r$, we need 3 results:

result 1

$$\boxed{x y z =r^{2}(x+y+z)} $$ Denote the 3 pairs of congruent triangles by $\triangle_1, \triangle_2, \triangle_3.$

Enlarging $\triangle_1$ by factors $yz$ and $rz$ to create 2 more similar triangles; $\triangle_2$ by factor $wz$ to create 1 more similar triangle; $\triangle_3$ by factor $x+y$ to create 1 more similar triangle, and grouping these 4 new triangles to form a rectangle in which opposite sides are equal $$ x y z =r^{2} z+r^{2}(x+y)=r^{2}(x+y+z) $$

result 2

$$\boxed{4KR=abc}, $$ which is proved in my post

result 3

$$\boxed{K=r(x+y+z)}$$

By these 3 results, we can prove $R\geq2r$ now.

Using $A.M.\geq G.M.$, we have $$ 4 K R \stackrel{result 2}{=} a b c=(x+y)(y+z)(x+z) \geq 8 x yz $$

Hence $$ K R \geqslant 2 x y z \stackrel{result 1}{=} 2 r^{2}(x+y+z) \stackrel{result 3}{=} 2Kr $$

Now we can conclude that $$\boxed{R\geq 2r}.$$

Answer 2

The "$\alpha$" triangle on the left of Figure 3 is an "$\alpha$" triangle from Figure 1b, but scaled by $yz$; so, instead of side-lengths $r$, $x$, $w \;(=\sqrt{r^2+x^2})$, it has side-lengths $r\cdot yz$, $x \cdot yz$, $w \cdot yz$.

Likewise, the "$\alpha$" triangle in the upper-right of Figure 3 is scaled by $rz$ to have side-lengths $x\cdot rz$, $r \cdot rz$, $w\cdot rz$.

This gives the "$\beta$" triangle a scale factor of $wz$ (leg-lengths $y\cdot wz$ and $r\cdot wz$); and, from comparing the top of the rectangle to the bottom, we have that the "$\gamma$" triangle has scale factor $r(x+y)$ (leg-lengths $z\cdot r(x+y)$ and $r\cdot r(x+y)$).

Answer 3

We will show that $$OI^2=R^2-2Rr$$

Let inversion I with pole $I$ and ratio $k=r^2$, i.e. with circle of inversion the incircle of $ABC$. We have that $IZ^2=IK\cdot IA\Leftrightarrow IK\cdot IA=r^2$. so the inverse of A is Kwhich is the mean of $ZE$. Therefore, $I(A)=K, I(B)=L, I(C)=M$, so the inversion makes the incircle of $ABC$ the Euler's Cirlce of $DEZ$ . But Euler's Circle of $DEZ$ has $\frac{r}{2}$ and because the two circled are inverse this means that: $$\frac{\frac{r}{2}}{R}=\frac{k}{R^2-OI^2}$$, which finally gives that $$OI^2=R^2-2rR$$

The inequality you want to prove is a direct conclusion by the fact that $OI^2\geq0$