1

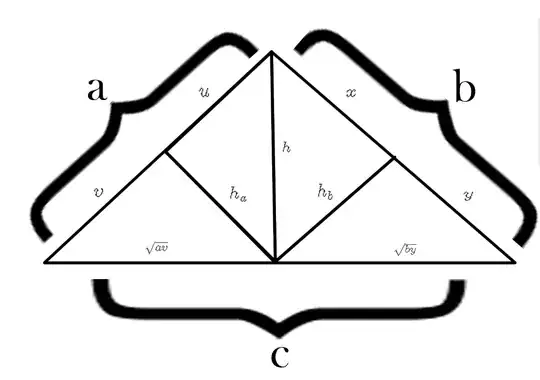
A triangle with side lengths $a, b, c$ an altitude($h$), where the height($h_a$) intercepts the hypotenuse($a$) such that it is the sum of two side lengths, $a = u +v$ and height($h_b$) intercepts hypotenuse($b$) such that it is also the sum of two side lengths $b = x + y$, we can find a simple proof of herons formula.

Image here:

(Note that $h = \sqrt{au}$ and $h = \sqrt{bx}$, giving $au = bx$)

First the equations we have are:

$u + v = a$

$x + y = b$

$au = bx$

$\sqrt{av} + \sqrt{by} = c$

Substituting $v$ and $y$ with $u$ and $x$ for the $4$th equation:

$\sqrt{a^2 - au} + \sqrt{b^2 - bx} = c$

Then using $au = bx$ we eliminate $x$ to find $u$:

$\sqrt{a^2-au}+\sqrt{b^2-b\left(\frac{au}{b}\right)}=c$

$u = \frac{1}{4ac^2}(2a^2b^2+2a^2c^2-a^4-b^4+2b^2c^2-c^4)$

Finally, substituting this into $h = \sqrt{au}$:

$h = \sqrt{\frac{1}{4c^2}(2a^2b^2+2a^2c^2-a^4-b^4+2b^2c^2-c^4)}$

Plugging this into the area formula ($A = \frac{1}{2}ch$) gives:

$A = \frac{1}{2}c\sqrt{ \frac{1}{4c^2}(2a^2b^2+2a^2c^2-a^4-b^4+2b^2c^2-c^4)} $

$A = \sqrt{\frac{1}{16}(c^2 - (a - b)^2)(( a + b)^2 - c^2)} $

$A = \sqrt{\frac{1}{16}(a + b - c)( a + b + c)( b + c - a)(a + c - b)} $

$A = \sqrt{s(s - a)(s- b)(s- c)}$

Q.E.D.

Thoughts?

SpoonedBread
  • 335
  • This looks similar to this answer. – robjohn Feb 23 '21 at 17:12
  • 1
    That's a proof that uses Pythagorean theorem directly, mine avoids direct use. – SpoonedBread Feb 23 '21 at 17:14
  • 1
    What is the exact question please..? – lone student Feb 23 '21 at 17:16
  • Is it an accurate\valid proof? – SpoonedBread Feb 23 '21 at 17:17
  • 2
    @SpoonedBread: You want to make sure that the foot of altitude $h$ lies within side $c$. (Otherwise, you need to accommodate the possibility that $c$ is not necessarily the sum of $\sqrt{av}$ and $\sqrt{by}$.) Assuming that $c$ is the longest side will guarantee this. (I feel like I've offered this advice before. :) – Blue Feb 23 '21 at 17:38
  • 3
    It looks valid, however, it essentially proves, along the way, the part of the Pythagorean Theorem used. That seems to encumber the proof rather than making it elegant, but that is a matter of opinion. – robjohn Feb 23 '21 at 17:43

2 Answers2

1

It is certainly a correct proof of Heron's formula that I have not seen before. I don't believe that it is any simpler than the other proofs that I have seen, but I am still entertained by it. However, I do not know if this is an appropriate posting since you do not really have a question other than possibly 'is my proof correct?'. I believe that the stack exchange guidelines suggest we only post questions and answers, not discussions.

Sohail Farhangi
  • 65
  • 7
1

In my post, I had shown that $$ r^{2}(x+y+z)=x y z \tag*{(result 1)} $$ and $$ K=r s \tag*{(result 3)} $$ where $s=x+y+z$ is the semi-perimeter of the triangle ABC whose area is $K$ and sides $a=y+z, b=z+x $ and $c=x+y$.

From (1), $r^{2} s=x y z$ implies that $$ K^{2}=r^2s^2 =sxy z=s(s-a)(s-b)(s-c) $$

Taking square root on both sides yields the Heron’s Formula $$ K=\sqrt{s(s-a)(s-b)(s-c)} $$

Lai
  • 20,421