Compute the inradius of a triangle and deduce Heron's formula

Question

In an exercise I am asked to compute the inradius and prove Heron's formula with the following steps:

1. $AD = AF = s - a$
2. $ AB+BE′=AD′=s$
3. $IDB$ y $BD′I′$ are similar

Here, $s$ is the semiperimeter.

This is a picture that shows the proof:

What I already proved was 1. (from similarity between triangles inside of $\triangle ABC$ constructed by inradius and bisectors) and 3. (by AAA similarity theorem) but I can't get some insight about 2.

• How can I prove 2.?
• When I prove these steps, how do they lead me to the inradius and Heron's formulas?

$\rho = \sqrt{\frac{(s-a)(s-b)(s-c)}{s}}$

$A = \rho s = \sqrt{s(s-a)(s-b)(s-c)}$

Answer 1

To prove (2), use that the segments from a point to two tangent points are equal. $BD'=BE'$, so $AB+BE'=AB+BD'=AD'$. Similarly, if $F'$ is the point where the excircle touches the extension of $AC$, $AC+CE'=AF'$. By the same property, $AF'=AD'$. However, $2AD'=AF'+AD'=AB+BE'+CE'+AC=P$ where $P$ is the perimeter of $\triangle ABC$.

To prove the formula, first use that $\triangle ADI\sim \triangle AD'I'$ to show that $\frac{r'}{r}=\frac{s}{s-a}$ where $r$ and $r'$ are the radii of the incircle and excircle, respectively. Then use $\triangle IDB\sim\triangle BD'I' $ to show that $\frac{r}{s-c}=\frac{s-b}{r'}$ and finally combine the 2 relations. Note that $BD=s-b$ which is similar to what you proved in (1).

Answer 2

b)

Clearly $BD' = BE' = z'$ and $CE' = CF' = y'$. Then, because $AF'= AD'$ we have $$x+z+y' =x+y+z'\implies z-z' = y-y'$$

But $$y+z = y'+z'$$

So adding these two you get $z=z'$ and $y=y'$ so $$AD' = x+y+z' = AB+BE'$$ and

$$x+y+z' = x+y+z = s$$

Answer 3

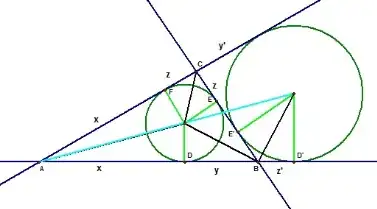
The incircle divides $BC$ in the ratio between the cotangents of half the triangle's interior angles at $B$ and $C$, while the excircle opposite $A$ divides $BC$ in the ratio of the cotangents of half the exterior angles there. But interior and exterior angles are supplementary, so their half-angles are complementary, and the cotangents of a half-interior and half-exterior angle must be reciprocals of each other. This is why the incircle and excircle divide $BC$ in the reverse ratio of each other.

To unpack that: the points of contact with the incircle (at $E$) and the excircle (at $E'$) divide the line $BC$ in the reverse ratio to each other; that is, $BE=CE'$, $CE'=BE$, so that the points $E$ and $E'$ are mirror images across the midpoint of $BC$. This gets you what you want since the circle theorem "tangents from a point are equal" tells you that $y'=CE'=BE=BD=y$ and $z'=BE'=CE=CF=z$.

We need two preliminary facts: the tan of a complementary angle is the reciprocal of the tan of that angle (so $\tan(90°-x)$, often written as the cotangent, $\cot(x)$, equals $1/\tan(x)$; replace $90°$ by $\pi/2$ if you know radian measure); and if two tangents to a circle of radius $R$ meet at an angle $\theta$ then the length of those tangents is $R \cot(\theta/2)$ (proof given below).

So for example $BE$ and $BD$ are tangents to the incircle (radius $r$) which meet at angle $\angle ABC$ so have length $y = r \cot (\angle ABC/2)$. Similarly $CE$ and $CF$ are tangents of length $z = r \cot(\angle BCA/2)$. Hence $E$ divides $BC$ in the ratio $$BE:EC = y:z = r \cot (\angle ABC/2): r \cot(\angle BCA/2)$$

We can cancel $r$ and use the trig identity $\cot(x)=1/\tan(x)$ to obtain

$$y:z = \frac{1}{\tan (\angle ABC/2)}: \frac{1}{\tan(\angle BCA/2)} = \tan(\angle BCA/2) : \tan (\angle ABC/2) $$

On the other hand, $BE'$ is a tangent to the excircle (radius $r'$) that meets another tangent of the same length $z'$ at the exterior angle at $B$, which is $180° - \angle ABC$. Therefore $$z' = r' \cot\left(\frac{180° - \angle ABC}{2}\right)=r' \cot(90° - \angle ABC/2) = r' \tan(\angle ABC/2)$$

where we used the complementary angle identity for $\cot$. Similarly $CE'$ has length $y'= r' \tan(\angle BCA/2)$, so by cancelling $r'$ we see $E'$ divides $BC$ in the ratio

$$BE':E'C = z':y' = \tan (\angle ABC/2) : \tan(\angle BCA/2)$$

Hence $E$ divides $BC$ in the reverse ratio to $E'$ and we must have $z=z'$ and $y=y'$.

---

Proof for length of two tangents meeting at angle $\theta$:

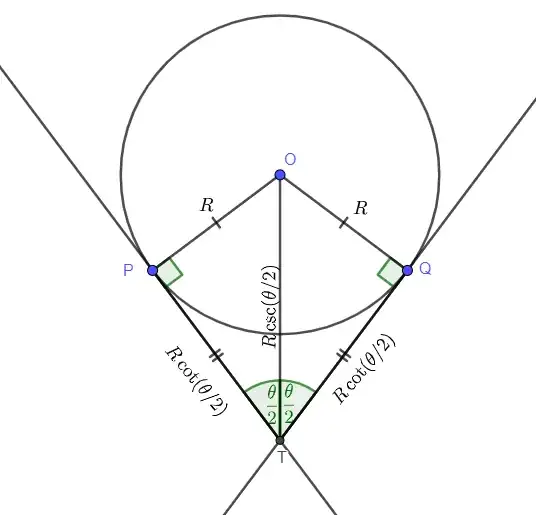
Let $P$ and $Q$ be points on a circle of centre $O$ and radius $R$, and tangents $PT$ and $QT$ meet at an angle $\angle PTQ = \theta$. Then triangles $\triangle OPT$ and $\triangle OQT$ are congruent by RHS since they have right-angles at $\angle OPT$ and $\angle OQT$ (radius is perpendicular to tangent), a common hypotenuse $OT$, and equal legs $OP=OQ=R$. Therefore angles $\angle OTP$ and $\angle OTQ$ must be equal, but they sum to $\theta$ so both must be $\theta/2$. Applying basic trigonometry to $\triangle OPT$ we have

$$\tan(\theta/2) = \frac{R}{PT} \implies PT = \frac{R}{\tan(\theta/2)} = R \cot(\theta/2)$$

and we can also find the length $OT$,

$$\sin(\theta/2) = \frac{R}{OT} \implies OT = \frac{R}{\sin(\theta/2)} = R \csc(\theta/2)$$

The above proof also establishes that the centre of the circle lies on the angle bisector, a fact we use a lot in incircle/excircle questions. See e.g. this geometric proof of $xyz = r^2(x+y+x)$, based on constructing a rectangle composed of right-angled triangles similar to those formed by the tangents to the incircle as in the construction above.