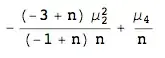Variance of sample variance?

Question

What is the variance of the sample variance? In other words I am looking for $\mathrm{Var}(S^2)$.

I have started by expanding out $\mathrm{Var}(S^2)$ into $E(S^4) - [E(S^2)]^2$

I know that $[E(S^2)]^2$ is $\sigma$ to the power of 4. And that is as far as I got.

Answer 1

Here's a general derivation that does not assume normality.

Let's rewrite the sample variance $S^2$ as an average over all pairs of indices: $$S^2={1\over{n\choose 2}}\sum_{\{i,j\}} {1\over2}(X_i-X_j)^2.$$ Since $\mathbb{E}[(X_i-X_j)^2/2]=\sigma^2$, we see that $S^2$ is an unbiased estimator for $\sigma^2$.

The variance of $S^2$ is the expected value of $$\left({1\over{n\choose 2}}\sum_{\{i,j\}} \left[{1\over2}(X_i-X_j)^2-\sigma^2\right]\right)^2.$$

When you expand the outer square, there are 3 types of cross product terms $$\left[{1\over2}(X_i-X_j)^2-\sigma^2\right] \left[{1\over2}(X_k-X_\ell)^2-\sigma^2\right]$$ depending on the size of the intersection $\{i,j\}\cap\{k,\ell\}$.

1. When this intersection is empty, the factors are independent and the expected cross product is zero.

2. There are $n(n-1)(n-2)$ terms where $|\{i,j\}\cap\{k,\ell\}|=1$ and each has an expected cross product of $(\mu_4-\sigma^4)/4$.

3. There are ${n\choose 2}$ terms where $|\{i,j\}\cap\{k,\ell\}|=2$ and each has an expected cross product of $(\mu_4+\sigma^4)/2$.

Putting it all together shows that $$\mbox{Var}(S^2)={\mu_4\over n}-{\sigma^4\,(n-3)\over n\,(n-1)}.$$ Here $\mu_4=\mathbb{E}[(X-\mu)^4]$ is the fourth central moment of $X$.

Answer 2

Maybe, this will help. Let's suppose the samples are taking from a normal distribution. Then using the fact that $\frac{(n-1)S^2}{\sigma^2}$ is a chi squared random variable with $(n-1)$ degrees of freedom, we get $$\begin{align*} \text{Var}~\frac{(n-1)S^2}{\sigma^2} & = \text{Var}~\chi^{2}_{n-1} \\ \frac{(n-1)^2}{\sigma^4}\text{Var}~S^2 & = 2(n-1) \\ \text{Var}~S^2 & = \frac{2(n-1)\sigma^4}{(n-1)^2}\\ & = \frac{2\sigma^4}{(n-1)}, \end{align*}$$

where we have used that fact that $\text{Var}~\chi^{2}_{n-1}=2(n-1)$.

Hope this helps.

Answer 3

There can be some confusion in defining the sample variance ... 1/n vs 1/(n-1). The OP here is, I take it, using the sample variance with 1/(n-1) ... namely the unbiased estimator of the population variance, otherwise known as the second h-statistic:

h2 = HStatistic[2][[2]] 

These sorts of problems can now be solved by computer. Here is the solution using the mathStatica add-on to Mathematica. In particular, we seek the Var[h2], where the variance is just the 2nd central moment, and express the answer in terms of central moments of the population:

CentralMomentToCentral[2, h2] 

We could just as easily find, say, the 4th central moment of the sample variance, as:

CentralMomentToCentral[4, h2]

Answer 4

This is quite a well-known result in statistics, and it can be found in a number of books and papers on sampling theory. You can find a range of useful moment results of this kind in O'Neill (2014) (this one is given in Result 3, p. 284). Consider a distribution with mean $\mu$, variance $\sigma^2$, skewness $\gamma$ and kurtosis $\kappa$ (where all these moments are finite).$^\dagger$ Taking $n$ IID draws from this distribution and taking the variance of the sample variance $S_n^2$ gives:

$$\boxed{\mathbb{V}(S_n^2) = \bigg( \kappa - \frac{n-3}{n-1} \bigg) \frac{\sigma^4}{n}}$$

In the special case where the underlying distribution is mesokurtic (e.g., for a normal distribution) we have $\kappa = 3$ and this expression then reduces to:

$$\mathbb{V}(S_n^2) = \frac{2n}{n-1} \cdot \frac{\sigma^4}{n} = \frac{2 \sigma^4}{n-1}.$$

You might also be interested to note that, in general, the sample variance and sample mean are correlated. Their covariance is $\mathbb{Cov}(\bar{X}_n, S_n^2) = \gamma \sigma^3/n$ and their corresponding correlation coefficient is:

$$\begin{align} \mathbb{Corr}(\bar{X}_n, S_n^2) &= \frac{\mathbb{Cov}(\bar{X}_n, S_n^2)}{\mathbb{S}(\bar{X}_n) \cdot \mathbb{S}(S_n^2)} \\[6pt] &= \frac{\gamma \sigma^3}{n} \Bigg/ \frac{\sigma}{\sqrt{n}} \cdot \sqrt{ \Big( \kappa - \frac{n-3}{n-1} \Big) \frac{\sigma^4}{n}} \\[6pt] &= \frac{\gamma \sigma^3}{n} \Bigg/ \frac{\sigma^3}{n} \cdot \sqrt{\kappa - \frac{n-3}{n-1}} \\[6pt] &= \frac{\gamma}{\sqrt{\kappa - (n-3)/(n-1)}}, \\[6pt] \end{align}$$

and as $n \rightarrow \infty$ you get:

$$\mathbb{Corr}(\bar{X}_n, S_n^2) \rightarrow \frac{\gamma}{\sqrt{\kappa - 1}},$$

which is the adjusted skewness of the underlying distribution. You can find further discussion of moments of the sample moments (including correlation between them) in O'Neill (2014).

---

$^\dagger$ Actually, you can just assume that the kurtosis is finite, and this implies that all the lower-order moments are also finite.

Answer 5

Showing the derivation of $E(\left[{1\over2}(X-Y)^2-\sigma^2\right]^2) = (\mu_4+\sigma^4)/2$ of user940:

LHS:

$E(\left[{1\over2}(X-Y)^2-\sigma^2\right]^2) = E(\frac{1}{4}(X-Y)^4 - (X-Y)^2 \sigma^2 + \sigma^4) = E(\frac{1}{4}(X-Y)^4) - 2\sigma^2\sigma^2 + \sigma^4 = E(\frac{1}{4}(X-Y)^4) - \sigma^4 = \frac{1}{4}E(X^4 -4X^3Y +6X^2Y^2 -4XY^3 + Y^4) -\sigma^4 = \frac{1}{4}(2E(X^4) -8E(X)E(X^3) +6 E(X^2)(X^2)) - \sigma^4 = \frac{1}{2}(E(X^4)-4E(X)E(X^3) +3 E(X^2)(X^2) - 2\sigma^4)$

I use the fact that $E((x-y)^2) = 2\sigma^2$ here.

RHS:

$\require{cancel} (\mu_4+\sigma^4)/2 = \frac{1}{2}(E((X-\mu)^4) + \sigma^4) = \frac{1}{2}(E((X-E(X))^4) + \sigma^4) = \frac{1}{2}(E(X^4 -4X^3E(X) + 6X^2E(X)^2 -4XE(X)^3 + E(X)^4) + \sigma^4) = \frac{1}{2}(E(X^4 -4X^3E(X) + 6X^2E(X^2) - 6X^2\sigma^2 -4XE(X)(E(X^2)-\sigma^2) + (E(X^2)-\sigma^2)^2) + \sigma^4) = \frac{1}{2}(E(X^4) -4E(X)^3E(X) + 6E(X)^2E(X^2) - 6E(X)^2\sigma^2 -4E(X)^2(E(X^2)-\sigma^2) + (E(X^2)-\sigma^2)^2 + \sigma^4) = \frac{1}{2}(E(X^4) -4E(X)^3E(X) + 6E(X)^2E(X^2) - \cancel{6E(X)^2\sigma^2} -4E(X^2)E(X^2) +\cancel{4E(X^2)\sigma^2 +4E(X^2)\sigma^2} - 4\sigma^4 + E(X^2)^2-\cancel{2E(X^2)\sigma^2} + \sigma^4 + \sigma^4) = \frac{1}{2}(E(X^4) -4E(X)^3E(X) + 3E(X)^2E(X^2) - 2\sigma^4)$

I use the fact that $E(x) = \mu$ and that $E(x)^2 = E(x^2) - \sigma^2$

Now LHS = RHS.

Answer 6

I know that this question is very old but wanted to contribute nonetheless as I found it very hard to find a proof online that was satisfying enough, yet easy enough to follow. Proofs by induction are not constructive and do not tell you where the expression comes from in the first place.

While user940's answer is helpful, some parts are not very obvious, especially the first line and the later lines involving counting.

I have come up with a solution that is easier to follow and intuit, and I hope it helps others.

Let $\mu := \mathop{\mathbb{E}}\left(X_{i}\right)$ denote the population mean and $\mu_{k} := \mathop{\mathbb{E}}\left[(X_{i} - \mu)^{k}\right]$ denote the $k$th centered population moment. Notice that with this notation, $\mu_{2}$ is the population variance (what you are used to notating with $\sigma^2$, so $\mu_{2}^{2}$ would be the square of this (or $\sigma^{4}$).

Then, if the kurtosis exists, $$\begin{align} \boxed{\mathop{\mathrm{Var}}\left(S^{2}\right) = \frac{1}{n}\left(\mu_{4} - \frac{n - 3}{n - 1}\mu_{2}^{2}\right).} \end{align}$$

Beginning from the definition of sample variance: $$ S^{2} := \frac{1}{n - 1} \sum_{i = 1}^{n} (X_{i} - \bar{X})^{2}, $$ let us derive the following useful lemma:

Lemma (reformulation of $S^{2}$ as the average distance between two datapoints). Let $\mathbf{X}$ be a sample of size $n$ and $S^{2}$ be the sample variance. Then $$ S^{2} \equiv \frac{1}{2n (n - 1)} \sum_{i=1}^{n}\sum_{j=1}^{n} (X_{i} - X_{j})^{2}. $$

Proof. Pick some $X_{j}$ and note that: $$\begin{align} S^{2} &\equiv \frac{1}{n- 1} \sum_{i=1}^{n}(X_{i} - X_{j} + X_{j} - \bar{X})^{2} \\ \implies (n - 1)S^{2} &= \sum_{i=1}^{n}(X_{i} - X_{j})^{2} + 2 \sum_{i=1}^{n} (X_{i} - X_{j})(X_{j} - \bar{X}) + \sum_{i=1}^{n}(X_{j} - \bar{X})^{2}. \end{align}$$ Now sum this over $j$: $$\begin{align} n(n - 1)S^{2} &= \sum_{j=1}^{n}\sum_{i=1}^{n}(X_{i} - X_{j})^{2} + 2 \sum_{j=1}^{n} \sum_{i=1}^{n} (X_{i} - X_{j})(X_{j} - \bar{X}) + \sum_{j=1}^{n} \sum_{i=1}^{n}(X_{j} - \bar{X})^{2}. \end{align}$$ The final term is simply $n(n - 1)S^{2}$ again, so we have: $$\begin{align} \sum_{i=1}^{n}\sum_{j=1}^{n}(X_{i} - X_{j})^{2} &= - 2 \sum_{i=1}^{n} \sum_{j=1}^{n} (X_{i} - X_{j})(X_{j} - \bar{X}) \\ &= 2 \sum_{i=1}^{n} \sum_{j=1}^{n} (X_{j} - \bar{X} + \bar{X} - X_{i})(X_{j} - \bar{X}) \\ &= 2 \sum_{i=1}^{n} \sum_{j=1}^{n} (X_{j} - \bar{X})^{2} + 2 \sum_{i=1}^{n} (\bar{X} - X_{i}) \underbrace{\sum_{j=1}^{n} (X_{j} - \bar{X})}_{0} \\ &= 2n(n - 1)S^{2}, \end{align}$$ giving the result.

Using this Lemma, we can now find the sample variance. Let's begin by using a small trick: Let $Z_{i} := X_{i} - \mu$. This means that $\mathop{\mathbb{E}}\left(Z_{i}^{k}\right) = \mu_{k}$ gives you the $k$th central moment. This makes the algebra much easier.

Proceed as so: $$\begin{align} S^{2} &\equiv \frac{1}{2n(n - 1)}\sum_{i=1}^{n}\sum_{j=1}^{n} \left( \overbrace{(X_{i} - \mu)}^{Z_{i}} - \overbrace{(X_{j} - \mu)}^{Z_{j}}\right)^{2} \\ \implies \mathop{\mathrm{Var}}\left(S^{2}\right) &\equiv \mathop{\mathrm{Var}}\left[\frac{1}{2n(n - 1)} \left(\sum_{i=1}^{n} \sum_{j=1}^{n} \left(Z_{i}^{2} + Z_{j}^{2} - 2 Z_{i} Z_{j}\right)\right) \right] \\ &= \mathop{\mathrm{Var}}\left[\frac{1}{2n(n - 1)} \left(2n \sum_{i=1}^{n} Z_{i}^{2} - 2 \sum_{i=1}^{n}\sum_{j=1}^{n}Z_{i}Z_{j}\right)\right] \\ &= \mathop{\mathrm{Var}}\left[\frac{1}{n(n - 1)}\left(n \sum_{i=1}^{n} Z_{i}^{2} - \sum_{i=1}^{n}\sum_{j=1}^{n}Z_{i}Z_{j}\right)\right] \\ &= \frac{1}{n^{2}(n - 1)^{2}} \Bigg[ n^{2} \mathop{\mathrm{Var}}\left(\sum_{i=1}^{n}Z_{i}^{2}\right) + \mathop{\mathrm{Var}}\left(\sum_{i=1}^{n}\sum_{j=1}^{n} Z_{i} Z_{j}\right)\\ &\phantom{=} - 2 n \mathop{\mathrm{Cov}}\left(\sum_{i=1}^{n}Z_{i}^{2}, \sum_{i=1}^{n}\sum_{j=1}^{n}Z_{i} Z_{j}\right)\Bigg]. \tag{\(\bigstar\)} \end{align}$$

Now we must calculate each of these variances and covariances. For the first one, $$\begin{align} \mathop{\mathrm{Var}}\left(\sum_{i=1}^{n}Z_{i}^{2}\right) &= n \mathop{\mathrm{Var}}\left(Z_{1}^{2}\right) \\ &= n\left(\mathop{\mathbb{E}}\left(Z_{1}^{4}\right) - \mathop{\mathbb{E}}\left(Z_{1}^{2}\right)^{2}\right) \\ &= n(\mu_{4} - \mu_{2}^{2}). \tag{\(\blacktriangle\)} \end{align}$$ (Note that $\mu_{2}^{2}$ is the variance squared.)

For the second variance, $$\begin{align} \mathop{\mathrm{Var}}\left(\sum_{i=1}^{n}\sum_{j=1}^{n}Z_{i} Z_{j}\right) &= \mathop{\mathbb{E}}\left(\left(\sum_{i=1}^{n}\sum_{j=1}^{n} Z_{i}Z_{j}\right)^{2}\right) - \mathop{\mathbb{E}}\left(\sum_{i=1}^{n}\sum_{j=1}^{n} Z_{i}Z_{j}\right)^{2}. \end{align}$$

To find the first expectation, we write: $$\begin{align} \mathop{\mathbb{E}}\left(\left(\sum_{i=1}^{n}\sum_{j=1}^{n} Z_{i}Z_{j}\right)^{2}\right) &= \sum_{i=1}^{n}\sum_{j=1}^{n}\sum_{k=1}^{n}\sum_{l=1}^{n} \mathop{\mathbb{E}}\left(Z_{i}Z_{j}Z_{k}Z_{l}\right). \end{align}$$

To compute this, we must consider all the possible ways that the indices $(i,j,k,l)$ could be different. If there is any index that is different from all the other indices, then the expectation is zero. Thus, the only way for $\mathop{\mathbb{E}}\left(Z_{i}Z_{j}Z_{k}Z_{l}\right)$ to be non-zero is if all indices are the same, or if there are two distinct pairs of equal indices (e.g. $i = j \neq k = l$).

In the first case, the expectation becomes $\mathop{\mathbb{E}}\left(Z_{i}^{4}\right) = \mu_{4}$, and there are $n$ ways that this happens.

In the second case, suppose $i = j$ and $k = l$ and $k > i$ (We take one to be strictly larger to avoid double counting in what follows). Then the expectation becomes $\mathop{\mathbb{E}}\left(Z_{i}^{2} Z_{k}^{2}\right) = \mathop{\mathbb{E}}\left(Z_{i}^{2}\right) \mathop{\mathbb{E}}\left(Z_{k}^{2}\right) = \mu_{2}^{2}$. The number of ways for $i = j > k = l$ is ${n \choose 2} = \frac{1}{2}n(n - 1)$. But there are other ways of choosing two pairs. In particular, there are ${4 \choose 2} = 6$ ways of choosing two pairs of indices from 4 indices, giving a total of $3n(n - 1)$ ways that the expectation equals $\mu_{2}^{2}$. Thus, $\mathop{\mathbb{E}}\left(\left(\sum_{i=1}^{n}\sum_{j=1}^{n} Z_{i}Z_{j}\right)^{2}\right) = n \mu_{4} + 3n(n - 1)\mu_{2}^{2}$.

Now we must calculate the expectation $\mathop{\mathbb{E}}\left(\sum_{i=1}^{n}\sum_{j=1}^{n}Z_{i}Z_{j}\right) = \sum_{i=1}^{n}\sum_{j=1}^{n}\mathop{\mathbb{E}}\left(Z_{i}Z_{j}\right)$. Since $Z_{i}$ and $Z_{j}$ are independent, $\mathop{\mathbb{E}}\left(Z_{i}Z_{j}\right) = 0$ whenever $i \neq j$. Thus, the expectation becomes $\mathop{\mathbb{E}}\left(\sum_{i=1}^{n}\sum_{j=1}^{n}Z_{i}Z_{j}\right) = \mathop{\mathbb{E}}\left(\sum_{i=1}^{n}Z_{i}^{2}\right) = n \mu_{2}$.

Subtracting $\mathop{\mathbb{E}}\left(\sum_{i=1}^{n}\sum_{j=1}^{n}Z_{i}Z_{j}\right)^{2} = n^{2}\mu_{2}^{2}$ from the previous expectation, we have: $$\begin{align} \mathop{\mathrm{Var}}\left(\sum_{i=1}^{n}\sum_{j=1}^{n}Z_{i}Z_{j}\right) &= n \mu_{4} + 2 n^{2} \mu_{2}^{2} - 3n \mu_{2}^{2}. \tag{\(\spadesuit\)} \end{align}$$

Finally, we calculate the covariance: $$\begin{align} \mathop{\mathrm{Cov}}\left(\sum_{i=1}^{n}Z_{i}^{2}, \sum_{i=1}^{n}\sum_{j=1}^{n}Z_{i}Z_{j}\right) &= \mathop{\mathbb{E}}\left(\sum_{i=1}^{n}\sum_{j=1}^{n}\sum_{k=1}^{n}Z_{i}^{2}Z_{j}Z_{k}\right) - \mathop{\mathbb{E}}\left(\sum_{i=1}^{n}Z_{i}^{2}\right)\mathop{\mathbb{E}}\left(\sum_{i=1}^{n}\sum_{j=1}^{n}Z_{i}Z_{j}\right). \end{align}$$

We have already found that the final two expectations are equal to $n \mu_{2}$, so the second term becomes $n^{2} \mu_{2}^{2}$.

For $\sum_{i=1}^{n}\sum_{j=1}^{n}\sum_{k=1}^{n} \mathop{\mathbb{E}}\left(Z_{i}^{2}Z_{j}Z_{k}\right)$, notice that the expectation is $0$ whenever $j \neq k$. When $i = j = k$, the expectation is $\mathop{\mathbb{E}}\left(Z_{1}^{4}\right) = \mu_{4}$ and there are $n$ ways of achieving this. When $i \neq j = k$, the expectation is $\mu_{2}^{2}$ and there are $n(n - 1)$ ways of achieving this (now the order of $i, j$ matters, so we do double count).

We therefore get: $$\begin{align} \mathop{\mathrm{Cov}}\left(\sum_{i=1}^{n}Z_{i}^{2}, \sum_{i=1}^{n}\sum_{j=1}^{n}Z_{i}Z_{j}\right) &= n(\mu_{4} - \mu_{2}^{2}). \tag{\(\clubsuit\)} \end{align}$$

Substituting $\clubsuit, \spadesuit, \blacktriangle$ the values we just found into $\bigstar$, we get $$\begin{align} \mathop{\mathrm{Var}}\left(S^{2}\right) &= \frac{1}{n^{2}(n - 1^{2})} \left[(n^{3} - 2n^{2} + n)\mu_{4} - (n^{3} - 4n^{2} + 3n) \mu_{2}^{2}\right] \\ &= \frac{1}{n^{2}(n - 1)^{2}} \left[n(n - 1)^{2} \mu_{4} - n(n - 1)(n - 3)\mu_{2}^{2}\right] \\ &= \frac{1}{n} \left(\mu_{4} - \frac{n - 3}{n - 1} \mu_{2}^{2}\right) \end{align}$$

Answer 7

I will use this as an example of this theorem(from Seber, G.A. and Lee, A.J. (2012))
Let $X_1, X_2, ... , X_n$ be independent rvs with means $(\theta_1, \theta_2, ... ,\theta_n)$,common $\mu_2,\mu_3,\mu_4$. If A is any n x n symmetric matrix and $a$ is a column vector of the diagonal elements of A, then
$$var[X'AX]=(\mu_4-3\mu^2_2)a'a+2\mu^2_2tr(A^2)+4\mu_2\theta'A^2\theta+4\mu_3\theta'Aa $$ denote $1_n$ as n-dim column vector that all elements are 1, notice that for sample variance $$S^2=\frac{1}{n-1}X'AX, where A=I_n-\frac{1}{n}1_n1_n' $$ and we have$A^2=A$, $a=(1-\frac{1}{n})1_n$
since $X_i$ in our case are iid, let's say their mean is $\mu$, then $\theta=\mu1_n$
so the third and fourth term is $0$,since $$ A^2\theta=A\theta=\mu(1_n-\frac{1}{n}1_n(1_n'1_n))=0\\ Aa=(1-\frac{1}{n})(1_n-\frac{1}{n}1_n(1_n'1_n))=0 $$ then$$ var[S^2]=\frac{1}{(n-1)^2}[(\mu_4-3\mu_2^2)(1-\frac{1}{n})^2n+2\mu_2^2(n-1)]=\frac{\mu_4}{n}-\frac{n-3}{n(n-1)}\mu_2^2 $$