Integral $\int_{-1}^1\frac1x\sqrt{\frac{1+x}{1-x}}\ln\left(\frac{2\,x^2+2\,x+1}{2\,x^2-2\,x+1}\right) \mathrm dx$

Question

I need help with this integral:

$$I=\int_{-1}^1\frac1x\sqrt{\frac{1+x}{1-x}}\ln\left(\frac{2\,x^2+2\,x+1}{2\,x^2-2\,x+1}\right)\ \mathrm dx.$$

The integrand graph looks like this:

$\hspace{1in}$

The approximate numeric value of the integral: $$I\approx8.372211626601275661625747121...$$

Neither Mathematica nor Maple could find a closed form for this integral, and lookups of the approximate numeric value in WolframAlpha and ISC+ did not return plausible closed form candidates either. But I still hope there might be a closed form for it.

I am also interested in cases when only numerator or only denominator is present under the logarithm.

Answer 1

I will transform the integral via a substitution, break it up into two pieces and recombine, perform an integration by parts, and perform another substitution to get an integral to which I know a closed form exists. From there, I use a method I know to attack the integral, but in an unusual way because of the 8th degree polynomial in the denominator of the integrand.

First sub $t=(1-x)/(1+x)$, $dt=-2/(1+x)^2 dx$ to get

$$2 \int_0^{\infty} dt \frac{t^{-1/2}}{1-t^2} \log{\left (\frac{5-2 t+t^2}{1-2 t +5 t^2} \right )} $$

Now use the symmetry from the map $t \mapsto 1/t$. Break the integral up into two as follows:

\begin{align} & 2 \int_0^{1} dt \frac{t^{-1/2}}{1-t^2} \log{\left (\frac{5-2 t+t^2}{1-2 t +5 t^2} \right )} + 2 \int_1^{\infty} dt \frac{t^{-1/2}}{1-t^2} \log{\left (\frac{5-2 t+t^2}{1-2 t +5 t^2} \right )} \\ &= 2 \int_0^{1} dt \frac{t^{-1/2}}{1-t^2} \log{\left (\frac{5-2 t+t^2}{1-2 t +5 t^2} \right )} + 2 \int_0^{1} dt \frac{t^{1/2}}{1-t^2} \log{\left (\frac{5-2 t+t^2}{1-2 t +5 t^2} \right )} \\ &= 2 \int_0^{1} dt \frac{t^{-1/2}}{1-t} \log{\left (\frac{5-2 t+t^2}{1-2 t +5 t^2} \right )} \end{align}

Sub $t=u^2$ to get

$$4 \int_0^{1} \frac{du}{1-u^2} \log{\left (\frac{5-2 u^2+u^4}{1-2 u^2 +5 u^4} \right )}$$

Integrate by parts:

$$\left [2 \log{\left (\frac{1+u}{1-u} \right )} \log{\left (\frac{5-2 u^2+u^4}{1-2 u^2 +5 u^4} \right )}\right ]_0^1 \\- 32 \int_0^1 du \frac{\left(u^5-6 u^3+u\right)}{\left(u^4-2 u^2+5\right) \left(5 u^4-2 u^2+1\right)} \log{\left (\frac{1+u}{1-u} \right )}$$

One last sub: $u=(v-1)/(v+1)$ $du=2/(v+1)^2 dv$, and finally get

$$8 \int_0^{\infty} dv \frac{(v^2-1)(v^4-6 v^2+1)}{v^8+4 v^6+70v^4+4 v^2+1} \log{v}$$

With this form, we may finally conclude that a closed form exists and apply the residue theorem to obtain it. To wit, consider the following contour integral:

$$\oint_C dz \frac{8 (z^2-1)(z^4-6 z^2+1)}{z^8+4 z^6+70z^4+4 z^2+1} \log^2{z}$$

where $C$ is a keyhole contour about the positive real axis. This contour integral is equal to (I omit the steps where I show the integral vanishes about the circular arcs)

$$-i 4 \pi \int_0^{\infty} dv \frac{8 (v^2-1)(v^4-6 v^2+1)}{v^8+4 v^6+70v^4+4 v^2+1} \log{v} + 4 \pi^2 \int_0^{\infty} dv \frac{8 (v^2-1)(v^4-6 v^2+1)}{v^8+4 v^6+70v^4+4 v^2+1}$$

It should be noted that the second integral vanishes; this may be easily seen by exploiting the symmetry about $v \mapsto 1/v$.

On the other hand, the contour integral is $i 2 \pi$ times the sum of the residues about the poles of the integrand. In general, this requires us to find the zeroes of the eight degree polynomial, which may not be possible analytically. Here, on the other hand, we have many symmetries to exploit, e.g., if $a$ is a root, then $1/a$ is a root, $-a$ is a root, and $\bar{a}$ is a root. For example, we may deduce that

$$z^8+4 z^6+70z^4+4 z^2+1 = (z^4+4 z^3+10 z^2+4 z+1) (z^4-4 z^3+10 z^2-4 z+1)$$

which exploits the $a \mapsto -a$ symmetry. Now write

$$z^4+4 z^3+10 z^2+4 z+1 = (z-a)(z-\bar{a})\left (z-\frac{1}{a}\right )\left (z-\frac{1}{\bar{a}}\right )$$

Write $a=r e^{i \theta}$ and get the following equations:

$$\left ( r+\frac{1}{r}\right ) \cos{\theta}=-2$$ $$\left (r^2+\frac{1}{r^2}\right) + 4 \cos^2{\theta}=10$$

From these equations, one may deduce that a solution is $r=\phi+\sqrt{\phi}$ and $\cos{\theta}=1/\phi$, where $\phi=(1+\sqrt{5})/2$ is the golden ratio. Thus the poles take the form

$$z_k = \pm \left (\phi\pm\sqrt{\phi}\right) e^{\pm i \arctan{\sqrt{\phi}}}$$

Now we have to find the residues of the integrand at these 8 poles. We can break this task up by computing:

$$\sum_{k=1}^8 \operatorname*{Res}_{z=z_k} \left [\frac{8 (z^2-1)(z^4-6 z^2+1) \log^2{z}}{z^8+4 z^6+70z^4+4 z^2+1}\right ]=\sum_{k=1}^8 \operatorname*{Res}_{z=z_k} \left [\frac{8 (z^2-1)(z^4-6 z^2+1)}{z^8+4 z^6+70z^4+4 z^2+1}\right ] \log^2{z_k}$$

Here things got very messy, but the result is rather unbelievably simple:

$$\operatorname*{Res}_{z=z_k} \left [\frac{8 (z^2-1)(z^4-6 z^2+1)}{z^8+4 z^6+70z^4+4 z^2+1}\right ] = \text{sgn}[\cos{(\arg{z_k})}]$$

EDIT

Actually, this is a very simple computation. Inspired by @sos440, one may express the rational function of $z$ in a very simple form:

$$\frac{8 (z^2-1)(z^4-6 z^2+1)}{z^8+4 z^6+70z^4+4 z^2+1} = -\left [\frac{p'(z)}{p(z)} + \frac{p'(-z)}{p(-z)} \right ]$$

where

$$p(z)=z^4+4 z^3+10 z^2+4 z+1$$

The residue of this function at the poles are then easily seen to be $\pm 1$ according to whether the pole is a zero of $p(z)$ or $p(-z)$.

END EDIT

That is, if the pole has a positive real part, the residue of the fraction is $+1$; if it has a negative real part, the residue is $-1$.

Now consider the log piece. Expanding the square, we get 3 terms:

$$\log^2{|z_k|} - (\arg{z_k})^2 + i 2 \log{|z_k|} \arg{z_k}$$

Summing over the residues, we find that because of the $\pm1$ contributions above, that the first and third terms sum to zero. This leaves the second term. For this, it is crucial that we get the arguments right, as $\arg{z_k} \in [0,2 \pi)$. Thus, we have

$$\begin{align}I= \int_0^{\infty} dv \frac{8 (v^2-1)(v^4-6 v^2+1)}{v^8+4 v^6+70v^4+4 v^2+1} \log{v} &= \frac12 \sum_{k=1}^8 \text{sgn}[\cos{(\arg{z_k})}] (\arg{z_k})^2 \\ &= \frac12 [2 (\arctan{\sqrt{\phi}})^2 + 2 (2 \pi - \arctan{\sqrt{\phi}})^2 \\ &- 2 (\pi - \arctan{\sqrt{\phi}})^2 - 2 (\pi + \arctan{\sqrt{\phi}})^2]\\ &= 2 \pi^2 -4 \pi \arctan{\sqrt{\phi}} \\ &= 4 \pi \, \text{arccot}{\sqrt{\phi}}\\\end{align}$$

Answer 2

$\large\hspace{3in}I=4\,\pi\operatorname{arccot}$$\sqrt\phi$

Answer 3

NEW ANSWER. I found yet another way of solving this problem. My new solution does not use contour integration, and is based on the following observation: for $|z| \leq 1$,

$$ - \int_{-1}^{1} \frac{1}{x} \sqrt{\frac{1+x}{1-x}} \log(1 - zx) \, dz= \pi \sin^{-1} z - \pi \log \left( \tfrac{1}{2}+\tfrac{1}{2}\sqrt{1-z^{2}} \right) . $$

As I want to keep both the old answer and the new answer, I posted my new solution to other page. You can check it here.

---

OLD ANSWER. Okay here is another solution. It is also related to my generalization.

We claim the following proposition:

Proposition. If $0 < r < 1$ and $r < s$, then $$ I(r, s) := \int_{-1}^{1} \frac{1}{x} \sqrt{\frac{1+x}{1-x}} \log \left( \frac{1 + 2rsx + (r^{2} + s^{2} - 1)x^{2}}{1 - 2rsx + (r^{2} + s^{2} - 1)x^{2}} \right) \, dx = 4\pi \arcsin r. \tag{1} $$

Assuming this proposition, all that we have to do is to solve the non-linear system of equations

$$ 2rs = 2 \quad \text{and} \quad r^{2} + s^{2} - 1 = 2. $$

The unique solution satisfying the condition of the proposition is $r = \phi - 1$ and $s = \phi$. So by $\text{(1)}$ we have

\begin{align*} \int_{-1}^{1} \frac{1}{x} \sqrt{\frac{1+x}{1-x}} \log \left( \frac{1 + 2x + 2x^{2}}{1 - 2x + 2x^{2}} \right) \, dx & = I(\phi-1, \phi) \\ &= 4\pi \arcsin (\phi - 1) = 4\pi \operatorname{arccot} \sqrt{\phi}. \end{align*}

Thus it remains to prove the proposition.

---

Proof of Proposition. We divide the proof into several steps.

Step 1. (Case reduction by analytic continuation) We first remark that given $r$ and $s$, we always have

$$ \min_{-1 \leq x \leq 1} \{ 1 \pm 2rsx + (r^{2} + s^{2} - 1)x^{2} \} > 0. \tag{2} $$

Indeed, it is not hard to check if we utilize the following equality

$$ 1 \pm 2rsx + (r^{2} + s^{2} - 1)x^{2} = (1 \pm rsx)^{2} - (1 - r^{2})(1 - s^{2}) x^{2}. $$

Then $\text{(2)}$ shows that the integrand of $I(r, s)$ remains holomoprhic under small perturbation of $s$ in $\Bbb{C}$. So it allows us to extend $s \mapsto I(r, s)$ as a holomorphic function on some open set containing the line segment $(r, \infty) \subset \Bbb{C}$. Then by the principle of analytic continuation, it is sufficient to prove that $\text{(1)}$ holds for $r < s < 1$.

Step 2. (Integral representation of $I$) Put $r = \sin \alpha$ and $s = \sin \beta$, where $ 0 < \alpha < \beta < \frac{\pi}{2}$. Then

\begin{align*} I(r, s) &= \int_{-1}^{1} \frac{1+x}{x\sqrt{1-x^{2}}} \log \left( \frac{1 + 2rsx + (r^{2} + s^{2} - 1)x^{2}}{1 - 2rsx + (r^{2} + s^{2} - 1)x^{2}} \right) \, dx \\ &= \int_{0}^{1} \frac{2}{x\sqrt{1-x^{2}}} \log \left( \frac{1 + 2rsx + (r^{2} + s^{2} - 1)x^{2}}{1 - 2rsx + (r^{2} + s^{2} - 1)x^{2}} \right) \, dx \qquad (\because \text{ parity}) \\ &= \int_{1}^{\infty} \frac{2}{\sqrt{x^{2}-1}} \log \left( \frac{x^{2} + 2rsx + (r^{2} + s^{2} - 1)}{x^{2} - 2rsx + (r^{2} + s^{2} - 1)} \right) \, dx \qquad (x \mapsto x^{-1}) \\ &= \int_{0}^{1} \frac{2}{t} \log \left( \frac{\left(t+t^{-1}\right)^{2} + 4rs\left(t+t^{-1}\right) + 4(r^{2} + s^{2} - 1)}{\left(t+t^{-1}\right)^{2} - 4rs\left(t+t^{-1}\right) + 4(r^{2} + s^{2} - 1)} \right) \, dt, \end{align*}

where in the last line we utilized the substitution $x = \frac{1}{2}(t + t^{-1})$. If we introduce the quartic polynomial \begin{align*} p(t) = t^{4} + 4rst^{3} + (4r^{2}+4s^{2}-2)t^{2} + 4rst + 1, \end{align*}

then by the property $p(1/t) = t^{-4}p(t)$, we can simplify

\begin{align*} I(r, s) &= 2 \int_{0}^{1} \frac{\log p(t) - \log p(-t)}{t} \, dt = \int_{0}^{\infty} \frac{\log p(t) - \log p(-t)}{t} \, dt \\ &= - \int_{0}^{\infty} \left( \frac{p'(t)}{p(t)} + \frac{p'(-t)}{p(-t)} \right) \log t \, dt = - \frac{1}{2} \Re \int_{-\infty}^{\infty} \left( \frac{p'(z)}{p(z)} + \frac{p'(-z)}{p(-z)} \right) \log z \, dz, \end{align*}

where we choose the branch cut of $\log$ in such a way that it avoids the upper-half plane

$$\Bbb{H} = \{ z \in \Bbb{C} : \Im z > 0 \}.$$

Step 3. (Residue calculation) Since

$$ f(z) := \left( \frac{p'(z)}{p(z)} + \frac{p'(-z)}{p(-z)} \right) \log z = O\left(\frac{\log z}{z^{2}} \right) \quad \text{as } z \to \infty, $$

by replacing the contour of integration by a semicircle of sufficiently large radius, it follows that

\begin{align*} I(r, s) = - \frac{1}{2} \Re \left\{ 2 \pi i \sum_{z_{0} \in \Bbb{H}} \operatorname{Res}_{z = z_{0}} f(z) \right\} = \pi \Im \sum_{z_{0} \in \Bbb{H}} \operatorname{Res}_{z = z_{0}} f(z). \end{align*}

(It turns out that $f(z)$ has only logarithmic singularity at the origin. So it does not account for the value of $I(r, s)$.) But by a simple calculation, together with the condition $ 0 < \alpha < \beta < \frac{\pi}{2}$, we easily notice that the zeros of $p(z)$ are exactly

$$ e^{\pm i(\alpha + \beta)} \quad \text{and} \quad -e^{\pm i(\alpha - \beta)}. $$

Now let $Z_{+}$ be the set of zeros of $p(z)$ in $\Bbb{H}$ and $Z_{-}$ be the set of zeros of $p(z)$ in $-\Bbb{H}$. Then

$$ Z_{+} = \{ e^{i(\beta+\alpha)}, -e^{-i(\beta - \alpha)} \} \quad \text{and} \quad Z_{-} = \{ e^{-i(\beta+\alpha)}, -e^{i(\beta- \alpha)} \}. $$

This in particular shows that

$$ \frac{p'(z)}{p(z)}\log z = \sum_{z_{0} \in Z_{+}} \frac{\log z}{z - z_{0}} + \text{holomorphic function on } \Bbb{H} $$

and

$$ \frac{p'(-z)}{p(-z)}\log z = -\sum_{z_{0} \in -Z_{-}} \frac{\log z}{z - z_{0}} + \text{holomorphic function on } \Bbb{H}. $$

So it follows that

\begin{align*} I(r, s) &= \pi \Im \left\{ \sum_{z_{0} \in Z_{+}} \log z_{0} - \sum_{z_{0} \in -Z_{-}} \log z_{0} \right\} \\ &= \pi \Im \left\{ \log e^{i(\beta+\alpha)} + \log e^{i(\pi-\beta+\alpha)} - \log e^{i(\pi-\beta-\alpha)} - \log e^{i(\beta-\alpha)} \right\} \\ &= \pi \Im \left\{ i(\beta+\alpha) + i(\pi-\beta+\alpha) - i(\pi-\beta-\alpha) - i(\beta-\alpha) \right\} \\ &= 4\pi \alpha = 4\pi \arcsin r. \end{align*}

This completes the proof.

Answer 4

Our aim is to give an elementary proof of Proposition formula (1) in the answer of @sos440. We first note that $$ \min_{-1\leq x\leq1}\{1\pm2rsx+(r^{2}+s^{2}-1)x^{2}\}>0. $$ Indeed, if $x=\pm1$ then $$ 1\pm2rsx+(r^{2}+s^{2}-1)x^{2}\geq(r-s)^{2}>0, $$ if $x=0$ then $$ 1\pm2rsx+(r^{2}+s^{2}-1)x^{2}=1>0, $$ if $-1<x<1$, $x\neq0$ then the equations \begin{eqnarray*} \frac{\partial}{\partial s}(1\pm2rsx+(r^{2}+s^{2}-1)x^{2}) & = & 0,\\ \frac{\partial}{\partial r}(1\pm2rsx+(r^{2}+s^{2}-1)x^{2}) & = & 0, \end{eqnarray*} give $\pm r=sx$, $\pm s=rx$, which is impossible.

In the second step we show that $I(r,s)$ is independent of $s$. $$ \frac{\partial}{\partial s}I(r,s)=\int_{-1}^{1}\sqrt{\frac{1+x}{1-x}}\cdot\frac{4r(1+(r^{2}-s^{2}-1)x^{2})}{(1-2rsx+(r^{2}+s^{2}-1)x^{2})(1+2rsx+(r^{2}+s^{2}-1)x^{2}}\, dx. $$ Substituting $x:=-x$ and adding them we obtain $$ 2\frac{\partial}{\partial s}I(r,s)=\int_{-1}^{1}\frac{2}{\sqrt{1-x^{2}}}\cdot\frac{4r(1+(r^{2}-s^{2}-1)x^{2})}{(1-2rsx+(r^{2}+s^{2}-1)x^{2})(1+2rsx+(r^{2}+s^{2}-1)x^{2}}\, dx, $$ that is, $$ \frac{\partial}{\partial s}I(r,s)=\int_{-1}^{1}\frac{1}{\sqrt{1-x^{2}}}\cdot\frac{4r(-s^{2}+r^{2}-1)x^{2}+4r}{1+(r^{2}+s^{2}-1)^{2}x^{4}+(2s^{2}-4r^{2}s^{2}+2r^{2}-2)x^{2}}\, dx. $$ Substituting $x:=\sin(t)$ we have $$ \frac{\partial}{\partial s}I(r,s) = \int_{-\pi/2}^{\pi/2}\frac{4r(-s^{2}+r^{2}-1)\sin(t)^{2}+4r}{1+(r^{2}+s^{2}-1)^{2}\sin(t)^{4}+(2s^{2}-4r^{2}s^{2}+2r^{2}-2)\sin(t)^{2}}\, dt $$ $$ =\int_{-\pi/2}^{\pi/2}-\frac{8r((-s^{2}+r^{2}-1)\cos(2t)+s^{2}-r^{2}-1)}{(r^{2}+s^{2}-1)^{2}\cos(2t)^{2}-2(r^{2}-s^{2}-1)(r^{2}+1-s^{2})\cos(2t)+r^{4}+(2-6s^{2})r^{2}+(s^{2}+1)^{2}}\, dt $$ $$ = \int_{-\pi}^{\pi}-\frac{4r((-s^{2}+r^{2}-1)\cos(y)+s^{2}-r^{2}-1)}{(r^{2}+s^{2}-1)^{2}\cos(y)^{2}-2(r^{2}-s^{2}-1)(r^{2}+1-s^{2})\cos(y)+r^{4}+(2-6s^{2})r^{2}+(s^{2}+1)^{2}}\, dy. $$ Introducing the new variable $T:=\tan\frac{y}{2}$ we obtain \begin{eqnarray*} \frac{\partial}{\partial s}I(r,s) & = & \int_{-\infty}^{\infty}-\frac{4r(s^{2}-r^{2})T^{2}-4r}{(r-s)^{2}(r+s)^{2}T^{4}+((2-4s^{2})r^{2}+2s^{2})T^{2}+1}\, dT\\ & = & -\frac{4r(s^{2}-r^{2})}{(r-s)^{2}(r+s)^{2}}\int_{-\infty}^{\infty}\frac{T^{2}+a}{T^{4}+bT^{2}+b^{2}/4+d}\, dT\\ & = & -\frac{4r(-s^{2}+r^{2})}{(r-s)^{2}(r+s)^{2}}\cdot\frac{(2a(b^{2}+4d)+(b^{2}+4d)^{3/2})\pi}{(b^{2}+4d)^{3/2}\sqrt{\sqrt{b^{2}+4d}+b}}, \end{eqnarray*} where $$ a=-\frac{1}{s^{2}-r^{2}}, $$ $$ b=\frac{(2-4s^{2})r^{2}+2s^{2}}{(r-s)^{2}(r+s)^{2}}, $$ $$ b^{2}+4d=\frac{4}{(r-s)^{2}(r+s)^{2}}. $$ It gives $2ab^{2}+8da+(b^{2}+4d)^{3/2}=0$.

Since $\frac{\partial}{\partial s}I(r,s)=0$ we have $$ I(r,s)=I(r,1)=\int_{-1}^{1}\frac{1}{x}\sqrt{\frac{1+x}{1-x}}\log\left(\frac{(1+rx)^{2}}{(1-rx)^{2}}\right)dx. $$ From this $$ \frac{\partial}{\partial r}I(r,1)=\int_{-1}^{1}\sqrt{\frac{1+x}{1-x}}\frac{4}{1-r^{2}x^{2}}\, dx. $$ Similarly as above we get $$ \frac{\partial}{\partial r}I(r,1)=\int_{-1}^{1}\frac{4}{\sqrt{1-x^{2}}(1-r^{2}x^{2})}\, dx=\frac{4\pi}{\sqrt{1-r^{2}}}=4\pi(\arcsin r)'. $$ It implies $$ I(r,1)=4\pi\arcsin r+C. $$ Taking the limit $\lim_{r\to0+}$ we obtain $C=0$, that is, $I(r,s)=4\pi\arcsin r$.

Answer 5

For the purposes of alternative methods, it may be of interest to note that the integrand

$$f(x)=\frac{1}{x}\sqrt{\frac{1+x}{1-x}}\log\left(\frac{2x^2+2x+1}{2x^2-2x+1}\right)$$ may be rewritten in terms of hyperbolic trigonometric functions. Using $$\tanh^{-1}(z) = \frac{1}{2}\log\left(\frac{1+z}{1-z}\right),$$ and we obtain

$$f(x)=\frac{1}{x}e^{\tanh^{-1}x}\log\left(\frac{1+\frac{2x}{1+2x^2}}{1-\frac{2x}{1+2x^2}}\right) = e^{\tanh^{-1} x}\left(\frac{2\tanh^{-1}\left(\frac{2x}{1+2x^2}\right)}{x}\right).$$

The rational function in the bracket, which we will denote $s(x)$, is symmetric about $x=0$.

The desired integral is

$$I=\int_{-1}^1 f(x)dx = \int_{-1}^1e^{\tanh^{-1}x}s(x)dx,$$

which, by adding the indicated useful definite integral to both side, gives

$$I + \int_{-1}^1 e^{-\tanh^{-1}x}s(x)dx = 2\int_{-1}^1 \frac{s(x)dx}{\sqrt{1-x^2}}.$$

Now using the change of variable $x=-y$ we have $$\int_{-1}^1 e^{-\tanh^{-1} x}s(x)dx = -\int_1^{-1} e^{\tanh y}s(-y)dy = \int_{-1}^1 e^{\tanh y}s(y)dy = I,$$ by the symmetry of $s(x)$. Hence, we finally obtain

$$I = \int_{-1}^1\frac{s(x)dx}{\sqrt{1-x^2}} = 2\int_{-1}^1\frac{1}{x\sqrt{1-x^2}}\tanh^{-1}\left(\frac{2x}{1+2x^2}\right)dx.$$

This integral is symmetric about $x=0$, so we have

$$I=4\int_0^1\frac{1}{x\sqrt{1-x^2}}\tanh^{-1}\left(\frac{2x}{1+2x^2}\right)dx,$$ which can be rewritten $$I=-4\int_0^1\left(\frac{d}{dx}\text{sech}^{-1}x\right)\tanh^{-1}\left(\frac{2x}{1+2x^2}\right)dx.$$

Using integration by parts this results in

$$I=8\int_0^1\frac{\text{sech}^{-1}(x)(1-2x^2)}{1+4x^4}dx.$$

---

We could also make the change of variable $y=\text{sech}^{-1}x$ to obtain

$$I=8\int_0^\infty\frac{y(\cosh^2(y)-2)\sinh y}{\cosh^4(y)+4}dy= 8\int_0^\infty\frac{y\sinh^3 y}{\cosh^4y+4}dy-8\int_0^\infty\frac{y\sinh y}{\cosh^4 y+4}dy.$$

Answer 6

This answer provides a way to find $I=\displaystyle\int_0^1\dfrac{\ln\left(x^4-2x^2+5\right)-\ln\left(5x^4-2x^2+1\right)}{1-x^2}\ dx$ (which @RonGordon obtained above) with differentiating under the integral sign. A $u$-substitution of $u=\dfrac{1+x^2}{1-x^2}$ yields this.

$$I=\dfrac{1}{2}\displaystyle\int_1^\infty\dfrac{\ln\left(\frac{u^2+2u+2}{u^2-2u+2}\right)}{\sqrt{u^2-1}}\ du.$$ Now integrate by parts with $a=\ln\left(\frac{u^2+2u+2}{u^2-2u+2}\right)$ and $db=\dfrac{du}{\sqrt{u^2-1}}.$ $$I=\left.\ln\left(\dfrac{u^2+2u+2}{u^2-2u+2}\right)\ln(u+\sqrt{u^2-1})\right]^\infty_1+2\displaystyle\int_1^\infty\dfrac{u^2-2}{u^4+4}\ln\left(u+\sqrt{u^2-1}\right)\ du$$ The first term is equal to $0$, so we are left with this. $$I=2\displaystyle\int_1^\infty\dfrac{u^2-2}{u^4+4}\ln\left(u+\sqrt{u^2-1}\right)\ du$$ We now begin the step of differentiating under the integral. Consider the following integral: $$f(a)=a\displaystyle\int_1^\infty\dfrac{x^2-a^2}{x^4+a^4}\ln\left(x+\sqrt{x^2-1}\right)\ dx$$ Note that trivially, $f(0)=0.$ A quick $u=\dfrac{x}{a}$ yields this. $$f(a)=\displaystyle\int_{\frac{1}{a}}^\infty\dfrac{u^2-1}{u^4+1}\ln\left(au+\sqrt{(au)^2-1}\right)\ du$$ Differentiating with respect to $a$ and using the Chain Rule, we get this. $$f'(a)=-1\times\dfrac{-1}{a^2}\times\dfrac{\left(\frac{1}{a}\right)^2-1}{\left(\frac{1}{a}\right)^4+1}\ln\left(a\left(\dfrac{1}{a}\right)+\sqrt{\left(a\left(\dfrac{1}{a}\right)\right)^2-1}\right)+\displaystyle\int_{\frac{1}{a}}^\infty\dfrac{x^2-1}{x^4+1}\times\dfrac{x}{\sqrt{(ax)^2-1}}\ dx$$ Luckily, the first term cancels, so we are left with this. $$f'(a)=\displaystyle\int_{\frac{1}{a}}^\infty\dfrac{x^2-1}{x^4+1}\times\dfrac{x}{\sqrt{(ax)^2-1}}\ dx$$ A $u$-substitution of $u=\sqrt{(ax)^2-1}$ yields this. $$f'(a)=\displaystyle\int_0^\infty\dfrac{u^2+1-a^2}{(u^2+1)^2+a^4}\ du$$ Consider the integral with $u\mapsto\dfrac{\sqrt{a^4+1}}{u}$ $$f'(a)=\dfrac{1}{\sqrt{a^4+1}}\displaystyle\int_0^\infty\dfrac{(1-a^2)u^2+(a^4+1)}{u^4+2u^2+(a^2+1)}\ du$$ If we add these two versions of the integral and divided the numerator and denominator of the integrand by $u^2$, we get the following. $$f'(a)=\dfrac{(1-a^2)+\sqrt{a^4+1}}{2\sqrt{a^4+1}}\times\displaystyle\int_0^\infty\dfrac{1+\frac{\sqrt{a^4+1}}{u^2}}{\left(u-\frac{\sqrt{a^4+1}}{u}\right)^2+2\left(1+\sqrt{a^4+1}\right)}\ du$$ We can finally perform a very nice substitution of $w=u-\dfrac{\sqrt{a^4+1}}{u}$ to solve this integral. $$f'(a)=\dfrac{(1-a^2)+\sqrt{a^4+1}}{2\sqrt{a^4+1}}\times\displaystyle\int_{-\infty}^\infty\dfrac{dw}{w^2+2\left(1+\sqrt{a^4+1}\right)}\ dw$$ Thus, we can finally say that $f'(a)=\dfrac{(1-a^2)+\sqrt{a^4+1}}{2\sqrt{a^4+1}}\times\dfrac{\pi}{\sqrt{2\left(1+\sqrt{a^4+1}\right)}}.$ After a bit of considerable algebra, we can simply that to obtain this. $$f'(a)=\dfrac{\pi}{2}\sqrt{\dfrac{\sqrt{a^4+1}-a^2}{a^4+1}}$$ Integrating, we can now say this about the value of $f(a).$ $$f(a)=\dfrac{\pi}{2}\displaystyle\int_0^a\sqrt{\dfrac{\sqrt{x^4+1}-x^2}{x^4+1}}\ dx$$ Only one $u$-substitution of $u=\sqrt{x^4+1}-x^2$ is required here to obtain this. $$f(a)=\dfrac{\pi}{2\sqrt{2}}\displaystyle\int_{\sqrt{a^4+1}-a^2}^1\dfrac{du}{\sqrt{1-u^2}}$$ This, of course, is equal to $\dfrac{\pi\arccos\left(\sqrt{a^4+1}-a^2\right)}{2\sqrt{2}}.$

We will now manipulate this result to a function with $\arctan$ in it.

$f(a)=\dfrac{\pi\arccos\left(\sqrt{a^4+1}-a^2\right)}{2\sqrt{2}}=\dfrac{\pi}{\sqrt{2}}\arctan\left(\sqrt{\dfrac{\sqrt{a^4+1}-1}{a^2}}\right)$

Our desired value for our original integral is $\sqrt{2}f\left(\sqrt{2}\right).$

$$\boxed{\displaystyle\int_0^1\dfrac{\ln\left(x^4-2x^2+5\right)-\ln\left(5x^4-2x^2+1\right)}{1-x^2}\ dx=\pi\arctan\left(\sqrt{\dfrac{\sqrt{5}-1}{2}}\right)=\pi\text{arccot}\sqrt{\phi}}$$

So the final answer to the original problem is $4\pi\text{arccot}\sqrt{\phi}.$

Answer 7

Noteworthy, RIES (http://mrob.com/pub/ries/index.html) finds closed form from numerical value in the form of an equation: $$ \cos{\left( \frac{x}{\pi} \right)}+1=\frac{2}{\phi^6}. $$

Simplifying above, we get another form of the result: $$ I = \pi \arccos{(17-8\sqrt{5})}. $$

Answer 8

Figured I would contribute and add a self-contained real analytic method:

I will use the following representations that are fairly straight-forward to prove: $$2\int_{0}^{\infty}\frac{\cos(x)-\cos(t \, x)}{x}\left(e^{-x\sqrt{-a-bi}}+e^{-x\sqrt{-a+bi}}\right) \, dx=\ln \left((t^2 -a)^2 + b^2\right)-\ln \left((1-a)^2+b^2\right)$$ $$\int_{0}^{\infty}\frac{\sin(x)}{x}\left(e^{-x\sqrt{-a-bi}}+e^{-x\sqrt{-a+bi}}\right) \, dx=\arctan\left(\frac{1}{\sqrt{-a-bi}}\right)+\arctan\left(\frac{1}{\sqrt{-a+bi}}\right)$$ $$\int_{0}^{\infty}\frac{\cos(t)-\cos(t \, x)}{x^2-1} \, dx=\frac{\pi}{2}\sin(t),\> \text{for} \, \> t\geq 0$$

Now we can begin evaluating $I$: $$I=\int_{-1}^{1}\frac{1}{x}\sqrt{\frac{1+x}{1-x}}\ln\left(\frac{2x^2+2x+1}{2x^2-2x+1}\right) \, dx$$

Enforce the substitution $\sqrt{\frac{1+x}{1-x}} = u$: $$\implies I = \int_{0}^{\infty}\frac{4u^2}{u^4-1}\ln\left(\frac{5u^4-2u^2+1}{u^4-2u^2+5}\right)\, du \stackrel{u \, \mapsto \frac{1}{u}}{=}\int_{0}^{\infty}\frac{4}{u^4-1}\ln\left(\frac{5u^4-2u^2+1}{u^4-2u^2+5}\right) \, du$$

From adding the two, we can deduce: $$I = \int_{0}^{\infty}\frac{2}{u^2-1}\ln\left(\frac{5u^4-2u^2+1}{u^4-2u^2+5}\right) \, du$$

Since $$\ln\left(5 u^4-2 u^2+1\right)-\ln(4)=\ln\left(\left(u^2-\frac{1}{5}\right)^2+\frac{4}{25}\right)-\ln\left(\frac{4}{5}\right)$$ $$\ln(u^4-2 u^2+5)-\ln(4)=\ln((u^2-1)^2+4)-\ln(4)$$

We can write $$A=\int_{0}^{\infty}\frac{2}{u^2-1}\left(\ln\left(\left(u^2-\frac{1}{5}\right)^2+\frac{4}{25}\right)-\ln\left(\frac{4}{5}\right)\right)\,du\\ B=\int_{0}^{\infty}\frac{2}{u^2-1}\left(\ln((u^2-1)^2+4)-\ln(4)\right)\, du$$ such that $I = A-B$

Now from the starting representations we deduce: $$\begin{align} \implies A &= \int_{0}^{\infty}\frac{4}{u^2-1}\int_{0}^{\infty}\frac{\cos(t)-\cos(u \, t)}{t}\left(e^{-t\sqrt{(-1-2i)/5}}+e^{-t\sqrt{(-1+2i)/5}}\right)\,dt\,du \\ &= 2\pi\int_{0}^{\infty}\frac{\sin(t)}{t}\left(e^{-t\sqrt{(-1-2i)/5}}+e^{-t\sqrt{(-1+2i)/5}}\right)\, dt \\ &= 2\pi\arctan\left(\frac{\sqrt{5}}{\sqrt{-1-2i}}\right)+2\pi\arctan\left(\frac{\sqrt{5}}{\sqrt{-1+2i}}\right) \\ &= \Re\left(4\pi \arctan\left(\frac{\sqrt{5}}{\sqrt{-1-2i}}\right)\right)\end{align}$$

Similarly, one finds $$B=\Re\left(4\pi\arctan\left(\frac{1}{\sqrt{-1-2i}}\right)\right)$$

By using the identity: $$\arctan (x)+\arctan (y)=\arctan \left(\frac{x+y}{1-x y}\right)$$

One deduces $$\boxed{I=4\pi \operatorname{arccot} \left(\sqrt{\phi}\right)}$$

Answer 9

This is not really an answer, but grossly too long for an comment. I didn't know how to simplify it beyond the final solution.

$$I=\int_{-1}^1 \frac{1}{x}\sqrt{\frac{1+x}{1-x}}\ln\left(\frac{2x^2+2x+1}{2x^2-2x+1}\right)\text{d}{x}$$

Begin with the substitution of $x=-\cos2a$ $$I=\int_{-1}^1 \frac{1}{-\cos2a}\sqrt{\frac{1-\cos2a}{1+\cos2a}}\ln\left(\frac{2\cos^2 2a-2\cos 2a+1}{2\cos^2 2a-2\cos2a+1}\right)\text{d}{x}$$

By the tangent and cos double angle properties

$$I=\int_{-1}^1 -\sec2a|\tan a|\ln\left(\frac{-2\cos^22a+\cos 4a+2}{2\cos2a+\cos4a+2}\right)\text{d}{a}$$

Were just getting started. Now replace $a=\frac{1}{2}\text{gd}(b)$ where $\text{gd}$ is the Gudermannian function.

$$I=\int_{-1}^1 -\sec(\text{gd}(b))|\tan(\text{gd}(\frac{b}{2}))|\ln\left(\frac{-2\cos^2(\text{gd}(b))+\cos (2\text{gd}(b))+2}{2\cos^2(\text{gd}(b))+\cos (2\text{gd}(b))+2}\right)\text{d}{a}$$

Hehe. Now we get to simplify a bit. This is under the definition of Gudermannian properties.

$$I=\int_{-1}^1 -\text{cosh}\space b|\sinh\frac{b}{2}|\ln\left(\frac{-2\text{sech}^2 b+(\text{sech}^2b+\tanh^2b)+2}{2\text{sech}^2 b+(\text{sech}^2b+\tanh^2b)+2}\right)$$

Now, use properties of $\tanh$ and $\text{sech} $ to simplify even further

$$I=\int_{-1}^1 -\text{cosh}\space b|\sinh\frac{b}{2}|\ln\left(\frac{(1-\text{sech}^2 b)+2}{(1+\text{sech}^2 b)+2}\right)$$

Our goal is to create an $\text{arctanh}$ function, but that will obviously take some serious effort. Factor out a $3$ to generate that $1$ needed even if it makes an ugly factoring.

$$I=\int_{-1}^1 -\text{cosh}\space b|\sinh\frac{b}{2}|\ln\left(\frac{3(1-\frac{\text{sech}^2 b}{3})}{3(1+\frac{\text{sech}^2 b}{3})}\right)$$

And now cut out all of the 3's. After this cut, use a property of $\ln$'s to reciprocate the argument of $\ln$. And multiply 2 and 1/2

$$I=\int_{-1}^1 2\text{cosh}\space b|\sinh\frac{b}{2}|\frac{1}{2}\ln\left(\frac{(1+\frac{\text{sech}^2 b}{3})}{(1-\frac{\text{sech}^2 b}{3})}\right)$$

And what do you know! You're there! Use a property of $\ln$ and $\text{arctanh}$ to generate a much CLEANER form (also by throwing the 2 in front).

$$I=2\int_{-1}^1 \text{cosh}\space b|\sinh\frac{b}{2}|\text{arctanh}(\frac{\text{sech}^2b}{3})$$

This function is even, and we can know that because all parts of what is above, $\cosh b,|\sinh b|, $ etc. all even. So we can do the following.

$$I=4\int_{0}^1 \text{cosh}\space b|\sinh\frac{b}{2}|\text{arctanh}(\frac{\text{sech}^2b}{3})$$

This is just an idea, and like I said not a real solution. I have no idea where to continue beyond this, but I thought it may help to come up with a new idea to solve.

Answer 10

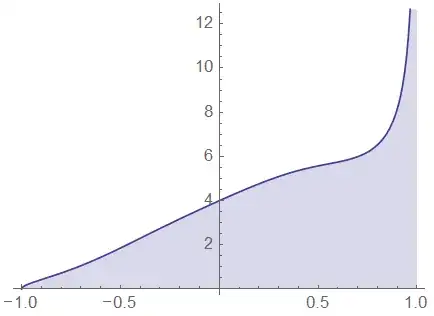
Well, 9 years later, this answer is going to be another approch via a contour integral. Denote $$I = \int_{-1}^{1} \frac{1}{x} \sqrt{\frac{1+x}{1-x}} \ln \left(\frac{2x^2+2x+1}{2x^2-2x+1}\right) \,\mathrm{d}x \in \mathbb{R}$$ our integral of interest.

Complex function

Let $$f(z) = \frac{1}{z} \sqrt{\frac{z+1}{z-1}}\left(\ln \left({\frac{2z+1+i}{2z-1+i}}\right) + \frac{\pi i}{2}\right),$$ where $\sqrt{w}$ and $\ln w$ are chosen such that they have a branch cut at the negative real axis (the so-called principal branches) in $w$-plane, that is $\arg w \in \left(-\pi,\pi\right]$. We denote $$h(z) = \frac{1}{z} \sqrt{\frac{z+1}{z-1}}, \qquad g(z) = \ln \left({\frac{2z+1+i}{2z-1+i}}\right) + \frac{\pi i}{2}$$ so $f(z) = h(z)g(z)$. To find the branch cuts of $f(z)$, we need to find which points on the $z$-plane are mapped onto the negative real axis in $w$. That is to solve

$$ \boxed{\sqrt{w}}_{B.C.}:\quad w=\frac{z+1}{z-1} = -t,\qquad t>0; \qquad\qquad \boxed{\ln w}_{B.C.}:\quad w=\frac{2z+1+i}{2z-1+i} = -t, \qquad t>0.$$ After simple manipulations, we arrive at $$ \boxed{h(z)}_{B.C.}:\quad z=\frac{t-1}{t+1} \in (-1,1); \qquad\qquad \boxed{g(z)}_{B.C.}:\quad z = \frac{t-1}{2(t+1)} - \frac{i}{2} \in \left(\frac{-1-i}{2},\frac{1-i}{2}\right).$$ where $(z_1,z_2)$ means here a line segment from $z_1$ to $z_2$ for any in general complex $z_1,z_2$.

Poles and residues

At $z\to \infty$, we have $f(z) = \frac{\pi i}{2z} + O(1/z^2)$, a simple pole. So $$\operatorname{Res}_\infty f(z) = - \lim_{z\to\infty} z f(z) = - \frac{\pi i}{2}.$$ Note that there is no pole at $z=0$ since $$\frac{2z+1+i}{2z-1+i} = -i-2iz+O(z^2),$$ so $$g(z) = -\frac{\pi i}{2}+2z + \frac{\pi i}{2} +O(z^2) = 2z +O(z^2),$$ which cancels the simple pole of $h(z)$ at $0 \pm 0i$.

Branch jumps

• $(-1,1):$ Let $t \in (-1,1)$. Since the complex square root function changes sign on the branch discontinuity, $h(t+i0) = -h(t-i0)$ and so $f(t+i0) = -f(t-i0)$.
• $\left(\frac{-1-i}{2},\frac{1-i}{2}\right):$ Let $t \in (-1/2,1/2)$. For $z = t - 1/2 i \pm i0,$ $$ \frac{2z+1+i}{2z-1+i} \bigg{|}_{t - i/2 \pm i0} = -r + \left(\frac{2z+1+i}{2z-1+i}\right)' \bigg{|}_{t - i/2} (\pm i0) = - r - \frac{4}{(1-2t)^2} (\pm i 0) = -r \mp i0.$$ where $-r$ is some negative number (branch cut mapped on negative numbers $-r$). Hence, $$g(t+i0) - g(t-i0) = \ln(-r-i0)-\ln(-r+i0) = -2\pi i.$$

Residue theorem

We integrate $f(z)$ along contour $C$ defined in Figure below. The contour is also split as $C = C_1 + \ldots + C_6$.

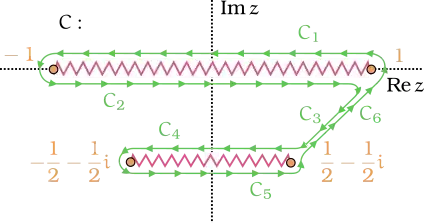
According to the Residue theorem, $$\oint_C f(z) \, \mathrm{d}x = - 2\pi i \operatorname{Res}_\infty f(z) = -\pi^2.$$

On the other hand, $$ \oint_C f(z) \, \mathrm{d}z = \sum_{k=1}^6 \int_{C_k} f(z) \, \mathrm{d}z. \tag{1}$$

Parametrisation

For $C_1, \ldots C_6$, we have the following parametrisation:

• $ \circleddash C_1: z = t + i0, t\in (-1,1), dz = dt$; Since $h(z)$ has a branch cut here, $f(t+i0) = h(t+i0)g(t)$. To obtain $h(t+i0)$, we first compute $$ \frac{z+1}{z-1}\bigg{|}_{t+i0} = \frac{z+1}{z-1}\bigg{|}_{t}+\left(\frac{z+1}{z-1}\right)'\bigg{|}_{t} i0 = -\frac{1+t}{1-t} - \frac{2}{(1-t)^2}i0 = -\frac{1+t}{1-t}-i0,$$ so $h(t+i0) = -\frac{i}{t} \sqrt{\frac{1+t}{1-t}}$. For $g(z)$, we can write $$ g(t) = \ln\left|\frac{2t+1+i}{2t-1+i}\right| + \arg\left(\frac{2t+1+i}{2t-1+i}\right) + \frac{\pi i}{2} = \frac12 \ln\left(\frac{2t^2+2t+1}{2t^2-2t+1}\right) + i \xi(t)$$ for some real function $\xi(t)$ which vanishes at $t=0$. Although we don't need this function, we express it anyway for completeness: Since $-\pi < \arg(2t+1+i)-\arg (2t-1+i) < \pi$, we have $\arg\left(\frac{2t+1+i}{2t-1+i}\right) = \arg(2t+1+i)-\arg (2t-1+i)$ and so $$ \xi(t) = \arctan\left(2t-1\right)-\arctan\left(2t+1\right) + \frac{\pi}{2}.$$ Overall, $$ f(t+i0) = - \frac{i}{t}\sqrt{\frac{1+t}{1-t}} \left( \frac12 \ln\left(\frac{2t^2+2t+1}{2t^2-2t+1}\right) + i \xi(t) \right) .$$ Hence $$ \int_{C_1} f(z) \, \mathrm{d}z = -\int_{\circleddash C_1} f(z) \, \mathrm{d}z = - \int_{-1}^{1} f(t+i0) \, \mathrm{d}t = \frac{i}{2}I - I_0,$$ where we denote $$I_0 = \int_{-1}^{1} \frac{\xi(t)}{t}\sqrt{\frac{1+t}{1-t}} \, \mathrm{d}t \in \mathbb{R}.$$
• $C_2$: Using knowledge of branchjumps, $$\int_{C_2} f(z) \, \mathrm{d}z = -\int_{\circleddash C_2} f(z) \, \mathrm{d}z = -\int_{C_1} (-f(z)) \, \mathrm{d}z = \frac{i}{2}I - I_0.$$
• $C_3 = \circleddash C_6$, so $$\int_{C_3} f(z) \, \mathrm{d}z + \int_{C_6} f(z) \, \mathrm{d}z = \int_{C_3} f(z) \, \mathrm{d}z - \int_{\circleddash C_6} f(z) \, \mathrm{d}z = 0$$
• $C_4$: Using knowledge of branchjumps, $$\int_{C_4} f(z) \, \mathrm{d}z = -\int_{\circleddash C_4} h(z)g(z) \, \mathrm{d}z = -\int_{C_5} h(z)(g(z)-2\pi i) \, \mathrm{d}z = -\int_{C_5} f(z) \, \mathrm{d}z + 2\pi i\int_{C_5} h(z) \, \mathrm{d}z.$$

Comparison & Antiderivative

Comparing the terms, that is by using $(1)$, we get $$-\pi^2 = iI - 2I_0 +2\pi i \int_{C_5} h(z) \, \mathrm{d}z.\tag{2}$$

We now solve the remaining integral $\int_{C_5} h(z) \, \mathrm{d}z$. For brevity, we denote $a = \frac{-1-i}{2}, b =\frac{1-i}{2}$, so $C_5 = (a,b)$. Notice $h(z)$ is now holomorphic in the vicinity of $C_5$. If we find its antiderivative $H(z)$ also holomorphic there, then

$$ \int_{C_5} h(z) \, \mathrm{d}z = H(b) - H(a).\tag{3}$$

This task is rather simple. First, we start by integrating $h(z)$ as if it was a real function. For $x>1$, we have by substitution $(x-1)/(x+1)=u^2$,

$$\int h(x) \, \mathrm{d}x = \int \frac{1}{x}\sqrt{\frac{x+1}{x-1}} \, \mathrm{d}x = \int \frac{4u^2}{u^4-1} \, \mathrm{d}u = 2\operatorname{argcoth}\left(\sqrt{\frac{x+1}{x-1}}\right) + 2\operatorname{arccot}\left(\sqrt{\frac{x+1}{x-1}}\right).$$

Hence, a suitable antiderivative in the complex plane is the following: $$H(z) = \ln \left(\frac{\sqrt{\frac{z+1}{z-1}}+1}{\sqrt{\frac{z+1}{z-1}}-1}\right) - i\ln \left(\frac{\sqrt{\frac{z+1}{z-1}}+i}{\sqrt{\frac{z+1}{z-1}}-i}\right).$$

We know the branch of $H(z)$ due to $\nu = \sqrt{\frac{z+1}{z-1}}$ is $z \in (-1,1)$. Assuming the principal branches, we now check where are the other possible branches of $H(z)$ due to $\ln$'s.

$$ \boxed{\ln{w}}_{B.C.}:\quad w=\frac{\nu+1}{\nu-1} = -t,\qquad t>0; \qquad\qquad \boxed{\ln w}_{B.C.}:\quad w=\frac{\nu+i}{\nu-i} = -t, \qquad t>0.$$ $$ \boxed{w(\nu)}_{B.C.}:\quad \nu = \frac{t-1}{t+1} = \in (-1,1) ; \qquad\qquad \boxed{w(\nu)}_{B.C.}:\quad \nu=i\frac{t-1}{t+1} \in (-i,i).$$ $$ \boxed{H(z)}_{B.C.}:\quad z = \frac{\nu^2+1}{\nu^2-1} \in (-\infty,0).$$

Hence, the B.C. of $H(z)$ lies at $(-\infty,1)$, safely away from $C_5$. Substituting $(3)$ into $(2)$, we get the value of $I$. And as a bonus, also $I_0$. For $I$,

$$ I = 2\pi\operatorname{Re} (H(a) - H(b)).\tag{4}$$

Substituing $a$ and $b$ into $\frac{z+1}{z-1}$, we get

$$\frac{a+1}{a-1} = -\frac{1}{5} + \frac{2i}{5} = \frac{1}{q^2}e^{2\alpha i}, \qquad \frac{b+1}{b-1}=-1+2i = q^2 e^{2\alpha i}$$ with $q = 5^{1/4}>1$ and $\alpha = \frac{\pi}{2} - \frac{1}{2}\arctan 2$. Note that $\pi/4 < \alpha < \pi/2$, so

$$\sqrt{\frac{a+1}{a-1}} = \frac{1}{q} e^{\alpha i}, \qquad \sqrt{\frac{b+1}{b-1}} = q e^{\alpha i}.$$

In the case of $b$, substituing into $\nu = \sqrt{\frac{z+1}{z-1}}$ and after simple manipulations, $$\frac{\nu + 1}{\nu - 1} \bigg{|}_{\nu = q e^{\alpha i}} = \frac{q^2-2 i q \sin\alpha-1}{q^2-2 q \cos\alpha+1}, \qquad \frac{\nu + i}{\nu - i} \bigg{|}_{\nu = q e^{\alpha i}} \frac{q^2+2 i q \cos\alpha-1}{q^2-2 q \sin\alpha+1}.$$

Hence, since the denominators are real, $$H(b) = \ln\left(q^2-2iq\sin\alpha-1\right)-\ln\left(q^2-2q\cos\alpha+1\right)-i\ln\left(q^2+2iq\cos\alpha-1\right)+i \ln\left(q^2-2q\sin\alpha+1\right),$$

expanding the logarithms into real and imaginary part, $$H(b) = \frac{1}{2} \ln\left(q^4-2 q^2 \cos (2 \alpha )+1\right)+i \arg \left(q^2-2 i q\sin\alpha-1\right)-\ln\left(q^2-2q\cos\alpha+1\right)-\frac{1}{2} i \ln\left(1+2q^2\cos (2 \alpha )+q^4\right)+\arg \left(q^2+2iq\cos\alpha-1\right)+i\ln\left(q^2-2q \sin\alpha+1\right)$$

Since we are interested only in real part (just $I$), $$\operatorname{Re} H(b) = \frac{1}{2} \ln\left(q^4-2 q^2 \cos (2 \alpha )+1\right)-\ln\left(q^2-2q\cos\alpha+1\right)+\arg \left(q^2+2iq\cos\alpha-1\right)$$

Similarly for $a$ (change $q$ to $1/q$). \begin{align*} \operatorname{Re} H(a) & = \frac{1}{2} \ln\left(\frac{1}{q^4}\!-\!\frac{2}{q^2} \cos (2 \alpha)\!+\!1\right)-\ln\left(\frac{1}{q^2}\!-\!\frac{2}{q}\cos\alpha\!+\!1\right)+\arg \left(\frac{1}{q^2}\!+\!\frac{2i}{q}\cos\alpha\!-\!1\right)\\ &= \frac{1}{2} \ln\left(q^4\!-\!2 q^2 \cos (2 \alpha )\!+\!1\right)-\ln\left(q^2\!-\!2q\cos\alpha\!+\!1\right)+\pi - \arg \left(q^2\!+\!2iq\cos\alpha\!-\!1\right). \end{align*}

Therefore, the grand finale, $$I = 4\pi \left(\frac{\pi}{2} - \arg \left(q^2\!+\!2iq\cos\alpha\!-\!1\right)\right) = 4\pi \operatorname{arccot} \frac{2q\cos\alpha}{q^2-1}.$$

To show this result is the same as the one found already, note that $$\left(\frac{2q\cos\alpha}{q^2-1}\right)^2 = \frac{4q^2\sin^2 \left(\frac{\pi}{2} -\alpha\right)}{(q^2-1)^2} = \frac{4\sqrt5\sin^2 \left(\frac12 \arctan 2\right)}{(\sqrt5-1)^2} = 2\sqrt5\,\frac{1-\frac{1}{\sqrt5}}{(\sqrt5-1)^2} = \frac{1+\sqrt5}{2}.$$

Answer 11

$\color{green}{\textbf{Version of 17.09.23.}}$

Let $\;y=\sqrt{\dfrac{1+x}{1-x}},\;$ then $\;x=\dfrac{1-y^2}{1+y^2},\;$ $$I=\int\limits_{-1}^1\dfrac1x\,\sqrt{\dfrac{1+x}{1-x}}\,\ln\,\dfrac{2x^2+2x+1}{2x^2-2x+1}\,\text dx = 4\int\limits_0^\infty \ln\,\dfrac{y^4-2y^2+5}{5y^4-2y^2+1}\,\dfrac{\text dy}{1-y^4}=I_0-I_1,$$ where $$I_0=2\int\limits_0^\infty \ln\,\dfrac{y^4-2y^2+5}{5y^4-2y^2+1}\,\dfrac{\text dy}{1-y^2},\quad I_1=2\int\limits_0^\infty \ln\,\dfrac{y^4-2y^2+5}{5y^4-2y^2+1}\,\dfrac{\text dy}{1+y^2}.\tag1$$ By the substitution $\;y=\dfrac1z\;$ easily to get $$\int\limits_1^\infty \ln\,\dfrac{y^4-2y^2+5}{5y^4-2y^2+1}\,\dfrac{\text dy}{1+y^2}=-\int\limits_0^1 \ln\,\dfrac{z^4-2z^2+5}{5z^4-2z^2+1}\,\dfrac{\text dz}{1+z^2}.$$ I.e. $$I_1=0.\tag2$$

On the other hand, $$I_{0}=I_{00}-I_{01},$$ where $$I_{00}=2\int\limits_0^\infty \ln\,\dfrac{y^4-2y^2+5}{(y^2+1)^2}\,\dfrac{\text dy}{1-y^2},\quad I_{01}=2\int\limits_0^\infty \ln\,\dfrac{5y^4-2y^2+1}{(y^2+1)^2}\,\dfrac{\text dy}{1-y^2},\tag3$$ By the substitution $\,y=\dfrac1z\,$ easily to get $$\int\limits_0^\infty \ln\,\dfrac{5y^4-2y^2+1}{(y^2+1)^2}\,\dfrac{\text dy}{1-y^2}=-\int\limits_0^\infty \ln\,\dfrac{z^4-2z^2+5} {(z^2+1)^2}\,\dfrac{\text dz}{1-z^2},$$ $$I_{01}=-I_{00},\quad I=2I_{00},\tag4$$

$$I=2I_{00}=4\int\limits_0^\infty \ln\,\dfrac{y^4-2y^2+5}{(y^2+1)^2}\,\dfrac{\text dy}{1-y^2}$$ $$=4\int\limits_0^\infty \dfrac{\ln(y^2-1-2i)+\ln(y^2-1+2i)-2\ln(y^2+1)}{1-y^2}\,\text dy$$ $$I=4(J(-1-2i)+J(-1+2i)-2J(1)),\tag5$$ where $$J(p)=\int\limits_0^\infty \dfrac{\ln(y^2+p)}{1-y^2}\,\text dy\tag6,$$ $$\dfrac{\,\text dJ(p)}{\,\text dp} =\int\limits_0^\infty \dfrac{\,\text dy}{(y^2+p)(1-y^2)} =\dfrac{F_1+F_2(p)}{1+p},$$ $$F_1=\int\limits_0^\infty \dfrac1{1-y^2}\,\text dy,\quad F_2(p)=\int\limits_0^\infty \dfrac1{y^2+p}\,\text dy.$$ By the substitution $\,y=\dfrac1t\,$ easily to get $$\int\limits_0^1 \dfrac1{1-y^2}\,\text dy =-\int\limits_1^\infty \dfrac1{1-t^2}\,\text dt,\quad F_1=0.$$ At the same time, $$F_2(p)=\dfrac1{\sqrt p}\,\arctan\dfrac{y}{\sqrt p}\bigg|_0^\infty =\dfrac \pi{2\sqrt p}.$$ Therefore, $$\dfrac{\,\text dJ(p)}{\,\text dp}=\dfrac\pi{2(1+p)\sqrt p},$$ $$J(p)=\int\dfrac\pi{1+p}\,\dfrac{\,\text dp}{2\sqrt p}=\pi \arctan \sqrt p + \text C.$$ From $(5)$ should $$\begin{align} &I=4\pi\left(\arctan\sqrt{-1-2i}+\arctan\sqrt{-1+2i} -2\arctan1\right)\\[4pt] &=4\pi\left(\arctan\dfrac{\sqrt{-1-2i}+\sqrt{-1+2i}}{1-\sqrt5} -\dfrac\pi2\right) =4\pi\left(\arctan\dfrac{\sqrt{2(\sqrt5-1)}}{1-\sqrt5} -\dfrac\pi2\right)\\[4pt] &=4\pi\left(\arctan\left(-\sqrt{\dfrac{\sqrt5+1}2}\right) -\dfrac\pi2\right) =4\pi\left(\pi-\arctan\sqrt{\dfrac{\sqrt5+1}2}-\dfrac\pi2\right),\\[4pt] &\color{green}{\mathbf{I=4\pi\operatorname{arccot}\sqrt{\varphi}\approx 8.37221162660127566162574712109841263808172805388220741371709,}} \end{align}$$ where $\;\varphi=\dfrac{\sqrt5+1}2\;$ is the golden ratio.

Answer 12

Eight years later.

Starting from @Ron Gordon's substitution $$8 \int_0^{\infty} \frac{(u^2-1)(u^4-6 u^2+1)}{u^8+4 u^6+70 u^4+4 u^2+1} \log(u)\,du$$ since the roots of the polynomials in $\color{red}{ u^2}$ are simple, we can use partial fraction decomposition (I shall not type the formulae) and we face four integrals $$I=\int \frac \alpha {\beta x^2+\gamma}\log(x)\,dx$$ where all coefficients are complex numbers. Then $$I=\frac{i \alpha \left(\text{Li}_2\left(\frac{i x \sqrt{\beta }}{\sqrt{\gamma }}\right)-\text{Li}_2\left(-\frac{i x \sqrt{\beta }}{\sqrt{\gamma }}\right)+\log (x) \left(\log \left(1-\frac{i \sqrt{\beta } x}{\sqrt{\gamma }}\right)-\log \left(1+\frac{i \sqrt{\beta } x}{\sqrt{\gamma }}\right)\right)\right)}{2 \sqrt{\beta\gamma }}$$ which make $$J=\int_0^\infty \frac \alpha {\beta x^2+\gamma}\log(x)\,dx=\frac{i \alpha \left(\log ^2\left(\frac{i \sqrt{\beta }}{\sqrt{\gamma }}\right)-\log ^2\left(-\frac{i \sqrt{\beta }}{\sqrt{\gamma }}\right)\right)}{4 \sqrt{\beta\gamma }}=-\frac{\pi \alpha \log \left(\frac{\beta }{\gamma }\right)}{4 \sqrt{\beta\gamma }}$$ This gives as a result $$8 \int_0^{\infty} \frac{(u^2-1)(u^4-6 u^2+1)}{u^8+4 u^6+70 u^4+4 u^2+1} \log(u)\,du=\pi \left(\pi -\cot ^{-1}\left(\frac{1}{4} \sqrt{22+17 \sqrt{5}}\right)\right)$$ I have not been able to simplify further.

Edit

If you look at this question of mine, @Jyrki Lahtonen made the simplification I was not able to do.

Answer 13

I have a relatively straightforward elementary approach.

First you use the substitution $x \rightarrow -x$ and add the integrals to obtain $$I=\int_{-1}^1\frac1x\frac{1}{\sqrt{1-x^2}}\ln\left(\frac{2\,x^2+2\,x+1}{2\,x^2-2\,x+1}\right)\ \mathrm dx.$$

A further substitution, $x\rightarrow\frac{2x}{1+x^2}$ yields

$$I=\int_{-1}^1\frac1x\ln\left(\frac{4 x^2+(x+1)^4}{4 x^2+(x-1)^4}\right)\ \mathrm dx=2\int_{-1}^1\frac1x\ln\left(4 x^2+(x+1)^4\right)\ \mathrm dx.$$

Define the function J by $$J(\lambda)=\int_{-1}^{1}\frac{\ln\left((x+1)^2+2\, i \,\lambda\, x\right)}{x} dx.$$ Then $$I=2(J(1)+J(-1)).$$

Differentiating under the integral sign gives $$J^{'}(\lambda)=2i\int_{-1}^{1}\frac{1}{\left((x+1)^2+2\, i \,\lambda\, x\right)} dx=\frac{i \pi}{\sqrt{\lambda^2-2i\lambda}}=\frac{i \pi}{\sqrt{1-(1+i\lambda)^2}}.$$

Hence $$J(\lambda)=\pi\arcsin(1+i\lambda)+C.$$ But $$J(0)=2\int_{-1}^{1}\frac{\ln\left(x+1\right)}{x} dx=\pi^2/2$$ which implies $C=0$, hence $$I=2\pi(\arcsin(1+I)+\arcsin(1-I))=4\pi\arcsin(\frac{1}{\phi})=4\,\pi\operatorname{arccot}\sqrt\phi$$ using standard identities.

Answer 14

Since this question receives a lot of answer recently, I thought I might partake as well. My solution to this historial question (on this site, at least) requires a lemma, namely: $$ \int_0^{\infty}{\frac{dx^2+e}{ax^4+bx^2+c}}\mathrm{d}x=\frac{ \pi}{2\sqrt{2\sqrt{ac}+b}}\left[ \frac{d}{\sqrt{a}}+\frac{e}{\sqrt{c}} \right] $$ This works for $a,b,c>0, d,e\in \mathbb{R}$. (the variable range can be larger, but this is enough for this question.) I shall provide a proof, too. The first time I derive this is though complex analysis, but here I will do it more elementarily.
To start with, assume $f$ is a even real function, then, \begin{align*} \int_{-\infty}^{\infty}{f\left( \frac{x}{p^2}-\frac{q^2}{x} \right) \mathrm{d}x}=&\underset{x=pqe^t}{\underbrace{\int_0^{\infty}{f\left( \frac{x}{p^2}-\frac{q^2}{x} \right) \mathrm{d}x}}}+\underset{x=pqe^{-t}}{\underbrace{\int_{-\infty}^0{f\left( \frac{x}{p^2}-\frac{q^2}{x} \right) \mathrm{d}x}}} \\ =&\int_{-\infty}^{\infty}{f\left( \frac{q}{p}\left( e^t-e^{-t} \right) \right) pqe^t\mathrm{d}t}+\int_{-\infty}^{\infty}{f\left( \frac{q}{p}\left( e^{-t}-e^t \right) \right) pqe^{-t}\mathrm{d}t} \\ =&\int_{-\infty}^{\infty}{f\left( 2\frac{q}{p}\sinh \left( t \right) \right) 2pq\cosh \left( t \right) \mathrm{d}t} \stackrel{2\frac{q}{p}\sinh \left( t \right) =x}{=}p^2\int_{-\infty}^{\infty}{f\left( x \right) \mathrm{d}x} \end{align*} So we have \begin{align*} &\int_0^{\infty}{\frac{dx^2+e}{ax^4+bx^2+c}}\mathrm{d}x=\frac{1}{2}\int_{-\infty}^{\infty}{\frac{dx^2+e}{ax^4+bx^2+c}}\mathrm{d}x \\ =&\frac{d}{2}\int_{-\infty}^{\infty}{\frac{x^2}{ax^4+bx^2+c}}\mathrm{d}x+\frac{e}{2}\int_{-\infty}^{\infty}{\frac{1}{ax^4+bx^2+c}}\mathrm{d}x \\ =&\frac{d}{2}\int_{-\infty}^{\infty}{\frac{x^2}{cx^4+bx^2+a}}\mathrm{d}x+\frac{e}{2}\int_{-\infty}^{\infty}{\frac{x^2}{ax^4+bx^2+c}}\mathrm{d}x \\ =&\frac{d}{2}\int_{-\infty}^{\infty}{\frac{1}{cx^2+b+\frac{a}{x^2}}}\mathrm{d}x+\frac{e}{2}\int_{-\infty}^{\infty}{\frac{1}{ax^2+b+\frac{c}{x^2}}}\mathrm{d}x \\ =&\frac{d}{2}\int_{-\infty}^{\infty}{\frac{1}{\left( \sqrt{c}x-\frac{\sqrt{a}}{x} \right) ^2+2\sqrt{ac}+b}}\mathrm{d}x+\frac{e}{2}\int_{-\infty}^{\infty}{\frac{1}{\left( \sqrt{a}x-\frac{\sqrt{c}}{x} \right) ^2+2\sqrt{ac}+b}}\mathrm{d}x \\ =&\frac{d}{2\sqrt{c}}\int_{-\infty}^{\infty}{\frac{1}{x^2+2\sqrt{ac}+b}}\mathrm{d}x+\frac{e}{2\sqrt{a}}\int_{-\infty}^{\infty}{\frac{1}{x^2+2\sqrt{ac}+b}}\mathrm{d}x \\ =&\frac{\pi}{2\sqrt{2\sqrt{ac}+b}}\left[ \frac{d}{\sqrt{a}}+\frac{e}{\sqrt{c}} \right] \end{align*}

---

Now, let's prove the integral at hand! Actually, let's prove a broader case. Given $r>\left| s \right|$, $$ \int_{-1}^1{\frac{1}{x}\sqrt{\frac{1+x}{1-x}}\ln \left( \frac{\left( 2r-1 \right) x^2+2sx+1}{\left( 2r-1 \right) x^2-2sx+1} \right)}\mathrm{d}x=4\pi \mathrm{sgn} \left( s \right) \mathrm{arcsin} \left( \sqrt{r-\sqrt{r^2-s^2}} \right) $$ notice that $I\left( r,0 \right) =0$ and $I\left( r,-s \right) =-I\left( r,s \right) $, therefore we can only consider the case where $s>0$ \begin{align*} I\left( r,s \right) =&\int_{-1}^1{\frac{1}{x}\sqrt{\frac{1+x}{1-x}}\ln \left[ \frac{\left( 2r-1 \right) x^2+2sx+1}{\left( 2r-1 \right) x^2-2sx+1} \right]}\mathrm{d}x \\ =&2\int_0^1{\frac{1}{x\sqrt{1-x^2}}\ln \left[ \frac{\left( 2r-1 \right) x^2+2sx+1}{\left( 2r-1 \right) x^2-2sx+1} \right]}\mathrm{d}x \\ \stackrel{(1)}{=}&2\int_0^{\frac{\pi}{2}}{\frac{1}{\cos \left( \theta \right)}\ln \left[ \frac{\left( 2r-1 \right) \cos ^2\left( \theta \right) +2s\cos \left( \theta \right) +1}{\left( 2r-1 \right) \cos ^2\left( \theta \right) -2s\cos \left( \theta \right) +1} \right]}\mathrm{d}\theta \\ \stackrel{(2)}{=}&4\int_0^1{\frac{1}{1-t^2}\ln \left[ \frac{\left( 2r-1 \right) \left( 1-t^2 \right) ^2+2s\left( 1-t^2 \right) \left( 1+t^2 \right) +\left( 1+t^2 \right) ^2}{\left( 2r-1 \right) \left( 1-t^2 \right) ^2-2s\left( 1-t^2 \right) \left( 1+t^2 \right) +\left( 1+t^2 \right) ^2} \right]}\mathrm{d}t \end{align*} Then differentiate \begin{align*} \partial_s I\left( r,s \right) =&4\int_0^1{\left[ \frac{1+t^2}{\left( r-s \right) t^4+\left( 2-2r \right) t^2+\left( r+s \right)}+\frac{1+t^2}{\left( r+s \right) t^4+\left( 2-2r \right) t^2+\left( r-s \right)} \right]}\mathrm{d}t \\ \stackrel{(3)}{=}&4\int_1^{\infty}{\left[ \frac{1+t^2}{\left( r+s \right) t^4+\left( 2-2r \right) t^2+\left( r-s \right)}+\frac{1+t^2}{\left( r-s \right) t^4+\left( 2-2r \right) t^2+\left( r+s \right)} \right]}\mathrm{d}t \\ =&2\int_0^{\infty}{\left[ \frac{1+t^2}{\left( r+s \right) t^4+\left( 2-2r \right) t^2+\left( r-s \right)}+\frac{1+t^2}{\left( r-s \right) t^4+\left( 2-2r \right) t^2+\left( r+s \right)} \right]}\mathrm{d}t \\ \stackrel{(4)}{=}&\frac{2\pi \left( \sqrt{r-s}+\sqrt{r+s} \right)}{\sqrt{r^2-s^2}\sqrt{2\sqrt{r^2-s^2}+2-2r}} \end{align*} Integrate again \begin{align*} I\left( r,\lambda \right) =\int_0^{\lambda}{\frac{\partial}{\partial s}I\left( r,s \right) \mathrm{d}s}=&\sqrt{2}\pi \int_0^{\lambda}{\frac{\sqrt{r-s}+\sqrt{r+s}}{\sqrt{r^2-s^2}\sqrt{\sqrt{r^2-s^2}+1-r}}\mathrm{d}s} \\ \stackrel{(5)}{=}&4\pi \sqrt{2r}\int_0^{X}{\frac{1}{\left( t^2+1 \right) \sqrt{\left( 1-2r \right) t^2+1}}\mathrm{d}t} \\ \stackrel{(6)}{=}&4\pi \int_0^{\tan \left( X \right)}{\frac{\sqrt{2r}\cos \left( \theta \right)}{\sqrt{1-2r\sin ^2\left( \theta \right)}}\mathrm{d}\theta} \\ =&4\pi \mathrm{arcsin} \left( \sqrt{2r}\sin \left( \tan \left( X \right) \right) \right) \\ =&4\pi \mathrm{arcsin} \left( \sqrt{r-\sqrt{r^2-\lambda ^2}} \right) \end{align*} (1) $x=\cos \left( \theta \right)$
(2) $\tan \left( \frac{\theta}{2} \right) =t$
(3) $t\rightsquigarrow \frac{1}{t}$
(4) Use the lemma
(5) $s=\frac{2rt}{1+t^2}$
(6) $t=\tan \left( \theta \right)$
(7) $X=\frac{r-\sqrt{r^2-\lambda ^2}}{\lambda}$

---

So, for this question, we have $r=1.5, s=1$, plug the value in, we got $$ \int_{-1}^1{\frac{1}{x}\sqrt{\frac{1+x}{1-x}}\ln \left( \frac{2x^2+2x+1}{2x^2-2x+1} \right)}\mathrm{d}x=4\pi \mathrm{arcsin} \left( \sqrt{\frac{3-\sqrt{5}}{2}} \right) =4\pi \mathrm{arccot} \left( \sqrt{\frac{1+\sqrt{5}}{2}} \right) $$