The problem is as the title suggests, in the figure given below, solve for the missing angle labeled "?". This problem is from my friend @geometri_hayattir on Instagram.
I have solved the problem, and I will share my approach as an answer below. Since the solution of this problem was not posted, I'm unsure if my approach and answer are correct. Please let me know if there are any issues in my method, and please share your own answers and approaches!
This is my approach:
1.) Locate point $E$ outside of $\triangle ABC$ and join it via $AE$ and $CE$ such that $\angle EAC=\angle DAC=30^\circ$ and $AE=AD$. Notice that this means $\triangle AEC$ and $\triangle ADC$ are congruent via the SAS property. [See "motivation" at the end of the answer if you wish to know the motivation behind this particular construction].
2.) Notice that $\triangle AED$ is an equilateral triangle. Also notice that $\angle AEC=\angle ABC=130^\circ$. This implies that Quadrilateral $ACEB$ is a cyclic quadrilateral. Therefore, $\angle AEB=\angle ACB=10^\circ$ and $\angle BAE=\angle BCE=10^\circ$. This implies that $AB=BE$ and $\angle DAB=\angle DEB=70^\circ$. This proves that $\triangle DAB$ is congruent to $\triangle DEB$, therefore $\angle ADB=\angle EDB=30^\circ$. Therefore the missing angle is $60^\circ$.
[Motivation for (1): The motivation behind this construction is very simple, notice that $\angle ADC=\angle ABC=130^\circ$, so by "flipping" $\triangle ADC$ to a congruent triangle $\triangle AEC$ means that we can obtain a cyclic quadrilateral, which from where we can easily exploit the properties of the cyclic quadrilateral to obtain some angles]
I think this solution is simpler:
Mark intersection of AC and BD as E. Draw line ($l_1$) from C parallel with AD. Draw a perpendicular from E on this line and mark their intersection as F, so $\angle BCF=30^o$.Draw line(l_2) from C which has angle $10^o$ with CD,so $\angle ACG=30^o$. Draw a perpendicular from F on AC , mark it's foot on AC as H; extend it to meet line $l_2$ at G, . In this way quadrilateral EGCF is symmetric about AC. In right angled triangle FHC $\angle HFC=60^o$, therefore in right angled triangle EFH $\angle FEH=60^o$. Since the figure is symmetric about Ac the $\angle DFC=\angle FEH=60^o$.
Here is one more solution showing how such problems are constructed. We realize the given situation in the context of a regular polygon, well the nature of the angles require a regular $18$-gon. Denote its vertices by $0,1,2,3,4,5,6,7,8,9,8',7',6',5',4',3',2',1'$ in this cyclic order. Place $A,B,C$ in $0,1,5$, so $\Delta ABC$ matches the one from the problem. Where is $D$ now?
Take $D$ to be the orthoceter of $\Delta 056'=\Delta AB6'$. Since $08\perp 56'$, and $52'\perp 06'$, and $6'2\perp 05$ we see that $$ \color{blue} { D=08\cap 52'\cap 6'2 } \color{green} { \cap 18' } \color{brown} { \cap 43' } \ . $$ The blue lines correspond to the heights. The green line is the diameter $18'$, the axis of symmetry for $ \color{blue} { 08\cap 26' } $. And having this symmetry, we can add the brown line, too, (although not needed in the sequel,) since $52'$ and $43'$ are mirrored.
We have constructed the quadrilateral $ABCD$ from the problem in a setting that allows to write immediately the angle between its diagonals that meet in $E$, say: $$ \bbox[yellow]{\color{blue} { \widehat{AEB} =\frac 12\left(\ \overset\frown {AB} +\overset\frown {58'} \ \right) =\frac 12\left(\ 20^\circ+100^\circ \ \right) =60^\circ\ . }} $$ $\square$
Later EDIT: From the comments, there is some interest in problems with solutions of the same shape. Generally, this approach realizes a given situation with angles (and maybe also metric relations) in a structure that it is directly related to a regular polygon. Then it transforms the "find the angle task" equivalently in a geometrical property like concurrence (for instance in our case we have five chords concurrent is the point $D$) or colinearity. Then the solution usually uses the bright symmetry of the regular polygon.
Some words on the way to realize a given situation. Points from the problem are usually taken to be vertices of a regular polygon, one of them may be the center, some of them may be specific intersections of diagonals. Here are some problems solved in this manner, unfortunately most of them done by my hand.
This may be already too much to digest, sorry for the bombardment. Just pick one pic from the many links, and dive in on your own! Good luck!
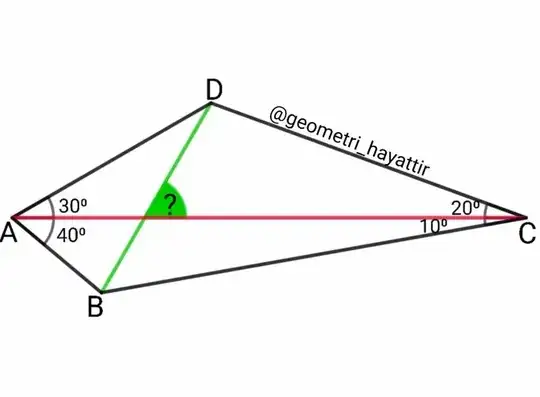
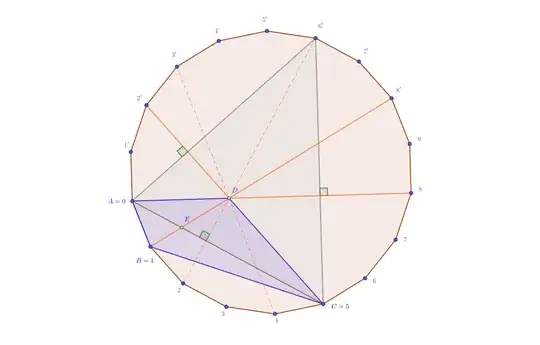
All following angles are measured in degrees.
Let $r>0$.
Construct two circles $\Gamma_1$ and $\Gamma_2$ with respective centers $O_1$, $O_2$ and same radius $r$.
Taking suitable coordinates we may assume that $O_1(t\mathbin;0)$ and $O_2(-t\mathbin;0)$, with $t\in\mathopen]0\mathbin;r\mathclose[$, so that the circles meet at two distinct points $A(-s\mathbin;0)$ and $C(s\mathbin;0)$.
By Pythagoras' theorem $r^2=s^2+t^2$.
From now on we'll even take $0<t<r\frac{\sqrt3}2$ (equivalently $\frac r2<s<r$); this implies that $s>\frac{t}{\sqrt3}\cdot$
Construct a straight line $\Delta$ passing through $O_1$ and making an angle of $60^\circ$ with the line $(AC)$.
This line cuts $\Gamma_1$ at $B$, interior to $\Gamma_2$, and cuts $\Gamma_2$ at $D$, interior to $\Gamma_1$ (which is made possible thanks to the restriction on $t$).
We also name $\Omega$ the intersection between $\Delta$ and $[A\mathbin,C]$.
Taking $y=x\sqrt3+t$ as cartesian equation for $\Delta$, several coordinates can be deduced, as shown on the following picture.
Also, some interesting relations between angles can be computed.
• $\bbox[black,6px]{\color{white}{\alpha=\varphi_2}}$. We have $\overrightarrow{D\Omega}\mathord: \Big(t\frac{\sqrt3}6-\frac s2\mathbin;\frac t2-s\frac{\sqrt3}2\Big)$, thus $D\Omega=\frac{t^2}3+s^2-2ts\frac{\sqrt3}3 =\Big(s-\frac t{\sqrt3}\Big)^2$; this gives $D\Omega=s-\frac t{\sqrt3}=A\Omega$ and proves that $A\Omega D$ is isosceles, with vertex $\Omega$, and that $\alpha=\varphi_2=30^\circ$.
• $\bbox[black,6px]{\color{white}{\gamma=2\delta}}$.
We have $\overrightarrow{CD}\mathord:
\Big(-t\frac{\sqrt3}2-\frac s2\mathbin;-\frac t2+s\frac{\sqrt3}2\Big)$, which provides $CD=\sqrt{s^2+t^2}=r$.
We compute $\overrightarrow{CA}.\overrightarrow{CD}=s(s+t\sqrt3)$.
Then $\cos\gamma=\frac{\overrightarrow{CA}.\overrightarrow{CD}}{CA.CD}
=\frac{s+t\sqrt3}{2r}\cdot$
Then we can compute $\cos\delta=\frac{r+2s}{2\sqrt{r(2r+s-t\sqrt3)}}$ and deduce from it that
$$\begin{array}{rcl}
2\cos^2\delta-1&=&\frac{(r+2s)^2-2r(2r+s-t\sqrt3)}{2r(2r+s-t\sqrt3)}\\[3pt]
&\vdots&\\
&=&\frac{s+t\sqrt3}{2r}
=\cos\gamma.
\end{array}$$
That is: $\cos(2\delta)=\cos\gamma$.
Using the fact that the sum of interior angles of a triangle is $180$, we deduce:
$\vartheta_2=120-\gamma=120-2\delta=2(60-\delta)=2\vartheta_1$.
• $\bbox[black,6px]{\color{white}{\vartheta_1=90-\beta}}$.
$\cos\vartheta_1=\frac{\overrightarrow{BC}.\overrightarrow{BD}}{BC.BD}$ can be computed as above.
We use $BD=r+s-t\sqrt3$, $BC=\sqrt{r(2r+s-t\sqrt3)}$,
$\overrightarrow{BC}.\overrightarrow{BD}
=\frac12(r+s-t\sqrt3)(2r+s-t\sqrt3)$
and obtain $\cos\vartheta_1=\frac12\sqrt{\frac{2r+s-t\sqrt3}{r}}\cdot$
Similarly (details omitted) we get $\cos\beta =\frac{s-\frac r2}{\sqrt{r(2r+s-t\sqrt3)}}\cdot$
Finally we obtain $\cos^2\vartheta_1+\cos^2\beta=1$. This shows that $\vartheta_1+\beta=90$.
• Back to the initial question.
Taking $t=r\cos50^\circ$, we get $\cos\gamma=\frac{s+t\sqrt3}{2r}
=\sin50^\circ\sin30^\circ+\cos50^\circ\cos30^\circ
=\cos20^\circ$.
This gives $\gamma=20^\circ$, $\delta=10^\circ$, then $\vartheta_2=100^\circ$, $\vartheta_1=50^\circ$ and $\beta=40^\circ$.
• Another instance with a different choice for $t$:
• Comment.
Experimenting with Geogebra seems to indicate that, if one chooses another initial angle than $60^\circ$, then the relation $\beta+\vartheta_1=90$ stills holds…
