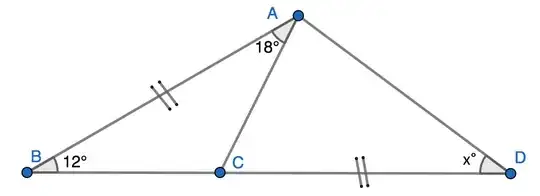
I will insert a slow geometric solution. Doing it in steps may allow a pause after any step, the ambitious reader may want to find her or his own path to the solution. This may be also a good preparation for an olympiad or related challenge... The reader in hurry may chose to consume one of the two solutions listed in (4) and/or (5), which can be understood independently.
(1) Some picture:
In such situations it may be useful to use the pattern of an existing symmetry inside a regular polygon. The given triangle $\Delta ABC$ should be realized with vertices among the vertices of the polygon. (But the imagination of the solver should not stop here, sometimes using the center or some related intersection of diagonals may be also fruitful.) In our case we search a constellation with $A,B,C$ among the vertices of the regular polygon $P_{30}$.
If the vertices are $0,1,2,3,\dots,14, 15=-15, 16=-14,\dots, 29=-1$, denoted using the elements of $\Bbb Z/30$, then a possible choice is $B=0$, $C=3$, $A=5$.
We draw first a circle $(O)$ centered in some point $O$.
Since the angles with measures $12^\circ$ and $18^\circ$ are given, we expect to "see" also an inscribed angle in $(O)$ with measure $6^\circ$, so we decide to draw a $30$-gon inscribed in $(O)$. We fix the position of $A$, make then the one or the other choice of the position of $B$ and obtain the following picture:
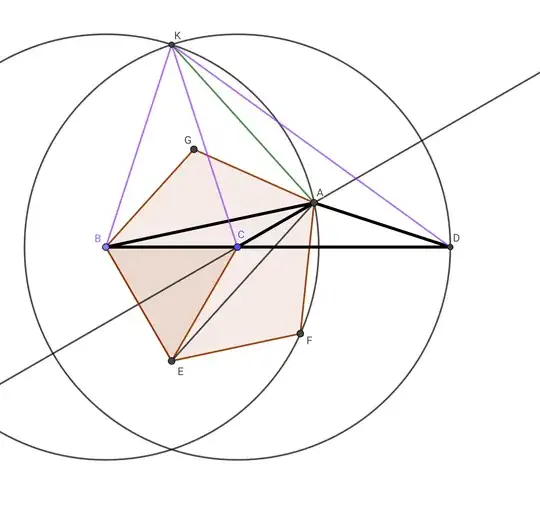
In the figure, we have also constructed the point $D$ as follows.
Let $(A)$ be the circle centered in $A$ with radius $AB$. Let $S,T$ be the two points of intersection of $(A)$ with the parallel trough $A$ to $BC$. Here $S$ is the point making $\Delta ABS$ to have angles $<90^\circ$, so the angles are $12^\circ$ in $A$, and $84^\circ$ in $B$ and $S$.
The triangle $\Delta ABT$ has an angle with measure $180^\circ-12^\circ$ in $A$, and two $6^\circ$ angles in $B$ and $T$. Then $D$ is determined by constructing the parallelogram $TACD$.
Note that the circle $(A)$ passes through $O$.
We draw $DA$ and ask for the angle between the lines $AD$ and $BCD$. The picture suggests the next step, try to pause consuming the solution at this point...
(2) Some more observations and another picture:
In the regular polygon $P_{30}$ recall that the vertices are indexed via $\Bbb Z/30$. Then $BA=05$ or in general a segment $[k,k+5]$ is the side of a regular hexagon inscribed in $(O)$. So $BA$ is also equal to the radius $OA=OB$ in $(O)$. The OP mentions the need to find an equilateral triangle, well, here is one...
We consider closer the relation of the circles centered in $O,A,C$ having as radius this distance
$$
OA=OB=AB=AS=AT=CD=CO\ .
$$
Consider also the regular congruent $30$-gons on the circles $(O)$, $(A)$, $(C)$. (Note that main diagonals in the one or the other $30$-gon pass through vertices of the other $30$-gons, angle argument.)
Observation: We obtain the $30$-gon inside $(C)$ from the $30$-gon inside $(A)$ by a translation with the vector $\vec{AC}=\vec{TD}$.
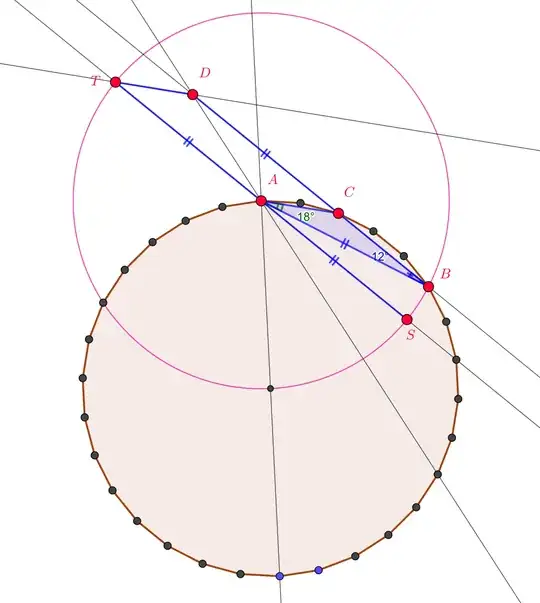
This picture is of course too much and not needed, for the OP we want to know the angles in the paralellogram $ACDT$ formed by the diagonal $DA$ with the sides.
Let $U$ be the point with $\vec{AC}=\vec{SU}$. The parallelograms $TDCA$ and $ACUS$ are congruent.
(3) An other observation and yet an other picture:
In (2) the way to reason was as follows. The circles $(A)$ and $(C)$ have the same radius, thus they are congruent. Consider the vector $\vec{AC}$, it translates $(A)$ into $(C)$, and in particular also a specific $30$-gon inscribed in $A$ into a specific $30$-gon inscribed in $(C)$ if we insure that (at least) one vertex of the first $30$-gon goes to one vertex of the other $30$-gon.
The same applies also with the pair of circles $(A)$ and $(O)$, and/or with the pair of circles $(C)$ and $(O)$ correspondingly instead.
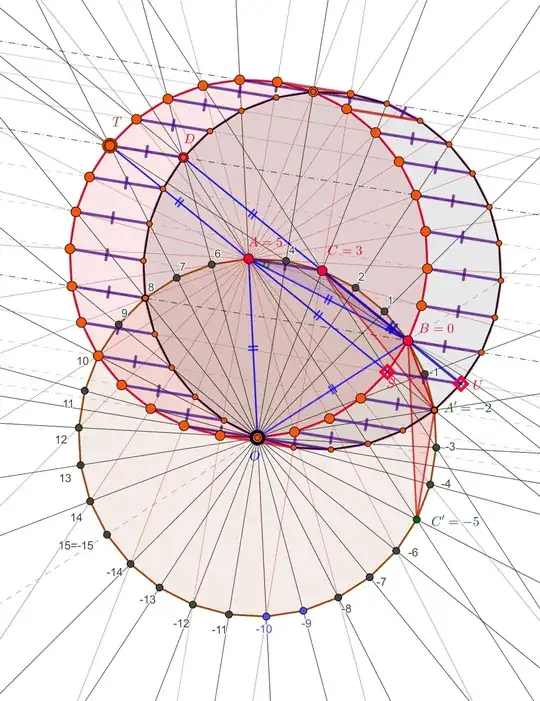
A similar observation can be done with rotations (instead of translations). For example... The circles $(A)$ and $C$ are passing through $O$ (and an other point). Consider the rotation centered in $O$ which maps $A$ into $C$. Then it maps the $30$-gon inscribed in $A$ with one vertex in $O$ into the $30$-gon inscribed in $C$ with one vertex in $O$. A picture suggesting the movement of the vertices by drawn circles of guidance would be:
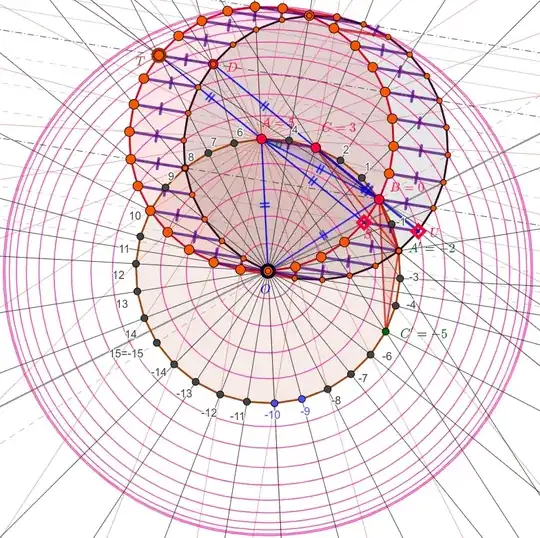
Again, this is too much for our purposes, but we are only collecting ideas.
When searching for a solution, the idea is to use some pointed points under the many points constructed above.
(4) Solution I:
- Let $O$ be a point and $(O)$ a circle centered in $O$ with radius $R$. Let $O(30)$ denote a fixed $30$-gon inscribed in $(O)$, its vertices are denoted by $0,1,2,\dots\in\Bbb Z/30$, and for some points we use alternative notations.
- The first three points we want to evidentiate are $B=0$, $C=3$, and $A=5$.
- Let $(A)$ and $(C)$ be the circles centered in $A$, respectively $C$ passing through $O$. They also have radius $R$. We draw the $30$-gons $A(30)$, and respectively $C(30)$ inscribed in these two circles having $O$ as one vertex in common, and denote the vertices in them by
$A_0$, $A_1$, $A_2$, and so on,
respectively
$C_0$, $C_1$, $C_2$, and so on. The indices are also living in $\Bbb /30$.
- The starting point when counting is $O$, so $(A)$ and $(C)$ intersect in $O=A_0=C_0$, and in $A_{13}=C_{-13}$.
- $\Delta ABO$ is equilateral, its sides are $R$.
- We thus know the angle $\widehat{OBC}=60^\circ+12^\circ$, so $BC$ intersects $(C)$ for the second time in $D=C_{-9}$.
- The radius $AB$ sits on the diameter $A_5A_{-10}$. We know the angle $\widehat{ABC}=12^\circ$, so $BC$ intersects for the second time $(A)$ in $A_{-12}$.
- Similar knowledge of angles shows that the parallel through $A$ to the line $BCDA_{-12}$ is the line $TC_{-8}AA_4C_5$.
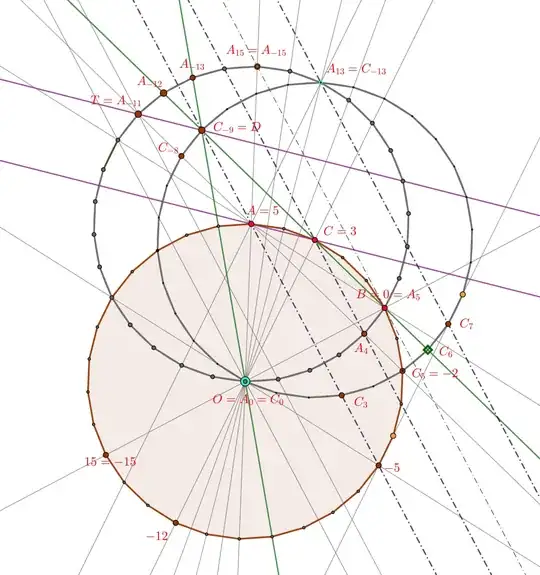
- Now start the solution, and show the equality of lines $(5,-5)$ and $C_3C_{-9}$. In $(O)$, the line between $5$ and $-5$ is the perpendicular bisector of the radius $O0=OB$, as a visual help consider the equilateral triangles $\Delta OB5=\Delta OBA$ and $\Delta OB-5$. The translation of the plane with vector $\vec{OC}$ transforms circles $(O)\to(C)$, and regular polygons $O(30)\to C(30)$. The chord $(5, -5)$ is mapped to the chord $C_{-13}C_7$. Note also that the perpendicular in $0=A_5$ to $(O)$ has known angle w.r.t. $AB=AA_5$, wo we can identify the direction perpendicular to $OB$ also in the circle $(A)$, it is $A_5A_{15}$. From this we obtain a parallelism
$$(5,-5)\| C_{-13}C_7\|C_{-13+4}C_{7-4}=C_{-9}C_3\|\dots
\\
\dots\| A_5A_{-15}\|A_4A_{-14}\|A_3A_{-13}\|A_2A_{-12}\|A_1A_{-11}\|OA_{-10}\ .$$
The diameter through $C_{-9}=D$ in $C$ is $C_{-9}C_6$. Reflecting the line
$$
(l) =C_{-9}CC_6=DCB=\color{blue}{A_{-12}A_5}
$$
w.r.t. to the line $\color{red}{C_{-9}C_3}$ gives the line
$$
(l')=C_{-9}C_{3-3}=DO=D\color{blue}{A_0}\ .
$$
And yes, there is exactly one isosceles trapez $\color{blue}{A_{-12}A_0A_5A_?}$ which is symmetric w.r.t. a direction matching the above parallelism, it is
$\color{blue}{A_{-12}A_0A_5A_{-13}}$, and its symmetry axis passes through the center $A$ of the circle $(A)$. So the parallel lines
$\color{red}{C_{-9}C_3}$ and $\color{red}{-5\;A}$ both contain $A$, so they are equal. This shows the colinearity of the points
$$
D=C_{-9}\ ,\ A=5\ ,\ C_3\ ,\ -5\ .
$$
The needed angle is for instance half of the angle between the diagonals of the above trapez, so it is
$$
\widehat{ADB}
=\frac 12\widehat{ODB}
=\frac14(\overset\frown{A_{-12}A_{-13}} + \overset\frown{A_0A_5})
=\frac14(1\cdot 12^\circ + 5\cdot 12^\circ )
=18^\circ\ .
$$
$\square$
(5) Solution II:
We use the same notations as above, else this would make 60% of the solution.
Using the rotation $\mathcal R$ centered in $O$ that maps $C=3$ to $A=5$ we can ask for the angle in $A_{-9}$ in $\Delta A_{-9}57=\mathcal R\Delta C_{-9}35$ instead of the angle in $A_{-9}$ in $\Delta C_{-9}35=\Delta DCA$ asked in the OP, and thus we completely remove from the picture $(C)$ and $C(30)$.
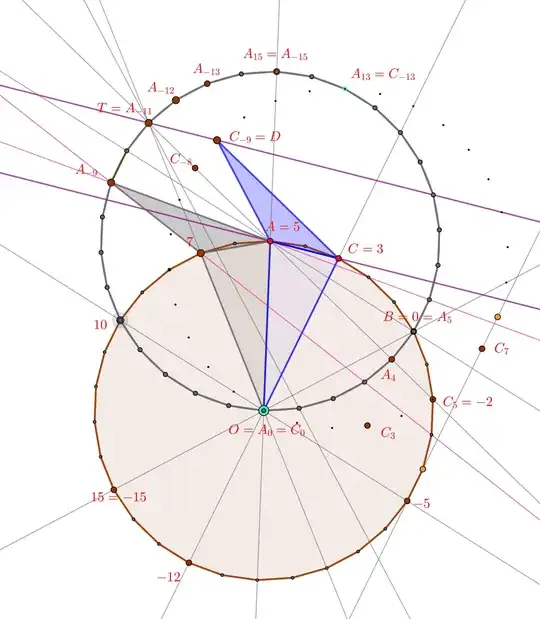
We know the angle
$\widehat{A_{-9}AO}
=\widehat{C_{-9}CO}$, or use the colinearity $(A_{-9}52)=\mathcal R(C_{-9}30)$, to obtain that $A_{-9}52A_6$ is a line (supported on the diameter $A_{-9}A_6$.
The angles between the one fixed line $O,10$ and $OA_{-9}$ and $O8$ are equal, so $O, 8,A_{-9}$ are colinear. The two angles
- between the chords $8,O,-7$ and $7,-3$ in $(O)$
- between $A_{-9}A_0$ and $A_{-9}A_3$ in $(A)$
are equal, $4-1=3$, and two of the above chords are on the same line, so we obtain the colinearity of points
$$
A_{-9},\ A_3\ ,\ 7\ ,\ -3\ .
$$
The needed angle is thus
$$
\widehat{CDA} =
\widehat{3C_{-9}5} \overset{\mathcal R}=
\widehat{5A_{-9}7} =
\widehat{A_6A_{-9}A_3} =
\frac 12\overset\frown{A_6A_3}
=\frac 12\cdot3\cdot 12^\circ
=18^\circ
\ .
$$
$\square$