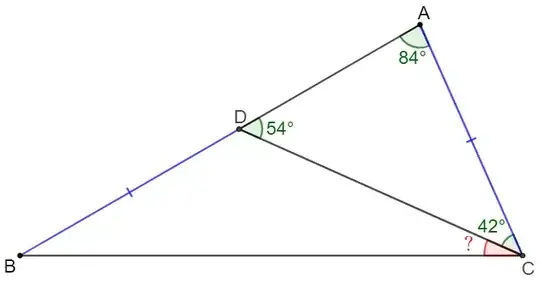
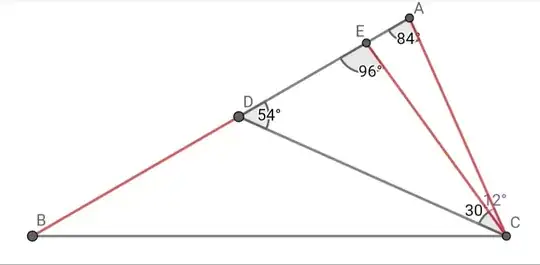
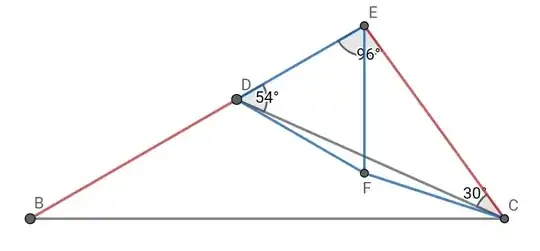
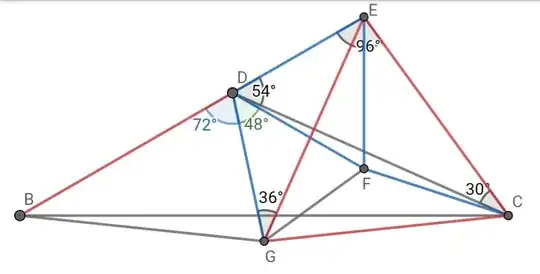
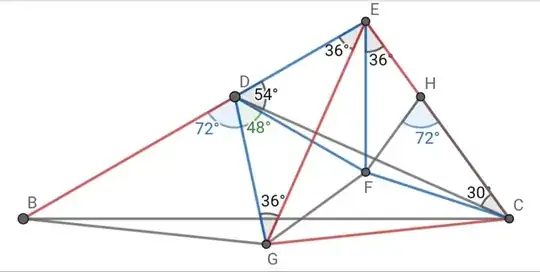
Where $\angle{A}=84^{\circ}, \angle{ACD}=42^{\circ}, BD=AC$, find $\angle{BCD}$.
Wonder if there is solution without using trigonometric functions.
I tried with getting circumcenter of triangle ABC, but seems hard to prove it forms an equilateral triangle with side AC.
Also if trying from equilateral and form an Isosceles triangle with two angles of $24^{\circ}$, and then form another isosceles triangle with top angle to be $\angle{B}=24^{\circ}$, it is not easy to prove that $\angle{ADC}=54^{\circ}$.