0

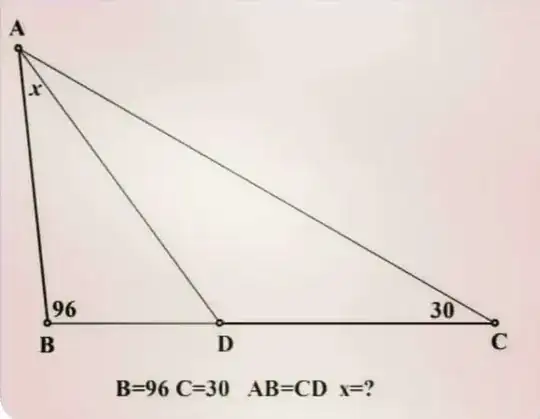
As title suggests, the goal is to solve for angle measure of $x$ in the given triangle $\triangle ABC$ with some angles and two equal sides given. This is a fairly unique problem and I'm curious to see what other ways there could be of solving this, so please comment your own answers as well! I'll post my own approach as well.

enter image description here

冥王 Hades
  • 3,083

3 Answers3

4

This is my own approach. I'll add a brief explanation too:

enter image description here

This is the procedure I followed:

1.) Label the triangle $ABC$ and mark all the appropriate angles and side lengths. Notice that since $\triangle ABC$ is obtuse, its circumcenter must lie outside of the triangle itself. Locate circumcenter of $\triangle ABC$ outside and call it point $E$. Connect all the vertices of $\triangle ABC$ to $E$ via $AE$, $BE$ and $CE$. Notice that this means $AB=BE=AE=CE=CD$ because $\triangle ABE$ is equilateral.

(for further explanation of above, point $E$ is a circumcenter of $\triangle ABC$, in that case, $\angle AEB$ must be twice the measure of $\angle ACB$ (inscribed angle theorem), which means it'll be $60$. Because $\angle AEB=60$ and know that $AE=BE$, it follows that $\triangle ABE$ is equilateral)

2.) Notice also that $\angle EAC=\angle ECA=6$. Connect point $D$ with $E$ via segment $DE$. Notice that because segment $CD=CE$ and $\angle ECD=36$, this implies that $\angle EDC=\angle DEC=72$. However, notice that $\angle EBD=96-60=36$, therefore, $\angle BED$ is also $36$. But this implies that segment $BD=DE$

3.) Lastly, notice that this means $\triangle ABD$ is congruent to $\triangle AED$ via the SAS property. This means $\angle BAD=\angle EAD=x$. This means that $2x=60$, therefore, $x=30$.

冥王 Hades
  • 3,083
  • 2
    Whys is this not part of the question? – Andrei Oct 07 '22 at 13:42
  • I noticed that if I posted the answer within the question space, it looks pretty cluttered, so I decide to post it separately – 冥王 Hades Oct 07 '22 at 13:43
  • 1
    The only thing not clear is in the first step. I know that $AE=BE$, but why is it also equal to $AB$? Why is $\triangle ABE$ equilateral and not just isosceles? – Andrei Oct 07 '22 at 13:52
  • 1
    @Andrei This is due to the fact, as I specified, that point $E$ is a circumcenter of $\triangle ABC$, in that case, $\angle AEB$ must be twice the measure of $\angle ACB$ (inscribed angle theorem), which means it'll be $60$. Because $\angle AEB=60$ and know that $AE=BE$, it follows that $\triangle ABE$ is equilateral, therefore, $AE=BE=AB$ – 冥王 Hades Oct 07 '22 at 13:55
  • 1
    Nice answer. I would add the above explanation to it. – Andrei Oct 07 '22 at 13:57
  • Why $\angle EAC=\angle ECA=6$? – ACB Nov 20 '22 at 06:24
  • @ACB Are you asking why they're equal or why they're $6°$? – 冥王 Hades Nov 20 '22 at 10:02
  • Obviously they are equal. But it's not clear to me how you deduced they are equal to $6^\circ$ in the second step. – ACB Nov 20 '22 at 18:10
  • 1
    @ACB Alright. That's very easy to deduce, but maybe I shouldn't have glossed over it. So, notice that $E$ is the circumcenter of ∆ABC. This means that $E$ is equidistant from $A, B$ and $C$. In other words, $AE=BE=CE$. Now, because $E$ is the circumcenter, <AEC must be twice of its inscribed angle, and its inscribed angle=180-<ABC=84. Thus <EAC=168, and since $AE=CE$, we know that <EAC+<ECA=180-168, therefore <EAC=6° – 冥王 Hades Nov 20 '22 at 18:45
  • Thanks, it makes sense. Btw, I am not sure why I missed that :P. It can also be derived easily from the fact that triangle BEC is isosceles. And if it helps, here's one of my answers dealing with a similar problem. – ACB Nov 21 '22 at 02:44
1

This is not as nice approach as the other answer. Just use the law of sines: $$\frac{AB}{\sin\angle ADB}=\frac{AD}{\sin\angle ABD}\\\frac{DC}{\sin\angle CAD}=\frac{AD}{\sin\angle ACD}$$ Knowing that $AB=DC$ and $AD$ is common: $$\frac{\sin\angle CAD}{\sin\angle ACD}=\frac{\sin\angle ADB}{\sin \angle ABD}$$ In terms of the numbers and $x$, $$\frac{\sin(54^\circ-x)}{\sin(30^\circ)}=\frac{\sin(84^\circ-x)}{\sin(96^\circ)}$$ After some simple manipulation, using $\sin(a-b)=\sin a\cos b-\cos a\sin b$, then grouping the terms with $\sin x$ and $\cos x$, one gets: $$\frac{\sin 54^\circ\cos x-\cos54^\circ\sin x}{\sin 30^\circ}=\frac{\sin 84^\circ\cos x-\cos84^\circ\sin x}{\sin 96^\circ}\\\cos x\left(\frac{\sin 54^\circ}{\sin 30^\circ}-\frac{\sin 84 ^\circ}{\sin 96^\circ}\right)=\sin x\left(\frac{\cos 54 ^\circ}{\sin30^\circ}-\frac{\cos84^\circ}{\sin 96^\circ}\right)$$ $$\tan x=\frac{\frac{\sin 54^\circ}{\sin 30^\circ}-\frac{\sin84^\circ}{\sin 96^\circ}}{\frac{\cos 54^\circ}{\sin 30^\circ}-\frac{\cos84^\circ}{\sin 96^\circ}}$$ I have plugged the values in a calculator and I get $x=30^\circ$

Andrei
  • 37,370
  • That's a nice trig approach. By the way, on the second last steps where you obtain the trigonometric ratios before making a change to the $tan$ function, could you maybe elaborate on some of the manipulations that you talked about? – 冥王 Hades Oct 07 '22 at 20:51
  • 1
    I've just used $\sin(a-b)=\sin a\cos b-\cos a\sin b$. Then I've grouped together the terms with $\sin x$ and with $\cos x$. I can add this to the answer, if you think is necessary. – Andrei Oct 08 '22 at 01:46
  • Please do add it as a side note. – 冥王 Hades Oct 08 '22 at 01:53
  • 1
    Done. All the missing steps are there. I still like the geometric solution better. I did not try it, but I think I can get the same formula using vector product to write the areas of the triangles. – Andrei Oct 08 '22 at 02:01
  • Funny enough I too have been thinking of a way to use cross products to arrive at the same results. – 冥王 Hades Oct 08 '22 at 02:24
1

Law of Sine on ΔABC

$\displaystyle \frac{AB}{\sin 30°} = \frac{BC}{\sin(180°-96°-30°)}=\frac{AB+BD}{\sin 54°}$

Golden triangles: $\;\sin 54° = \cos 36° = ϕ/2$

$\displaystyle → \frac{AB}{BD} = \frac{1}{ϕ-1} = ϕ$

Law of Sine on ΔABD

$\displaystyle \frac{BD}{\sin x} = \frac{AB}{\sin(180°-96°-x)}$

$\displaystyle \frac{\cos(x+6°)}{\sin x} = ϕ = \frac{ϕ/2}{1/2} = \frac{\cos 36°}{\sin 30°} \quad → x=30°$

To be adventurous ... what if we solve x first, then simplify?

$\displaystyle \frac{(\cos x)(\cos 6°) - (\sin x)(\sin 6°)}{\sin x} = ϕ \quad →\cot x = \frac{ϕ + \sin 6°}{\cos 6°}$

$ ϕ = 2\,\cos(30°+6°) = (\sqrt{3})(\cos6°) - (1)(\sin 6°)$

$→\;\;\; x = \cot^{-1} \sqrt{3} = 30°$

albert chan
  • 2,114