Find $\angle{CAD}$ in equilateral triangle $\triangle{ABC}$ for $D$ inside with $\angle{ABD}=18^{\circ}, \angle{BCD}=12^{\circ}$

Question

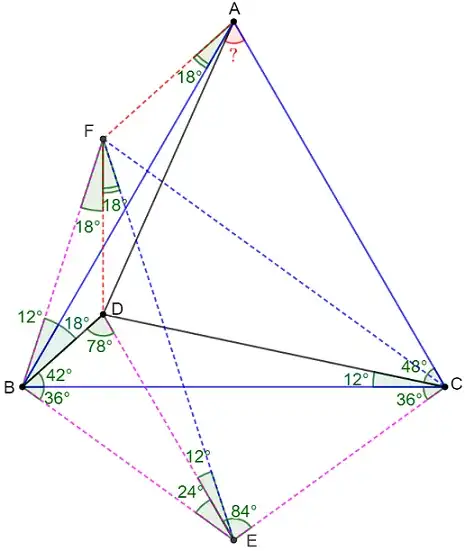
This problem is feasible to solve using trigonometric functions. I am looking for pure geometric solution as usual. Thanks...

Answer 1

Let consider following construction. ABCDE is regular pentagon. ABF is equilateral triangle, F is inside pentagon. G is point inside triangle ABF such that angle GAB is equal 42° and angle GBA is equal 54°. Let connect point F with A, B, C and D, and connect point G with points A, B, C and F. Using the fact that angle of pentagon is equal 108°, one can show that triangles ABG, CBG and CDF are congruent, then triangle CFG is isosceles, then angle CFG is equal 78° Then angle BFG is equal 12°.

ABH is equilateral triangle with H outside pentagon. I is point inside triangle ABH such that angle IHB is equal 42° and angle IBH is equal 54°. Then triangle HBI is congruent to triangle ABG, then BI is equal BG, then triangle ABI is congruent to triangle FBG, then angle BAI is equal 12°. Also angle IBJ is equal 6°, then triangle BIG is equilateral.

Let J is point on AB such that quadrilateral AGIJ is inscribed. Then angle IGJ is equal to angle IAJ and equal 12°. Also angle GIJ is equal angle GAB and equal 42°.

Let consider equilateral triangle A'B'C'. D' is point inside triangle A'B'C' such that angle D'B'C' is equal 42° and angle D'C'B' is equal 12°. Then triangle D'B'A' is similar to triangle JIG by two angles. Then triangle JGB is similar to D'C'A' by two sides and angle. Then angle D'A'C' is equal to angle JBG and equal 54°.

Answer 2

Let $E$ be the circumcenter of $\triangle{BCD}$, so

$BE=CE=DE, \angle{BED}=2\angle{BCD}=2*12^{\circ}=24^{\circ} \\ \implies \angle{EBD}=\angle{BDE}=\dfrac{180^{\circ}-24^{\circ}}{2}=78^{\circ} \\ \implies \angle{EBC}=\angle{ECB}=78^{\circ}-42^{\circ}=36^{\circ} \\ \implies \angle{BEC}=108^{\circ}$

Find $F$ so that $BE=BF=CE=DE, \angle{FBE}=108^{\circ}$, connect $AF, CF, DF, EF$. So

• $\angle{FBC}=108^{\circ}-36^{\circ}=72^{\circ}$

• $\triangle{BCE} \cong \triangle{BEF} \implies EF=BC=AB, \angle{BFE}=\angle{BEF}=36^{\circ}=\angle{BCE}=\angle{EBC} \\ \implies \angle{DEF}=36^{\circ}-24^{\circ}=12^{\circ} $

• $\angle{ABF}=108^{\circ}-78^{\circ}-18^{\circ}=12^{\circ}=\angle{DEF}$

$\implies \triangle{ABF} \cong \triangle{FED} \text{ [SAS]} \\ \implies AF=DF, \angle{FAB}=\angle{DFE} \\ \implies \angle{FDA}=\angle{FAD} \\ \text{Also we have }\angle{BFE}=\angle{BCE} \implies BECF \text{ are cyclic} \\ \implies \angle{FCB}=\angle{BEF}=36^{\circ} \\ \implies \angle{BFC}=180^{\circ}-\angle{FCB}-\angle{FBC}=72^{\circ}=\angle{FBC} \\ \implies BC=FC=AC \\ \implies \text{C is circumcenter of } \triangle{ABF} \\ \implies \angle{AFB}=180^{\circ}-\dfrac{\angle{ACB}}{2}=180^{\circ}-30^{\circ}=150^{\circ} \\ \implies \angle{FAB}=\angle{DFE}=180^{\circ}-150^{\circ}-12^{\circ}=18^{\circ} \\ \implies \angle{BFD}=36^{\circ}-18^{\circ}=18^{\circ} \\ \implies \angle{DFA}=150^{\circ}-18^{\circ}=132^{\circ} \\ \implies \angle{FDA}=\angle{FAD}=\dfrac{180^{\circ}-132^{\circ}}{2}=24^{\circ} \\ \implies \angle{BAD}=\angle{FAD}-\angle{FAB}=24^{\circ}-18^{\circ}=6^{\circ} \\ \implies \angle{DAC}=\angle{BAC}-\angle{BAD}=60^{\circ}-6^{\circ}=\boxed{54^{\circ}}$