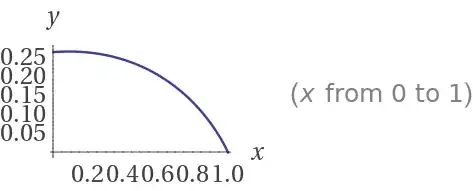Based on:
Conjecture: $$\lim\limits_{x\to\infty}\operatorname{Re}\text W_x(x)\mathop=\limits^?-\ln(2\pi)$$
and
On completing the solution for $$\int_0^1 Q^{-1}(x,x) dx$$ and other constants.
Here is the goal limit again using the central Inverse Regularized Gamma function $Q^{-1}(x,x)$:
$$α\mathop=^\text{def} \lim_{x\to0} Q^{-1}(x,x)=Q^{-1}(0,0)\ne 0$$
Note that Wolfram Alpha says that $Q^{-1}(0,0)=0$, but this is just due to the definition of the function. If you take a look at the graph, the “true” limit clearly is not $0$:
However, we can use the main Taylor series definition centered at $x=1$ with the new $C_{n,x}$ coefficient notation. Note that there are other series in the bolded link.
$$Q^{-1}(x,x)=((1-x)x!)^\frac1x+\frac {((1-x)x!)^\frac2x}{x+1}+ \frac {(3x+5)((1-x)x!)^\frac3x}{2(x+1)^2(x+2)}+O\left((x-1)^\frac4x \right)\mathop =^\text{def}\sum_{n=0}^\infty C_{n,x}\cdot ((1-x)x!)^\frac nx$$
Now let’s apply the limit noting that we can apply the limit term by term. The limit is a long process, but ends up being in terms of $e$ and the Euler-Mascheroni constant γ:
$$α= \lim_{x\to0} Q^{-1}(x,x)=Q^{-1}(0,0)= \lim_{x\to 0}\sum_{n=0}^\infty C_{n,x}\cdot ((1-x)x!)^\frac nx=\sum_{n=1}^\infty \frac{C_{n,0}}{e^{(γ+1)n}} = e^{-(γ+1)}+ e^{-2(γ+1)}+ \frac 54 e^{-3(γ+1)}+\frac{31}{18} e^{-4(γ+1)}+ \frac{361}{144}e^{-5(γ+1)}+\frac{4537}{1200} e^{-6(γ+1)} +…=.26473… $$
A few observations on the constants:
- The nth numerator and denominator of $C_{n,0}$ is on the order of $10^n$ for most of the first few terms.
- Here is a graph of the first few coefficients in the expansion.
An equivalent problem is by solving the following differential equation for the function:
$$y(x)y’’(x)-y’(x)^2(y(x)+1-a)=0,y(x)=Q^{-1}(a,x)\implies y(x)y’’(x)-y’(x)^2(y(x)+1)=0,y(x)=\lim_{a\to 0} Q^{-1}(a,x),y(x)=y(a,x),y(0,0)=α$$
It turns out that the special case can be solved in terms of an Exponential Integral function. Let me “make up” an inverse Exponential Integral function:
$$y(x)y’’(x)-y’(x)^2(y(x)+1)=0\implies c+x=\frac{\text{Ei}(-y(x))}{c}\implies c^2+cx=\text{Ei}(-y(x))\implies y(x)=-\text{Ei}^{-1}(c^2+cx)$$
So the constant is maybe related to Soldner’s Constant
Another idea is letting $x=a$ for:
$$y(x)y’’(x)-y’(x)^2(y(x)+1-a)=0, y(0)$$
but I am not sure if this would produce $y=Q^{-1}(x,x)$.
Amazingly, our differential equation works:
$\text{Ei}(-α)=-1$
Therefore:
$$\text{Ei}(-Q^{-1}(0,0))=\text{Ei}\left(-\sum_\Bbb N C_{n,0} e^{-n(γ+1)}\right)=-1$$
So a “closed form” using a made up Inverse Exponential Integral function would be:
$$α=\lim_{x\to0}Q^{-1}(x,x)=-\text{Ei}^{-1}(-1)$$
You can also find the following assuming an inverse function:
$$y’=ye^y\implies c_1+x=\text{Ei}(-y(x))\implies y(x)=-\text{Ei}^{-1}(x+c_1), x+c_1=-1$$
A better way would be to solve $$\text{Ei}(-x)=-1,x=α$$ for $x$.
Let’s use this method to find many more digits of the constant
$$α=0.264737010451543159461927…$$
while the other real root, for fun, of $\text{Ei}(-x)+1$ is: $$x= -0.1724867417161…$$
Here are $3$ other identities of this constant using this Incomplete Gamma function identity and this Generalized Exponential Integral function. The third one uses the Hyperbolic Cosine and Hyperbolic Sine Integral functions
$$Γ(0,α)=\text E_1(α)=1\implies \int_α^\infty \frac{dx}{xe^x}=1$$
$$\text{Shi}(α)-\text{Chi}(α)=1$$
Note that other constants may also fit the formulas for the constant. Many other identities can be similarly derived, so please go ahead; I have written enough for now. How can I find an alternate form of the constant? Please correct me and give me feedback!