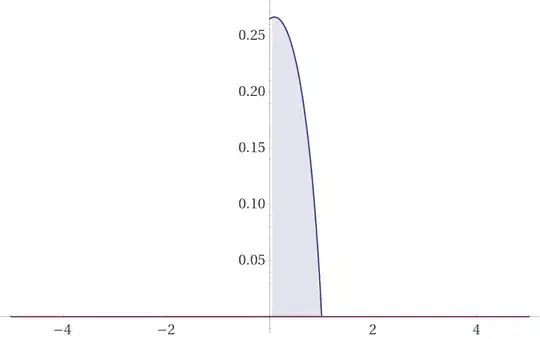
$\frak Q$:
Note this answer needs help from you to find the full solution.
Amazingly there is another identity found based on this similar question about
Finding $\int_0^{.25991…} Q^{-1}(x,x,x) dx$
which shows it can actually solved for. Here are some gamma functions for context.
It actually is possible to integrate $Q^{-1}(x,x)$ many ways, but one way which does not use a general definite integration formula is harder to find. I suspect a closed form is impossible using currently accepted functions. Let’s start with the series representation of $Q^{-1}(x,x)$. This is the notation I will use called $C_{n,x}$ and its definition:
$$Q^{-1}(x,x)=Q^{-1}(x,x,Q(x,x)-x)=((1-x)x!)^\frac1x+\frac {((1-x)x!)^\frac2x}{x+1}+ \frac {(3x+5)((1-x)x!)^\frac3x}{2(x+1)^2(x+2)}+O\left((x-1)^\frac4x \right)= C_{1,x}(1-x)^{1\over x} x!^{1\over x} + C_{2,x}(1-x)^{2 \over x} x!^{2\over x} + C_{3,x}(1-x)^{3 \over x} x!^{3\over x}+…= \sum_{n=1}^\infty C_{n,x}(1-x)^{n \over x} x!^{n\over x} $$
Therefore:$$\int_0^1 Q^{-1}(x,x)dx=\sum_{n=1}^\infty\int_0^1C_{n,x}((1-x)x!)^{\frac nx} dx$$
The next step is to use a Taylor series of $((1-x)x!)^{\frac nx}$ at x=0 which has the amazing form of the following with Apéry’s constant, the Euler-Mascheroni constant, π, and e. Feel free to simplify it as it appears to have a higher degree polynomial with each term. Notice how $\pi$ and ζ($3$) also exhibit this polynomial behavior with each increasing m:
$$\sum_{m=0}^\infty\frac{\left[\frac{d^m}{dx^m} ((1-x)x!)^{\frac nx}\right]_{x=0}x^m}{m!}= e^{-(1 + γ ) n}\left[1 + \frac{π^2 - 6} {12} n x +\frac { nx^2 ((π^2 - 6)^2 n - 96 (ζ(3) +1)) } {288} + \frac{n x^3 (5 (π^2 - 6)^3 n^2 -1440 (π^2 - 6) n (ζ(3) +1)+ 144 (π^4 - 90))}{51840} +\frac{ n x^4 (5 (π^2 - 6)^4 n^3 -2880 (π^2 - 6)^2 n^2 (ζ(3) +1) + 576 n (-90 π^2 - 6 π^4 + π^6 + 60 (13 +8ζ(3) + 4ζ^2(3))) -497664 (ζ(5) ))}{2488320} + O(x^5)\right]
$$
This series converges to $((1-x)x!)^{\frac nx},0\le x\le 1$, so here is the constant so far:
$$\int_0^1 Q^{-1}(x,x)dx= \sum_{n=1}^\infty\int_0^1C_{n,x} \sum_{m=0}^\infty\frac{\left[\frac{d^m}{dx^m} ((1-x)x!)^{\frac nx}\right]_{x=0}x^m}{m!} dx = \sum_{n=1}^\infty\sum_{m=0}^\infty\frac{\left[\frac{d^m}{dx^m} ((1-x)x!)^{\frac nx}\right]_{x=0}}{m!} \int_0^1 C_{n,x} x^m dx$$
Here is where I need to find an expression for $C_{n,x}$. I already know the first few terms using this generalized power series. Here is the constant which should hopefully converge using the n=1,2,3 cases of $C_{n,x}$. Note I used Wolfram Functions and Wolfram Alpha to evaluate and simplify. Note that $H_y$ are the Harmonic numbers and Ф(a,b,c) is the Lerch Transcendent/Zeta function.
Note that I could have integrated up to 4 or more terms, but this becomes tedious and has more interesting complicated functions:
$${\frak Q}=\int_0^1 Q^{-1}(x,x)dx=\int_0^1 P^{-1}(x,x)=\int_0^1 Q^{-1}(x,x,Q(x,x)-x)dx=\int \sum_{m=0}^\infty\frac{\left[\frac{d^m}{dx^m} ((1-x)x!)^{\frac 1x}\right]_{x=0}}{m!} \int_0^1 x^m +\sum_{m=0}^\infty\frac{\left[\frac{d^m}{dx^m} ((1-x)x!)^{\frac 2x}\right]_{x=0}}{m!} \int_0^1\frac{1}{x+1} x^m +\sum_{m=0}^\infty\frac{\left[\frac{d^m}{dx^m} ((1-x)x!)^{\frac 3x}\right]_{x=0}}{m!} \int_0^1\frac {(3x+5)}{2(x+1)^2(x+2)} x^m + \sum_{m=0}^\infty\frac{\left[\frac{d^m}{dx^m} ((1-x)x!)^{\frac 4x}\right]_{x=0}}{m!} \int_0^1\frac{8x^2+33x+31}{3(x+1)^3(x+2)(x+3)}x^m+…=\sum_{m=0}^\infty\frac{\left[\frac{d^m}{dx^m} ((1-x)x!)^{\frac 1x}\right]_{x=0}}{(m+1)!} +\frac12 \sum_{m=0}^\infty\frac{\left[\frac{d^m}{dx^m} ((1-x)x!)^{\frac 2x}\right]_{x=0}}{m!} \left(H_\frac m2-H_\frac{m-1}{2}\right)+ \frac14 \sum_{m=0}^\infty\frac{\left[\frac{d^m}{dx^m} ((1-x)x!)^{\frac 3x}\right]_{x=0}}{m!}\left((2 m - 1) H_\frac m2 - (2 m - 1) H_\frac{m -1}2 -Ф\left(-\frac 12,1,m+1\right)+2\right)+…= \sum_{m=0}^\infty\frac{\left[\frac{d^m}{dx^m} ((1-x)x!)^{\frac 1x}\right]_{x=0}+ \left[\frac{d^m}{dx^m} ((1-x)x!)^{\frac 2x}\right]_{x=0}+ \left[\frac{d^m}{dx^m} ((1-x)x!)^{\frac 3x}\right]_{x=0}+…}{m!} \left[ \frac{1}{m+1}+\frac12 \left(H_\frac m2-H_\frac{m-1}{2}\right)+ \frac14\left((2 m - 1) H_\frac m2 - (2 m - 1) H_\frac{m -1}2 -Ф\left(-\frac 12,1,m+1\right)+2\right)+…\right]=.1984234858… $$
If this formula works, then what is an explicit form for $C_{n,x}$? An explicit formula for $\sum_{m=0}^\infty\frac{\left[\frac{d^m}{dx^m} ((1-x)x!)^{\frac nx}\right]_{x=0}x^m}{m!}$ is also appreciated as its expansion seems to be a double sum of n and x. Any other simplifications are also appreciated.
This leads to the fact that an amazing approximation for $\frak Q$ is the following and proves the series representation of the constant. Note that the rest of the $n\ge 1$ terms will add on smaller values making the approximation better each time:
$${\frak Q}= .19842…≈ \frac{588 + 24 π^2 + π^4 - 96 ζ(3)}{864 e^{γ+1}}=.19289…$$
Note there may be a typo. I hope this shows you that a general Taylor series is all you need to integrate such problems with inverse gamma type functions. Please correct me and give me feedback!
$\mathcal I$:
The real purpose of this question was to find a convergent interval found by @qifeng618:
$$\mathcal I=\int_0^1 \text I^{-1}_x(x,x)=.45697517...$$
which does graphically converge on $0<x\le 2$ from the question.
The area is the area over the function’s domain for $x\in\Bbb R$ Here is the graph of this function:
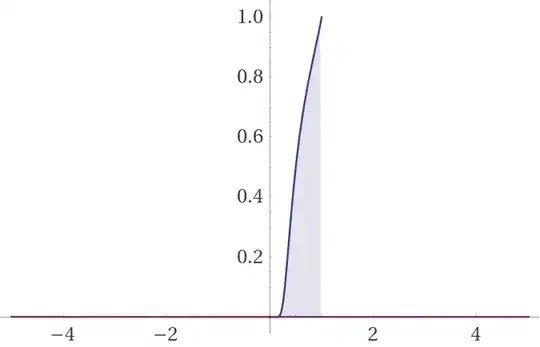
Here is the definition of the function and its properties along with some various beta functions:
$$x=\text I_{I^{-1}_x(y,z)}(y,z)= \text I_{\text I^{-1}_x(x,x)}(x,x)=\frac{\int_0^{\text I^{-1}_x(x,x)}\left(t-t^2\right)^{x-1}dt}{\text B(x,x)}\implies x \text B(x)= \text B_{\text I^{-1}_x(x,x)}(x,x)= \int_0^{\text I^{-1}_x(x,x)}\left(t-t^2\right)^{x-1}dt$$
See this link to derive more results from the definition of the function. I did find this possible form.
Let’s actually begin solving the integral with this series expansion for the Inverse of the Regularized Incomplete Beta function. See the question where @qifeng618 answers well for the first term approximation. Here appears the definition of our $B_{n,x}$ coefficients unrelated to other functions:
$$\text I^{-1}_x(x,x)\mathop=^{x>0}(x^2 \text B(x,x))^\frac 1 x+\frac{x-1}{x+1}(x^2 \text B(x,x))^\frac2x+\frac{2(x-1)(x^2+x-1)}{(x+1)^2(x+2)} (x^2 \text B(x,x))^\frac 3 x+…=B_{1,x} (x^2 \text B(x,x))^\frac 1 x +B_{2,x} (x^2 \text B(x,x))^\frac 2 x +B_{3,x} (x^2 \text B(x,x))^\frac 1 x +…$$
Therefore:
$$\mathcal I=\int_0^1 \text I^{-1}_x(x,x) =\int_0^1 \sum_{n=0}^\infty B_{n,x} (x^2 \text B(x,x))^\frac n x dx= \int_0^1 \sum_{n=0}^\infty B_{n,x} \frac{x!^\frac{2n}{x}}{Γ(2x)^\frac nx} dx $$
Let’s now use the Taylor series for $x!^\frac{2n}{x}$ at $x=0$ for easier integration. Our choice of integration will have consequences for future steps. I could easily have used a more complex Taylor Series, but it would be too complicated to find a formula for. It would also be impractical. Here is the series converging almost certainly for $0\le x\le 2$:
…
Other constant:
Note we also have $$\int_0^.489 \text{erf}^{-1}(x,x)dx$$ as the Inverse of the Generalized Error function. This will be the place for the other main “constants”.
This is a work in progress for fun