Remarks (2022/04/01): @Erik Satie's proof is simpler than mine.
Sketch of @Erik Satie's proof:
Fact 3: Let $0 < y \le 1 \le x$. Then
$$x^{y^2} \ge 1 + \left(x \cdot \frac{1}{1 - (x - 1)(y - 1)} - 1\right) y.$$
Fact 4: Let $0 < y \le 1 \le x$.
Then
$$y^{x^2} \ge 1 + \left(y \cdot \frac{1}{1 - (x - 1)(y - 1)} - 1\right) x.$$
By Facts 3-4, it suffices to prove that
$$\frac{1}{x}\left[1 + \left(\frac{x}{1 - (x - 1)(y - 1)} - 1\right) y\right]
+ \frac{1}{y}\left[1 + \left(\frac{y}{1 - (x - 1)(y - 1)} - 1\right) x\right] \ge 2$$
or
$$\frac{(2xy - x - y)^2}{(x + y - xy)xy} \ge 0$$
which is true.
$\phantom{2}$
Update: I found a simpler proof.
WLOG, assume that $b \le a$.
If $a, b > 1$ or $a, b < 1$, then $a^{b - 1}\ge 1$ and $b^{a - 1}\ge 1$ and thus $$\sqrt{\frac{a^b}{b}} + \sqrt{\frac{b^a}{a}}\ge 2\sqrt[4]{a^{b-1}b^{a-1}} \ge 2.$$
It remains to prove the case when $0 < b \le 1 \le a$.
Let $a = x^2, b = y^2$. It suffices to prove that, for all $0 < y \le 1 \le x $,
$$\frac{x^{y^2}}{y} + \frac{y^{x^2}}{x} \ge 2.$$
$\phantom{2}$
Fact 1: If $x \ge 1$ and $0 < y \le 1$, then
$$x^{y^2} \ge \frac{1 + x + (x - 1)y^2}{1 + x - (x - 1)y^2}.$$
(Proof: Let $f(x) =
y^2\ln x - \ln \frac{1 + x + (x - 1)y^2}{1 + x - (x - 1)y^2} $. We have
$f'(x) = \frac{(1 - y^4)y^2(x - 1)^2}{x[(1 + x)^2 - (x - 1)^2y^4]}\ge 0$. Also, $f(1) = 0$. Thus, $f(x) \ge 0$ for all $x\ge 1$.)
Fact 2: If $x \ge 1$ and $0 < y \le 1$, then
$$y^{x^2} \ge \frac{1 + y + (y - 1)x^2}{1 + y - (y - 1)x^2}.$$
(The proof is given at the end.)
$\phantom{2}$
Now, using Facts 1-2, it suffices to prove that
$$\frac{1}{y}\cdot \frac{1 + x + (x - 1)y^2}{1 + x - (x - 1)y^2}
+ \frac{1}{x}\cdot \frac{1 + y + (y - 1)x^2}{1 + y - (y - 1)x^2} \ge 2.$$
Let $x = 1 + s$ for $s \ge 0$. After clearing the denominators, it suffices to prove that
$$q_4 s^4 + q_3 s^3 + q_2 s^2 + q_1s + q_0 \ge 0 \tag{1}$$
where
\begin{align*}
q_4 &= (1 - y)(2y^3 + y^2 - 2y + 1), \\
q_3 &= (1 - y)(7y^3 + 3y^2 - 11y + 5), \\
q_2 &= - 6y^4 + 8y^3 + 24y^2 - 32y + 10, \\
q_1 &= -2y^4 + 4y^3 + 16y^2 - 28y + 10, \\
q_0 &= 4(1 - y)^2.
\end{align*}
It is easy to prove that $q_4, q_3, q_2, q_0 \ge 0$.
Also, we have
\begin{align*}
4q_2q_0 - q_1^2 = 4(y^3 + y^2 + 7y + 15)(1 - y)^5 \ge 0.
\end{align*}
Thus, (1) is true.
We are done.
Proof of Fact 2: We only need to prove the case when
$\frac{1 + y + (y - 1)x^2}{1 + y - (y - 1)x^2} > 0$,
i.e. $y > \frac{x^2 - 1}{x^2 + 1}$.
In other words, we only need to prove the case when $\frac{x^2 - 1}{x^2 + 1} < y \le 1$.
Let
$$g(y) = x^2\ln y - \ln \frac{1 + y + (y - 1)x^2}{1 + y - (y - 1)x^2}.$$
We have
$$g'(y) = - \frac{x^2(x^4 - 1)(1 - y)^2}{y[1 + y + (y - 1)x^2]^2}\cdot \frac{1 + y + (y - 1)x^2}{1 + y - (y - 1)x^2} \le 0.$$
Also, $g(1) = 0$.
Thus, $g(y) \ge 0$ for all $y \in (0, 1]$.
We are done.
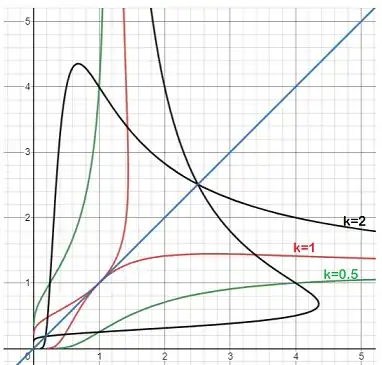
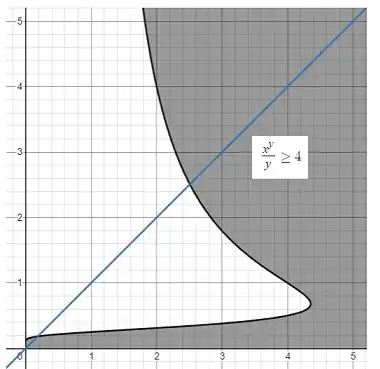
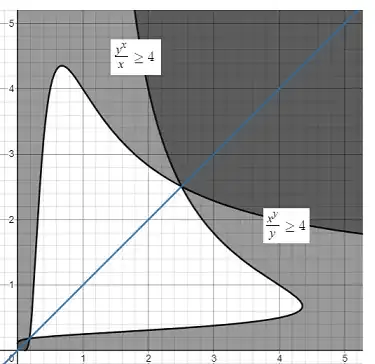


I think the linked question with 84 upvotes is basically where this type of questions started getting attentions.
– dezdichado Oct 14 '21 at 18:08