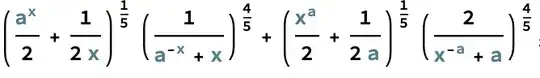About an inequality wich have a link with $\sqrt{\dfrac{a^b}{b}}+\sqrt{\dfrac{b^a}{a}}\ge 2$

Question

Hi it's a follow up of show this inequality $\sqrt{\frac{a^b}{b}}+\sqrt{\frac{b^a}{a}}\ge 2$:

Problem :

Let $a,x>0$ then (dis)prove :

$$\left(\frac{1}{2}a^{x}+\frac{1}{2}x^{-1}\right)^{\frac{1}{5}}\cdot\left(\frac{2}{a^{-x}+x}\right)^{\frac{4}{5}}+\left(\frac{1}{2}x^{a}+\frac{1}{2}a^{-1}\right)^{\frac{1}{5}}\cdot\left(\frac{2}{x^{-a}+a}\right)^{\frac{4}{5}}\geq 2$$

---

---

If true I have tried to show it using the well-know formula :

Let $x$ be a real number then we have :

$$e^x\geq x+1$$

Applying to $a^x$ and $x^a$ .Unfortunately the inequality becomes false .

Also I have tried Tchebytchev's inequality but the application is similar to the use of Am-Gm and the inequality becomes wrong .

I found this refinement as a refinement of Am-Gm-Hm wich is a mix .

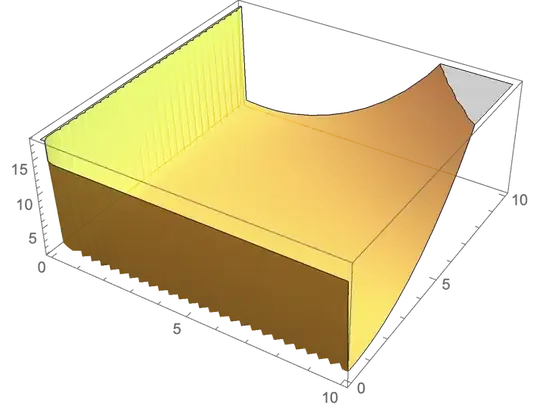
Edit : It seems we have for $a\geq 1$ and $x\in(\frac{1}{a},a)$ :

$$g(x)=\left(\frac{1}{2}a^{x}+\frac{1}{2}x^{-1}\right)^{-\frac{1}{5}}\cdot\left(\frac{2}{a^{-x}+x}\right)^{-\frac{4}{5}}\cdot\left(\frac{1}{2}x^{a}+\frac{1}{2}a^{-1}\right)^{\frac{1}{5}}\cdot\left(\frac{2}{x^{-a}+a}\right)^{\frac{4}{5}}$$

And :

$$h(x)=\left(\frac{1}{2}a+\frac{1}{2}x^{-1}\right)^{-\frac{1}{5}}\cdot\left(\frac{2}{a^{-1}+x}\right)^{-\frac{4}{5}}\cdot\left(\frac{1}{2}x+\frac{1}{2}a^{-1}\right)^{\frac{1}{5}}\cdot\left(\frac{2}{x^{-1}+a}\right)^{\frac{4}{5}}$$

Then it seems we have :

$$h(x)< g(x)$$

Last edit 25/11/2021 correction 26/11/2021:

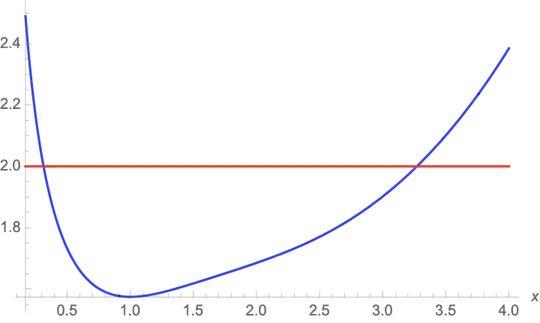
We need to show that for $a\leq 1$ and $x\ge 1$ :

$$2^{\frac{3}{5}}\cdot\frac{\left(\frac{a^{x}}{x}\right)^{\frac{4}{5}}}{\left(a^{x}+\frac{1}{x}\right)^{\frac{3}{5}}}+2^{\frac{3}{5}}\cdot\frac{\left(\frac{x^{a}}{a}\right)^{\frac{4}{5}}}{\left(x^{a}+\frac{1}{a}\right)^{\frac{3}{5}}}\geq 2 $$

Or :

$$x^{-\frac{5}{5}}r\left(a^{x}x\right)+a^{-\frac{5}{5}}r\left(x^{a}a\right)\geq 2$$

Where the function :

$$r\left(x\right)=2^{\frac{3}{5}}\cdot\frac{x^{\frac{4}{5}}}{\left(x+1\right)^{\frac{3}{5}}}$$

Is reciprocally convex on $(0,\infty)$ .

See this paper for further informations : http://artem.sobolev.name/posts/2021-05-02-reciprocal-convexity-to-reverse-the-jensen-inequality.html at ("defined by Merkle")

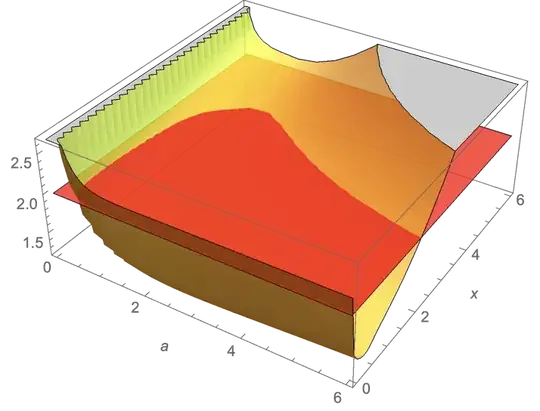
We get a lower bound :

$$\left(\frac{1}{x}+\frac{1}{a}\right)\cdot r\left(\frac{\left(\frac{1}{x}+\frac{1}{a}\right)}{\frac{1}{x}\cdot\frac{1}{\left(a^{x}x\right)}+\frac{1}{a}\left(\frac{1}{x^{a}\cdot a}\right)}\right)$$

It seems to be superior to two when $0.75\leq a\leq 1$ and $0<x\leq 6$

---

---

Question :

How to (dis)prove it ?

Answer 1

Your function looks like this on the reals:

So it is reasonable to expand to small $a$ and $x$ and to examine the curve where the value $2$ is taken. For example $a(x,2)$.

The problem is fundamental because $a^x$ and $x^a$ appear in the composite function. The function is rational and factored in both summands.

Special case is evident $a=x$.

From this visual approach, it is clear together with the fundamentality of the constituents of the composite function that only numerical methods are suitable and understandable to simplify and visualize this inequality.

The result is topping Your work in the very first steps.

An easy path is to approximate around the curve for small values of $a$ and $x$ and for the bigger ones. For small values the curve is for large enough values of the other variable almost a straight line as can be seen in the graph of the function. These approximations are a mathematical art of value to the world.

This is just a motivation to prefer visualization and approximation techniques from numerics and analysis as well as pure analysis.

Nevertheless here some progression:

And viewed from the direction of the surface height.

This is implicit a clear idea where the equality holds.

It presents crisp clear the boundaries where the given surface is 2. Outside the inequality is true, inside it is false.

A good idea is to approximate or the this boundary curve set.

Answer 2

Conjectures :

Using the comment above and the fact that $r(x)$ increases along the positive real axis we have the first conjecture :

Let $x>0$ then we have :

$$x\cdot r\left(\left(\frac{4x^{2}}{\left(x+2\right)^{2}}\right)^{\frac{-1}{x}}\left(x-\sqrt{\frac{4x^{2}}{\left(x+2\right)^{2}}}\right)^{-1}\right)\geq 2$$

After that we have a second conjecture :

Let $0<x<1$ then $\exists a>1$,$\exists b\in R^{*}$ and $|b|<x$ and $x+a\geq 2$ such that :

$=\left(\left(a-b\right)\left(x+b\right)\right)^{\frac{-1}{x+a}}\left(x+a-\sqrt{\left(x+b\right)\left(a-b\right)}\right)^{-1}\leq \left(ax\right)^{-\frac{1}{x+a}}x^{-\frac{x}{x+a}}a^{-\frac{a}{x+a}}$

This two conjecture are sufficient to show the proposed problem .

Edit :

For the first conjecture and using Bernoulli's inequality we need to show for $x\geq 1$ :

$$x\cdot r\left(\left(1+\frac{1}{x}\left(\frac{4x^{2}}{\left(x+2\right)^{2}}-1\right)\right)^{-1}\left(x-\sqrt{\frac{4x^{2}}{\left(x+2\right)^{2}}}\right)^{-1}\right)\geq 2$$

This last inequality could also be seen as a long polynomial with a root at $x=2$

Edit 2 :

For the second conjecture we can use derivative with respect to $b$ see Wolfram alpha

Edit 3 :

Due to the homogeneity in the second conjecture we can choose :

$$b=a-\frac{a^2}{x}$$

We obtain a one variable inequality with the contraint of the second conjecture .

Last edit :

Unfortunetaly the second conjecture is not sufficient but I propose another conjecture wich seems highly true :

Let $0<a\leq 1$ and $x\geq 1$ such that $2\leq a+x\leq 5$ then we have :

$$g\left(x+a\right)-f\left(x\right)\leq 0$$

Where :

$$f(x)=\left(x+a\right)\cdot r\left(\left(ax\right)^{-\frac{1}{x+a}}x^{-\frac{x}{x+a}}a^{-\frac{a}{x+a}}\right)$$

And :

$$g\left(x\right)=x\cdot r\left(\left(1+\frac{1}{x}\left(\frac{4x^{2}}{\left(x+2\right)^{2}}-1\right)\right)^{-1}\left(x-\sqrt{\frac{4x^{2}}{\left(x+2\right)^{2}}}\right)^{-1}\right)$$

In other word we ensure the inequality including the minimum .