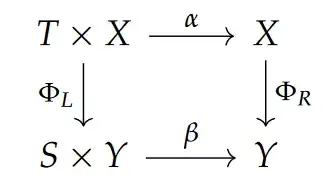The dynamics perspective on conjugacy is that it's a change of coordinates; see e.g. What is the relationship between the vector fields of conjugate flows?, Topological Invariance of Unique Ergodicity and The Horizontal Flow, The Time-One Map, $C^r$ conjugation and Suspension of a Diffeomorphism for instantiations of this idea. My answer in How a group represents the passage of time? is also relevant. In dynamics and ergodic theory, the problem of conjugacy in fact can be considered to be the major open problem; here is an excerpt from Halmos' Lectures on Ergodic Theory (pp.96-97):

See also the talk by B. Weiss "The unsolved problems of Halmos" (https://youtu.be/pvOqI65etMc).
Regarding interesting examples, below I present two classical examples from hyperbolic dynamics.
Let $M$ be a compact $C^\infty$ manifold, $f:M\to M$ be a $C^1$ diffeomorphism of it. $f$ is called Anosov (or (uniformly) hyperbolic) if there is an invariant splitting $TM=S(f)\oplus U(f)$ such that $Tf$ contracts vectors in $S(f)$ exponentially fast and $Tf^{-1}$ contracts vectors in $U(f)$ exponentially fast with respect to some (hence any) $C^0$ fiberwise norm (see What is the constant of hyperbolicity?, A question on hyperbolic toral automorphism for details).
Next denote by $\mathbb{T}^d=\mathbb{R}^d/\mathbb{Z}^d$ the $d$-dimensional torus. $\mathbb{T}^d$ is a compact Lie group (in particular it's a $C^\infty$ manifold), and Lie group automorphisms of it can be identified with the group $\operatorname{GL}(d,\mathbb{Z})$ of invertible $d\times d$ matrices with integer entries whose inverse is also with integer entries (see Endomorphisms of the Torus); they are in particular also $C^1$ diffeomorphisms. A Lie group automorphism of $\mathbb{T}^d$ is called hyperbolic if as a linear operator it has no eigenvalues of modulus $1$ (see Space of linear, continuous, hyperbolic functions is open, dense in the set of invertible functions). Thus hyperbolic Lie group automorphisms of the torus $\mathbb{T}^d$ are special examples of Anosov diffeomorphisms; the stable subbundle corresponds to (translations of) the direct sum of generalized eigenspaces corresponding to eigenvalues of modulus less than $1$ and the unstable subbundle corresponds to (translations of) the direct sum of generalized eigenspaces coresponding to eigenvalues of modulus greater than $1$.
If $M$ and $N$ are two topological spaces and $f:M\to M$ and $g:N\to N$ are two homeomorphisms, call $f$ and $g$ topologically conjugate if there is a homeomorphism $\Phi:M\to N$ such that $g=\Phi\circ f\circ \Phi^{-1}$. (Note that the conjugacies Halmos is considering in the above excerpt are in the category of standard probability spaces.)
Theorem (Franks-Manning): Let $f:\mathbb{T}^d\to \mathbb{T}^d$ be a $C^1$ diffeomorphism. If $f$ is Anosov then it is topologically conjugate to a hyperbolic Lie group automorphism of $\mathbb{T}^d$.
Theorem (Franks-Newhouse): Let $M$ be a compact $C^\infty$ manifold of dimension $d$ and let $f:M\to M$ be a $C^1$ diffeomorphism. If $f$ is Anosov and either the stable bundle $S(f)$ or the unstable bundle $U(f)$ is of rank $1$, then $f$ is topologically conjugate to a hyperbolic Lie group automorphism of $\mathbb{T}^d$.
Corollary: The only compact surface that carries an Anosov diffeomorphism is $\mathbb{T}^2$ (and the only such Anosov diffeomorphisms are induced by hyperbolic matrices, up to topological coordinate change).
For further details and references see e.g. Mañé's Ergodic Theory and Differentiable Dynamics.
Regarding unification, a categorical language could be a good start. Here is a very rough outline (somewhat in jest) (I'm building on my answer in How a group represents the passage of time?): Let $\mathscr{C}$ be a category that admits binary products (e.g. the category of measurable spaces with measurable maps, or the category of standard measure spaces with measure preserving measurable maps, or the category of metric spaces with continuous maps, or the category of $C^r$ manifolds with $C^r$ maps, or the category of Lie groups and Lie group homomorphisms,...). Denote by $\operatorname{DS}(\mathscr{C})$ the category whose objects are triples $(X,T,\alpha)$, where $X$ and $T$ are objects and $\alpha: T\times X\to X$ is an arrow in $\mathscr{C}$; and whose arrows are pairs of arrows $\Phi=(\Phi_L,\Phi_R): (X,T,\alpha)\to (Y,S,\beta)$ such that $\Phi_R\circ \alpha=\beta\circ \Phi_L$:
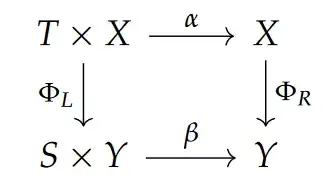
Let's call $\operatorname{DS}(\mathscr{C})$ the (nonautonomous) dynamical system object category associated to $\mathscr{C}$. One can consider subcategories of $\operatorname{DS}(\mathscr{C})$ with various further restrictions, e.g.
$\Phi_L:T\times X\to S\times Y$ splits as $(t,x)\mapsto (\Phi_{LL}(t,x),\Phi_{LR}(x))$, in which case $\Phi_{LL}: T\times X\to S$ would be called a time change.
$\Phi_L:T\times X\to S\times Y$ splits as $(t,x)\mapsto (\Phi_{LL}(t),\Phi_{LR}(x))$, in which case $\Phi_{LL}: T\to S$ would be called a constant time change.
$T=S$ and $\Phi_L:T\times X\to T\times Y$ is of the form $(t,x)\mapsto (t,\Phi_{LR}(x))$.
Any one of the previous three options, with the additional requirement that $\Phi_{LR}=\Phi_R$.
If in addition there is a well-defined associated group object category $\operatorname{Grp} (\mathscr{C})$ (for all examples for $\mathscr{C}$ I gave above this is valid) one can consider the full subcategory defined by the requirement $T$ is an object in $\operatorname{Grp} (\mathscr{C})$.
If in addition there is a well-defined associated group object category $\operatorname{Grp}(\mathscr{C})$ one can require $\alpha$ be a group action.
In all example categories I've listed we have $\mathbb{Z}\in \operatorname{Grp} (\mathscr{C})$; the subcategory of $\operatorname{DS}(\mathscr{C})$ cut out by options 3, 4 and 6 combined with $T=\mathbb{Z}$ recovers "semi-conjugacy" as used in dynamics and ergodic theory. In this case $\alpha$ is determined by $\alpha(1,\bullet)$, whence this subcategory is isomorphic (though not naturally) to the category $\operatorname{Con}(\mathscr{C})$ whose objects are isomorphisms in $\mathscr{C}$ and whose arrows $\Phi: [f:X\to X]\to [g:Y\to Y]$ are arrows $\Phi: X\to Y$ in $\mathscr{C}$ such that $\Phi\circ f=g\circ \Phi$.
(Under some self-referentiality assumptions if needed, one can consider $\operatorname{DS}(\mathscr{C})$ itself as an $X$ and talk about "higher dynamical systems" similar to cellular automata etc.)
To connect this formalism to your group theory example, note that any group can be considered as a category $\mathscr{G}$ with exactly one object and all arrows isomorphisms (see Group as a category). $\mathscr{G}$ does not admit binary products (let alone a group object category), however $\operatorname{Con}(\mathscr{G})$ still makes sense. Similarly one can consider $\operatorname{Con}(\mathscr{M})$ for $\mathscr{M}$ a monoid considered as a category; this recovers your linear algebra example (though one can interpret this within the non-categorical framework as linear conjugacy of linear maps as well, as you've remarked; in this context Kuiper & Robbin's paper "Topological classification of linear endomorphisms" might be worth a look, where topological conjugacy of linear maps is considered).
As a final disclaimer, this structuralist approach can be misleading; the dynamical systems most dynamicists are interested in classifying have often subtler properties that this formalism ignores (which is why this part is in jest).