What do you mean by normal form?
Note that the statement is that any $2\times 2$ matrix is one of the listed matrices up to conjugacy, that is to say, linear coordinate change (in this context; see Examples of conjugate-like structures across mathematics for conjugacies in broader senses). The listed matrices are the paradigmatic ones in a sense; "normal form" simply indicates this. See the discussion at What is a local normal form? for more.
Why can this be verified using the exponential matrix?
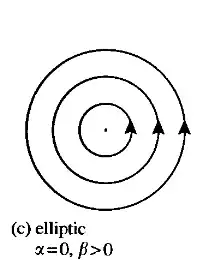
Thinking of a $2\times 2$ matrix $A$ as a linear vector field on the plane, the exponential $\exp(tA)$ of its $t$ scalar multiple dictates the associated linear flow. Thus if one has an explicit expression for $\exp(tA)$, then given an anonymous initial condition $v=(x,y)$, one can consider the function $t\mapsto\exp(tA)(x,y)^T$ and the graph of this function would be the trajectory of the point starting at $v$. E.g. in the example you are considering if the initial condition is $v=(1,0)$, then the trajectory of $v$ is $(\cos(t),\sin(t))$, that is, a circle centered at the origin (of course the exponential encodes information about the speed also); using different initial conditions gives a more complete phase portrait. Conversely the fact that the phase portrait seems to be concentric circles is justification for the vector field being given by an elliptic matrix (at least when one considers normal forms; indeed perhaps the diagram given is with respect to some unknown (but linear) coordinate system).