I am studying dynamical systems of discrete time, and I am having some trouble in understanding what is the constant of hyperbolicity for a closed hyperbolic set $\Lambda \in M$ of a diffeomorphism $f:M\rightarrow M$, where $M$ is a compact differentiable manifold.
-
1It would be helpful if you state the definition you're using and what parts of it you're having trouble understanding. – Kajelad May 02 '22 at 03:09
-
In fact an exact reference would be better, though from the context it seems the constant is an exponential rate with which infinitesimally close orbit converge or diverge from one another. – Alp Uzman May 02 '22 at 06:25
-
Related: https://math.stackexchange.com/q/4126880/169085 – Alp Uzman May 02 '22 at 08:06
1 Answers
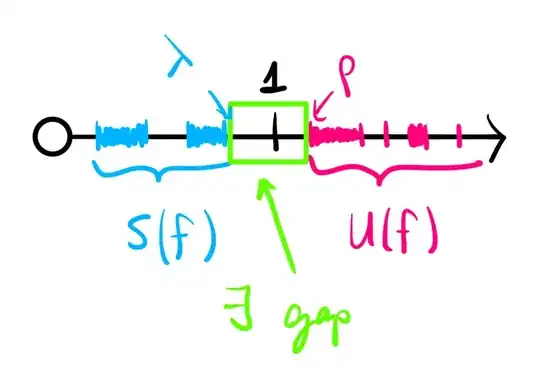
Say the closed subset $\Lambda\subseteq M$ is $f$-invariant and (uniformly) $f$-hyperbolic, so that there is a continuous splitting $T_\Lambda M=S(f)\oplus U(f)$ and for some fixed $C^0$ Riemannian metric on $M$ there two numbers $(\lambda,\rho)\in\mathbb{R}_{>0}^2$ with $\lambda <1 <\rho$ and another number $C\in\mathbb{R}_{>0}$ such that for any $x\in \Lambda$ and for any $n\in\mathbb{Z}_{\geq0}$:
$$\forall v\in S_x(f)\setminus0: |T_xf^n v|_{f^n(x)}\leq C \lambda^n |v|_x \text{ and }$$
$$\forall v\in U_x(f)\setminus0: |T_xf^{-n} v|_{f^{-n}(x)}\leq C \rho^{-n} |v|_x,$$
then the constant of hyperbolicity for $f:\Lambda\to \Lambda$ is either $\lambda$, or $\rho$, or some other number $\kappa\in\mathbb{R}_{>0}$ such that $\lambda\leq\kappa<1<\kappa^{-1}\leq\rho$ (e.g. if you are following Shub's Global Stability of Dynamical Systems (p.82) (or Pilyugin's The Space of Dynamical Systems with the $C^0$-Topology (p.62)).
In ODE theory this situation is sometimes referred to as an exponential $(\lambda,\rho)$-dichotomy. The actual numbers become important when it comes to subtle estimates (or more sophisticated versions of hyperbolicity), but roughly the idea is that that there are such constants guarantees a good separation of vectors that correspond to infinitesimally different behaviors; any vector approximates arbitrarily well either a vector in the stable subbundle or the unstable subbundle if enough time passes. This provides a robust theory (e.g. in the definition above one doesn't need to assume that the splitting is continuous; in fact not only is it continuous but Hölder continuous). I personally find the "Mather diagram" very useful to keep track of such numbers, such a diagram looks like this:
(What this is is really the spectrum, up to rotation, of the adjoint operator of $f$ acting on the space of continuous vector fields; $X\mapsto Tf\circ X\circ f^{-1}$.)
As a suggestive example, one can consider an invertible $2\times 2$ matrix $A$ with both eigenvalues real and modulus different than $1$. (Also see Space of linear, continuous, hyperbolic functions is open, dense in the set of invertible functions for a related discussion.)
- 10,742